40 Of 320
interactiveleap
Sep 19, 2025 · 5 min read
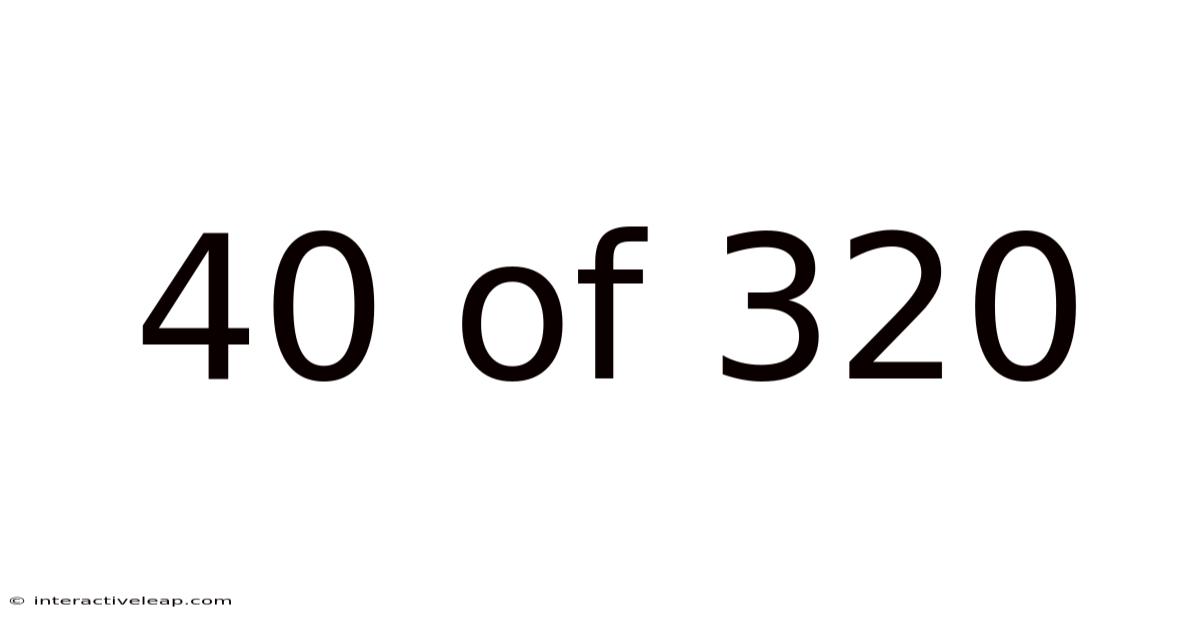
Table of Contents
Decoding the Enigma: Understanding the Fraction 40/320 and its Implications
The seemingly simple fraction 40/320 might appear straightforward at first glance. However, understanding its implications goes beyond simple arithmetic. This article will delve into the various aspects of this fraction, exploring its simplification, its decimal equivalent, its percentage representation, and its applications in real-world scenarios. We'll also examine its relationship to ratios and proportions, offering a comprehensive understanding for students, educators, and anyone curious about the power hidden within this seemingly insignificant fraction.
I. Simplifying the Fraction 40/320
The first step in understanding 40/320 is to simplify it to its lowest terms. This process involves finding the greatest common divisor (GCD) of both the numerator (40) and the denominator (320). The GCD is the largest number that divides both 40 and 320 without leaving a remainder.
To find the GCD, we can use several methods. One common method is prime factorization. Let's break down both numbers into their prime factors:
- 40 = 2 x 2 x 2 x 5 = 2³ x 5
- 320 = 2 x 2 x 2 x 2 x 2 x 2 x 5 = 2⁶ x 5
The common factors are 2³ and 5. Therefore, the GCD is 2³ x 5 = 40.
Dividing both the numerator and the denominator by the GCD (40), we get:
40 ÷ 40 / 320 ÷ 40 = 1/8
Therefore, the simplified form of the fraction 40/320 is 1/8. This simplified form is crucial for easier calculations and a clearer understanding of the fraction's value.
II. Decimal and Percentage Equivalents
Converting fractions to decimals and percentages is a fundamental skill in mathematics. Let's convert 1/8 (the simplified form of 40/320) to its decimal and percentage equivalents.
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
1 ÷ 8 = 0.125
Therefore, the decimal equivalent of 40/320 is 0.125.
To convert a decimal to a percentage, we multiply by 100:
0.125 x 100 = 12.5%
Thus, the percentage equivalent of 40/320 is 12.5%. This representation is particularly useful for visualizing proportions and making comparisons.
III. Real-World Applications: Understanding Proportions and Ratios
The fraction 40/320, or its simplified form 1/8, has numerous applications in real-world scenarios. Understanding its implications involves grasping the concept of proportions and ratios.
-
Example 1: Survey Results: Imagine a survey where 40 out of 320 respondents answered "yes" to a particular question. The fraction 40/320 represents the proportion of "yes" responses. Simplifying to 1/8 shows that 1 out of every 8 respondents answered "yes." This information is valuable for analyzing survey data and drawing conclusions.
-
Example 2: Recipe Scaling: Suppose a recipe calls for 40 grams of sugar for a batch that yields 320 cookies. The fraction 40/320 (or 1/8) represents the ratio of sugar to cookies. To make a smaller batch of, say, 80 cookies, you would need to adjust the sugar accordingly. Using the ratio, you would need 10 grams of sugar (80 cookies x (1/8) sugar).
-
Example 3: Financial Calculations: Imagine a company's profit is $40 million out of a total revenue of $320 million. The fraction 40/320 (or 1/8) represents the company's profit margin. This percentage (12.5%) provides a crucial indicator of the company's financial health.
-
Example 4: Probability: In a scenario with 320 equally likely outcomes, where 40 outcomes represent a specific event, the probability of that event occurring is 40/320, or 1/8. This is a fundamental concept in probability theory.
IV. Expanding the Understanding: Beyond Simple Calculations
While simplifying, converting to decimals and percentages, and applying the fraction to real-world problems are crucial, it's important to further enhance our understanding of 40/320.
-
Relationship to other fractions: The fraction 1/8 is closely related to other common fractions like 1/4 (which is double 1/8) and 1/2 (which is four times 1/8). Understanding these relationships helps build a stronger intuition for fractions and their magnitudes.
-
Visual Representations: Visual aids such as pie charts, bar graphs, and fraction circles can effectively illustrate the fraction 1/8. This helps in grasping the magnitude of the fraction more intuitively, especially for visual learners.
-
Comparative Analysis: Comparing 40/320 to other fractions can provide insights into relative magnitudes. For instance, comparing it to 1/4 or 1/10 helps to understand its position within the range of fractions.
V. Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 40/320?
- A: The simplest form is 1/8.
-
Q: How do I convert 40/320 to a decimal?
- A: Divide the numerator (40) by the denominator (320). This gives 0.125.
-
Q: What is the percentage equivalent of 40/320?
- A: Multiply the decimal equivalent (0.125) by 100 to get 12.5%.
-
Q: Are there any real-world applications of this fraction?
- A: Yes, numerous applications exist, such as representing proportions in surveys, ratios in recipes, profit margins in finance, and probabilities in various scenarios.
-
Q: How can I visually represent the fraction 1/8?
- A: You can use a pie chart divided into 8 equal slices, shading one slice to represent 1/8. You could also use a bar graph or fraction circles.
VI. Conclusion: The Significance of Understanding Fractions
The fraction 40/320, while seemingly insignificant at first, offers a valuable opportunity to explore fundamental mathematical concepts. Understanding its simplification, decimal and percentage equivalents, and its application in real-world scenarios provides a solid foundation for more advanced mathematical studies. Mastering these concepts builds confidence and problem-solving skills, essential for success in various academic and professional fields. The seemingly simple act of understanding a fraction like 40/320 highlights the power of mathematical literacy and its role in navigating the complexities of the world around us. Remember, every number, every fraction, holds a story – and understanding that story unlocks deeper understanding and empowers us to tackle increasingly complex challenges. The journey from 40/320 to 1/8 is not just a mathematical simplification; it's a journey of understanding, application, and empowerment.
Latest Posts
Latest Posts
-
70 Of 14
Sep 19, 2025
-
80 Of 16
Sep 19, 2025
-
70 Of 170
Sep 19, 2025
-
60 Of 1200
Sep 19, 2025
-
30 Of 450
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 320 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.