30 Of 450
interactiveleap
Sep 19, 2025 · 5 min read
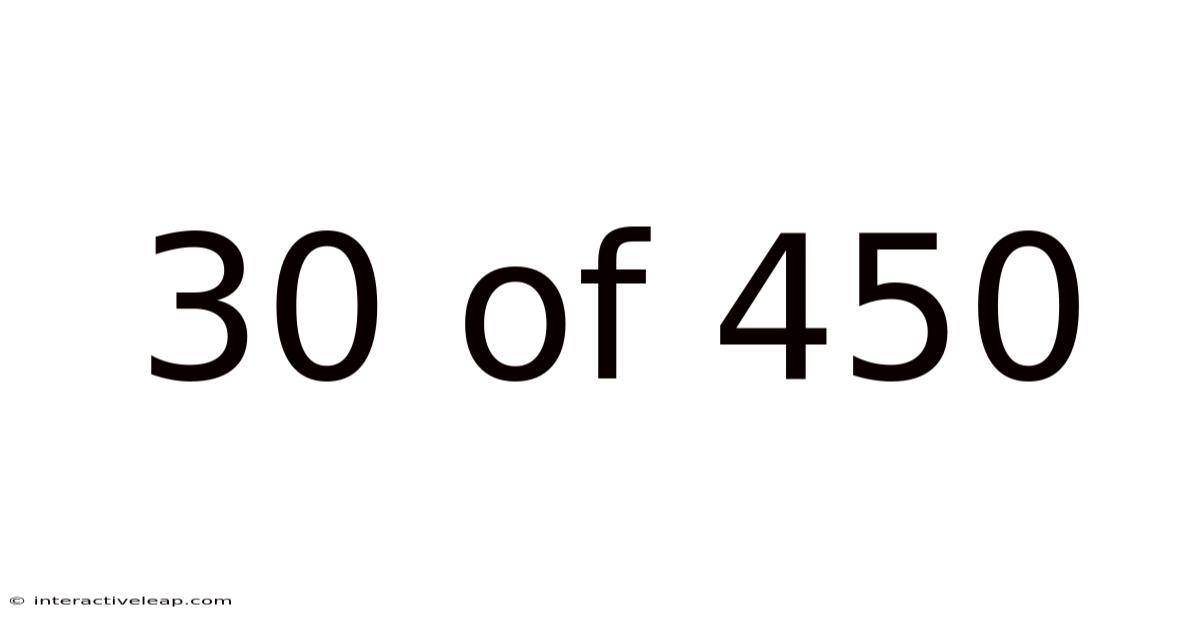
Table of Contents
Decoding the Fraction: Understanding the Significance of 30 out of 450
The seemingly simple fraction 30 out of 450 – or 30/450 – represents more than just a numerical value. It's a gateway to understanding ratios, percentages, proportions, and their applications in various fields. This article delves deep into the meaning of this fraction, exploring its mathematical representation, practical interpretations, and how to approach similar problems. Whether you're a student grappling with fractions, a professional analyzing data, or simply someone curious about the mathematical world, this comprehensive guide will illuminate the significance of 30 out of 450 and empower you to confidently tackle similar scenarios.
Simplifying the Fraction: From Complex to Concise
The first step in understanding 30/450 is to simplify it. Simplification involves finding the greatest common divisor (GCD) of the numerator (30) and the denominator (450) and dividing both by it. The GCD of 30 and 450 is 30. Therefore:
30 ÷ 30 = 1 450 ÷ 30 = 15
This simplifies the fraction to its simplest form: 1/15. This simplified fraction is mathematically equivalent to 30/450, meaning they represent the same proportion or ratio. Working with the simplified fraction makes calculations and interpretations much easier.
Representing the Fraction: Different Perspectives
The fraction 30/450, or its simplified form 1/15, can be represented in several ways, each offering a unique perspective:
-
Decimal: Dividing 1 by 15 gives us the decimal equivalent of approximately 0.0667. This representation is useful for calculations involving decimals and comparisons with other decimal values.
-
Percentage: To express the fraction as a percentage, we multiply the decimal value by 100. Therefore, 1/15 is approximately 6.67%. The percentage representation provides a clear and concise way to visualize the proportion relative to the whole.
-
Ratio: The fraction can also be expressed as a ratio: 1:15. This representation emphasizes the relationship between the two quantities – one part for every fifteen parts.
Choosing the appropriate representation depends on the context and the type of analysis required.
Real-World Applications: Contextualizing the Fraction
Understanding the practical implications of 30/450 requires contextualizing it within a real-world scenario. Let’s explore a few examples:
Example 1: Test Scores
Imagine a student scored 30 out of 450 on a test. This means they answered 30 questions correctly out of a total of 450 questions. The simplified fraction 1/15, or 6.67%, represents their performance. This low percentage indicates a need for improvement.
Example 2: Survey Results
In a survey of 450 people, 30 responded positively to a particular question. The fraction 30/450 (or 1/15) represents the proportion of respondents with positive feedback. This data is crucial for understanding public opinion.
Example 3: Inventory Management
A warehouse has 450 units of a particular product, and 30 are damaged. The fraction 30/450 (or 1/15) represents the proportion of damaged goods. This information is essential for inventory control and loss calculations.
Example 4: Manufacturing Defects
A manufacturing plant produces 450 items, and 30 are defective. The fraction 30/450 signifies the defect rate. This data is critical for quality control and process improvement.
These examples demonstrate the versatility of the fraction 30/450. The key is to understand the context to interpret the meaning and significance of this proportion correctly.
Extending the Understanding: Proportions and Ratios
The fraction 30/450 is fundamentally a ratio, comparing two quantities. Understanding proportions is crucial for extending this understanding. A proportion states that two ratios are equal. For instance:
30/450 = x/100
Solving for 'x' allows us to find the equivalent proportion out of 100, which easily converts to a percentage. In this case, x = 6.67, representing 6.67%. This highlights the interconnectedness between fractions, ratios, and percentages.
Dealing with Larger Numbers: Maintaining Accuracy
When dealing with larger numbers, it's crucial to maintain accuracy throughout calculations. Using a calculator or spreadsheet software can minimize errors, particularly when dealing with decimals and percentages. Rounding off to appropriate significant figures is also essential to avoid unnecessary precision.
Beyond the Basics: Advanced Applications
The concept extends beyond simple calculations. It is essential in various fields such as:
- Finance: Calculating interest rates, returns on investment, and risk assessments.
- Statistics: Determining probabilities, analyzing data distributions, and conducting statistical tests.
- Science: Measuring concentrations, analyzing experimental data, and developing scientific models.
- Engineering: Designing structures, calculating material requirements, and evaluating system performance.
Frequently Asked Questions (FAQ)
Q1: How do I convert 30/450 to a percentage?
A1: First, simplify the fraction to 1/15. Then, divide 1 by 15 to get the decimal equivalent (approximately 0.0667). Finally, multiply the decimal by 100 to get the percentage (approximately 6.67%).
Q2: What is the greatest common divisor (GCD) of 30 and 450?
A2: The GCD of 30 and 450 is 30.
Q3: Can I use a calculator to solve these problems?
A3: Yes, calculators are very helpful, especially for complex fractions and conversions. Make sure to use a calculator that allows for fraction simplification.
Q4: Why is simplifying a fraction important?
A4: Simplifying makes the fraction easier to understand and work with. It reduces the numbers involved, making calculations simpler and reducing the risk of errors.
Q5: How can I apply this knowledge in my daily life?
A5: Understanding fractions and percentages is vital for everyday tasks such as budgeting, shopping, calculating discounts, understanding statistics in news reports, and interpreting data in many different contexts.
Conclusion: Mastering the Power of Proportion
The seemingly simple fraction 30/450, once simplified to 1/15, reveals a wealth of mathematical concepts. Understanding its representation as a decimal, percentage, and ratio allows for a versatile application across numerous fields. By grasping the underlying principles of ratios and proportions, we unlock the power to analyze data, solve problems, and make informed decisions in various real-world scenarios. Remember that the core concept lies in understanding the proportional relationship between the parts and the whole, a fundamental concept that transcends the specific numerical values involved. This foundational understanding forms the base for more complex mathematical concepts and has far-reaching applications in numerous disciplines. Mastering the intricacies of 30/450 lays the groundwork for a deeper understanding of the mathematical world around us.
Latest Posts
Latest Posts
-
Is Hell Profanity
Sep 19, 2025
-
5 12 As Decimal
Sep 19, 2025
-
60 Of 205
Sep 19, 2025
-
Farm En Espanol
Sep 19, 2025
-
85 Of 240
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 30 Of 450 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.