85 Of 240
interactiveleap
Sep 19, 2025 · 6 min read
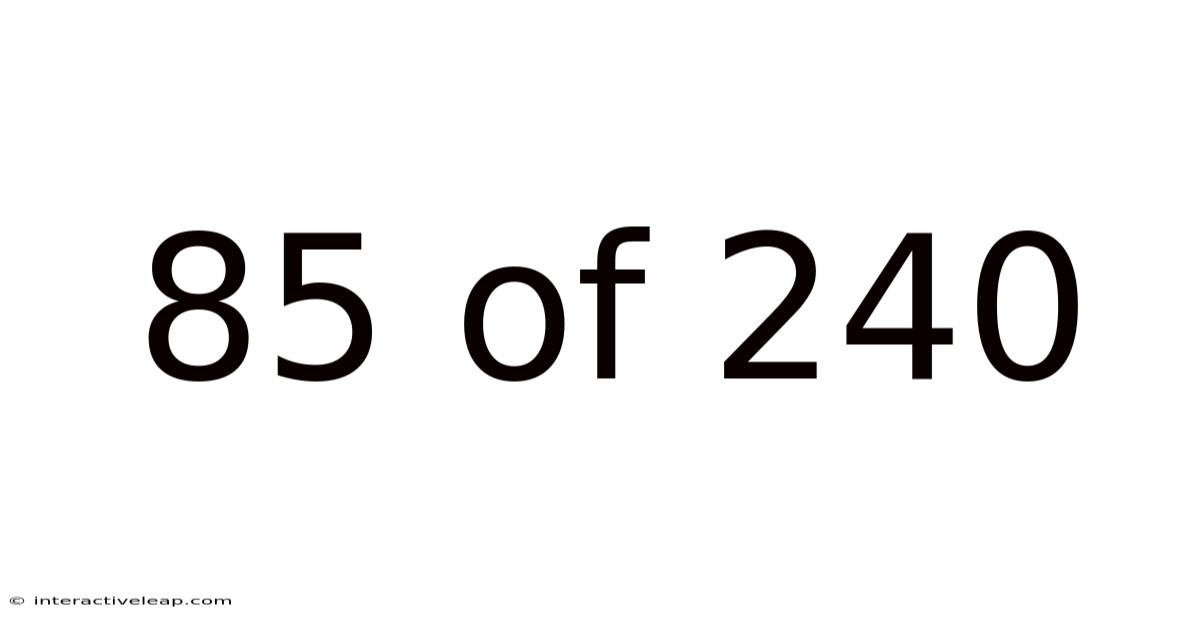
Table of Contents
Decoding 85/240: Understanding Fractions, Percentages, and Their Applications
Understanding fractions and percentages is fundamental to many areas of life, from everyday budgeting to advanced scientific calculations. This article will delve into the meaning of 85/240, exploring how to simplify it, convert it to a percentage and decimal, and ultimately, understanding its practical applications. We'll also explore the broader context of fraction and percentage manipulation, equipping you with the tools to tackle similar problems with confidence.
Introduction: What Does 85/240 Represent?
The fraction 85/240 represents a part of a whole. The number 85 is the numerator (the part), and 240 is the denominator (the whole). This means we have 85 units out of a possible 240 units. Imagine you have 240 apples, and you've already eaten 85. 85/240 represents the portion of apples you've consumed. This seemingly simple fraction can be understood and applied in numerous ways, which we will explore in detail. This article will cover simplifying fractions, converting fractions to percentages and decimals, and exploring real-world applications of such calculations. Understanding the concepts behind 85/240 will provide a solid foundation for tackling more complex mathematical problems.
1. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we convert 85/240 to a percentage or decimal, it's essential to simplify the fraction. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). Finding the GCD can be done using various methods, including:
-
Listing Factors: List all the factors of both 85 and 240. The largest number that appears in both lists is the GCD.
- Factors of 85: 1, 5, 17, 85
- Factors of 240: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240
The GCD of 85 and 240 is 5.
-
Prime Factorization: Break down both numbers into their prime factors. The GCD is the product of the common prime factors raised to the lowest power.
- 85 = 5 x 17
- 240 = 2<sup>4</sup> x 3 x 5
The only common prime factor is 5. Therefore, the GCD is 5.
Now, we divide both the numerator and denominator by the GCD (5):
85 ÷ 5 = 17 240 ÷ 5 = 48
Therefore, the simplified fraction is 17/48. This simplified fraction is equivalent to 85/240, but it's easier to work with.
2. Converting the Fraction to a Decimal:
Converting a fraction to a decimal involves dividing the numerator by the denominator. Using our simplified fraction 17/48:
17 ÷ 48 ≈ 0.3542
Therefore, the decimal equivalent of 85/240 is approximately 0.3542.
3. Converting the Fraction to a Percentage:
To convert a fraction to a percentage, we first convert it to a decimal (as shown above) and then multiply by 100%.
0.3542 x 100% ≈ 35.42%
Therefore, 85/240 is approximately 35.42%. This means that 85 is approximately 35.42% of 240.
4. Real-World Applications of 85/240 and Similar Calculations:
The ability to understand and manipulate fractions and percentages is crucial in various real-world scenarios. Here are some examples:
-
Grade Calculation: Imagine a student scored 85 out of 240 points on a test. Understanding 85/240 allows them to calculate their percentage score (approximately 35.42%), providing a clear understanding of their performance.
-
Sales and Discounts: A store might offer a discount of 85 out of every 240 items sold. Calculating the percentage discount helps customers understand the savings.
-
Project Completion: If a project has 240 tasks, and 85 are completed, calculating the percentage of completion (35.42%) provides a clear picture of the project's progress.
-
Statistical Analysis: In data analysis, fractions and percentages are used extensively to represent proportions and probabilities. 85/240 might represent the proportion of a specific characteristic within a larger dataset.
-
Financial Management: Budgeting, calculating interest rates, understanding investment returns, and analyzing financial statements all heavily rely on the ability to work with fractions and percentages. For example, if a company's profit is 85 out of every 240 dollars of revenue, it reveals the profit margin.
-
Recipe Scaling: Adjusting the quantities of ingredients in a recipe involves working with fractions. If a recipe calls for 85 grams of flour for 240 cookies, you can easily scale the recipe up or down using this knowledge.
5. Further Exploration: Working with Fractions and Percentages
Beyond 85/240, understanding the broader principles of fraction and percentage manipulation is essential. Here are some key concepts to consider:
-
Adding and Subtracting Fractions: This requires finding a common denominator.
-
Multiplying and Dividing Fractions: This involves multiplying numerators and denominators separately (or inverting the second fraction for division).
-
Converting Between Fractions, Decimals, and Percentages: The ability to fluently switch between these representations is vital for solving various problems.
-
Working with Percentages: Understanding how to calculate percentage increases and decreases, percentage points, and percentage change is important for practical applications.
-
Ratio and Proportion: Fractions are closely related to ratios, and understanding proportions is key to solving problems involving equivalent fractions and scaling.
6. Frequently Asked Questions (FAQ)
-
Q: How do I know if a fraction is in its simplest form?
- A: A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1.
-
Q: What if I get a repeating decimal when converting a fraction?
- A: Some fractions produce repeating decimals (e.g., 1/3 = 0.333...). You can either round the decimal to a certain number of places or express it using a bar notation (e.g., 0.3̅).
-
Q: Are there any online calculators or tools to help with fraction and percentage calculations?
- A: Yes, many online calculators are available to simplify fractions, convert between fractions, decimals, and percentages, and perform various other calculations. However, understanding the underlying principles is crucial for problem-solving skills.
7. Conclusion: Mastering Fractions and Percentages
The seemingly simple fraction 85/240 provides a valuable opportunity to understand fundamental mathematical concepts. By simplifying the fraction, converting it to a decimal and percentage, and exploring its various applications, we've gained a deeper appreciation for the practical importance of fractions and percentages in everyday life. Mastering these concepts is crucial for success in various fields and enhances problem-solving abilities. This article has provided a comprehensive guide to understanding 85/240, but remember that the true benefit comes from practicing these principles in various contexts and further developing your skills in fraction and percentage manipulation. The more you practice, the more confident and proficient you will become in tackling similar problems independently.
Latest Posts
Latest Posts
-
How Draw Landscape
Sep 19, 2025
-
8 Metres Squared
Sep 19, 2025
-
Half Of 120
Sep 19, 2025
-
Beverly Polo Hills
Sep 19, 2025
-
0 7 X 0 5
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 85 Of 240 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.