0.7 X 0.5
interactiveleap
Sep 19, 2025 · 6 min read
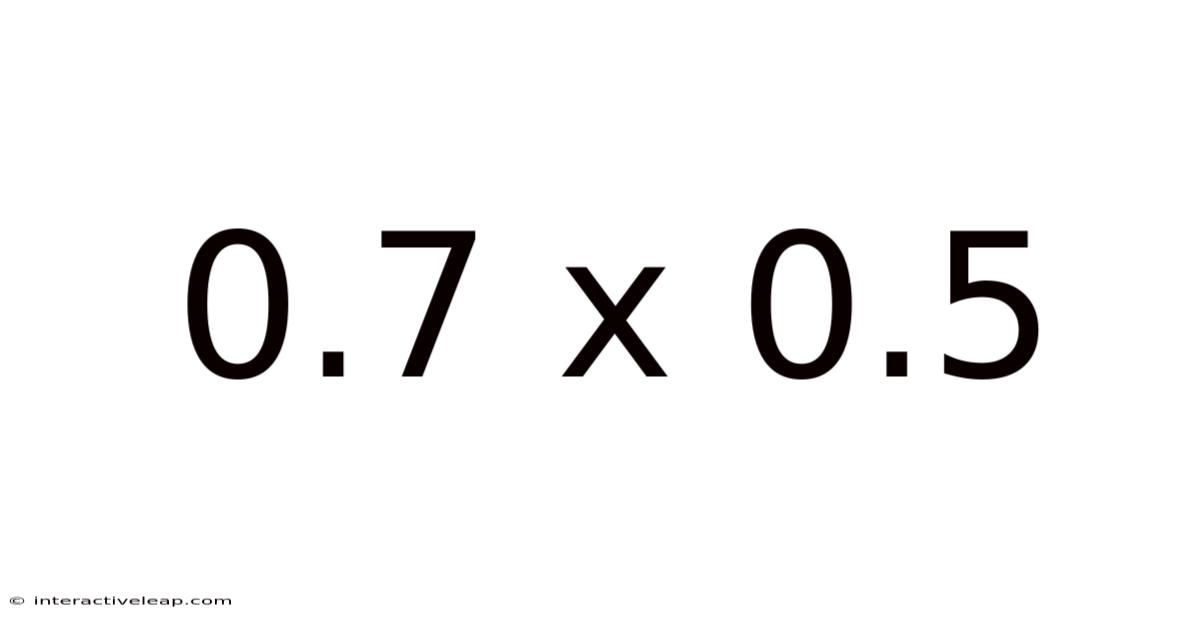
Table of Contents
Decoding 0.7 x 0.5: A Deep Dive into Decimal Multiplication
This article explores the seemingly simple multiplication problem of 0.7 x 0.5, unpacking it beyond a straightforward answer to reveal the underlying principles of decimal multiplication and its broader applications in mathematics and real-world scenarios. We'll cover the calculation itself, delve into the underlying mathematical concepts, examine different methods of solving the problem, and explore practical examples to solidify your understanding. This comprehensive guide will equip you with a robust understanding of decimal multiplication, empowering you to tackle more complex problems with confidence.
Understanding Decimal Numbers
Before diving into the multiplication, let's refresh our understanding of decimal numbers. Decimals are a way of representing numbers that are not whole numbers. They use a decimal point (.) to separate the whole number part from the fractional part. The digits to the right of the decimal point represent fractions of a whole, with each position representing a decreasing power of 10. For instance, in the number 0.7, the '7' represents seven-tenths (7/10), and in 0.5, the '5' represents five-tenths (5/10).
Method 1: Direct Multiplication
The most straightforward way to solve 0.7 x 0.5 is to perform the multiplication as if the numbers were whole numbers, then adjust the decimal point in the result.
-
Ignore the decimal points: Multiply 7 and 5: 7 x 5 = 35
-
Count the decimal places: In 0.7, there is one decimal place. In 0.5, there is also one decimal place. Together, there are two decimal places.
-
Place the decimal point: In the product (35), count two places from the right and insert the decimal point. This gives us 0.35.
Therefore, 0.7 x 0.5 = 0.35.
Method 2: Fraction Conversion
Decimals can be easily converted into fractions, providing an alternative method for multiplication.
-
Convert to fractions: 0.7 is equivalent to 7/10, and 0.5 is equivalent to 5/10.
-
Multiply the fractions: (7/10) x (5/10) = (7 x 5) / (10 x 10) = 35/100
-
Convert back to decimal: 35/100 is equivalent to 0.35.
This method reinforces the understanding that decimal multiplication is essentially fractional multiplication.
Method 3: Area Model (Visual Representation)
The area model provides a visual representation of multiplication, especially helpful for grasping the concept. Imagine a rectangle with sides of length 0.7 units and 0.5 units.
The area of this rectangle represents the product of the two numbers. We can visualize this rectangle as being part of a larger 1x1 square. The 0.7 side represents 7 tenths of the square's side length, and the 0.5 side represents 5 tenths. The area of the smaller rectangle would then represent 35 hundredths (35/100) of the larger square, which equals 0.35. This visual method is particularly beneficial for beginners as it provides an intuitive understanding of the process.
The Significance of Decimal Places
The number of decimal places in the result is crucial and directly relates to the number of decimal places in the original numbers. This principle holds true for all decimal multiplications. When multiplying decimals, the total number of decimal places in the product is the sum of the decimal places in each of the original numbers.
Applications of Decimal Multiplication in Real Life
Decimal multiplication isn't confined to textbooks; it's a fundamental tool in numerous real-world applications:
-
Finance: Calculating discounts (e.g., 0.7 x original price for a 30% discount), interest rates, and tax amounts.
-
Measurement: Determining areas and volumes using decimal measurements (e.g., calculating the area of a room with dimensions 0.7 meters by 0.5 meters).
-
Science: Many scientific calculations involve decimal numbers, especially in fields like physics and chemistry where precision is vital. Consider the calculation of speed, acceleration, or quantities of substances using decimal measurements.
-
Cooking and Baking: Recipes often utilize fractional measurements which translate directly to decimals. For example, adjusting a recipe by multiplying ingredient quantities by 0.7 or 0.5.
-
Engineering: Precise calculations in engineering, such as calculating load bearing capacities, require accurate multiplication of decimal numbers.
Expanding on Decimal Multiplication: More Complex Scenarios
While 0.7 x 0.5 provides a basic understanding, let's briefly explore more complex decimal multiplications:
-
Multiplying decimals with more decimal places: For instance, 0.75 x 0.52 involves a similar process; multiply the numbers as whole numbers (75 x 52 = 3900) and then count the total number of decimal places (two in 0.75 and two in 0.52, totaling four). Therefore, the answer is 0.3900 (or 0.39).
-
Multiplying decimals with whole numbers: Multiplying a decimal by a whole number involves adding zeros to the whole number as a placeholder, similar to multiplication using the decimal place adjustment method. For instance, 0.5 x 12. Treat it as 5 x 12 =60 and add the single decimal place to get 6.0 (or 6).
-
Multiplying multiple decimals: The process is analogous – multiply the numbers as whole numbers and then count the total number of decimal places to position the decimal point in the final answer. For example, 0.7 x 0.5 x 0.2 would result in 0.07.
Frequently Asked Questions (FAQ)
Q1: Why is the product of two numbers less than one (0.7 and 0.5) also less than one (0.35)?
A1: This is because you're multiplying fractions. Multiplying fractions always results in a smaller value unless one of the numbers is greater than one. Both 0.7 and 0.5 are less than 1, representing portions of a whole. Multiplying them together results in an even smaller portion of a whole.
Q2: Can I use a calculator to solve decimal multiplication problems?
A2: Absolutely! Calculators are efficient tools for solving decimal multiplication problems, especially for complex calculations. However, understanding the underlying principles is crucial for problem-solving and error checking.
Q3: Are there other methods for multiplying decimals besides the ones mentioned?
A3: Yes, there are other methods, including the use of logarithms, which are more advanced mathematical techniques. However, the methods discussed earlier (direct multiplication, fraction conversion, and the area model) are sufficient for most practical applications.
Q4: What if I make a mistake in positioning the decimal point?
A4: Incorrect decimal placement significantly alters the answer. Always double-check the number of decimal places in the original numbers and ensure the correct placement in the product.
Q5: What if I'm multiplying decimals with larger numbers of decimal places?
A5: The principle remains the same. Multiply as if the numbers were whole numbers, then count the total number of decimal places to accurately position the decimal point in the final answer. The process will remain consistent regardless of the number of decimal places involved.
Conclusion
The seemingly simple calculation 0.7 x 0.5 offers a gateway to understanding the broader concept of decimal multiplication. Through direct multiplication, fraction conversion, and the visual area model, we've explored several methods of solving this problem, highlighting the importance of understanding decimal place value. The real-world applications are vast, ranging from finance to science, underscoring the fundamental role of decimal multiplication in everyday life and specialized fields. Mastering this concept lays a strong foundation for tackling more complex mathematical problems and strengthens numerical reasoning skills applicable across numerous disciplines. Remember to practice consistently and use different methods to reinforce your understanding for improved accuracy and efficiency.
Latest Posts
Latest Posts
-
5 Century Bc
Sep 19, 2025
-
15 Of 27
Sep 19, 2025
-
4g In Mg
Sep 19, 2025
-
12 35 Simplified
Sep 19, 2025
-
6 2kg To Lbs
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 0.7 X 0.5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.