5/12 As Decimal
interactiveleap
Sep 19, 2025 · 6 min read
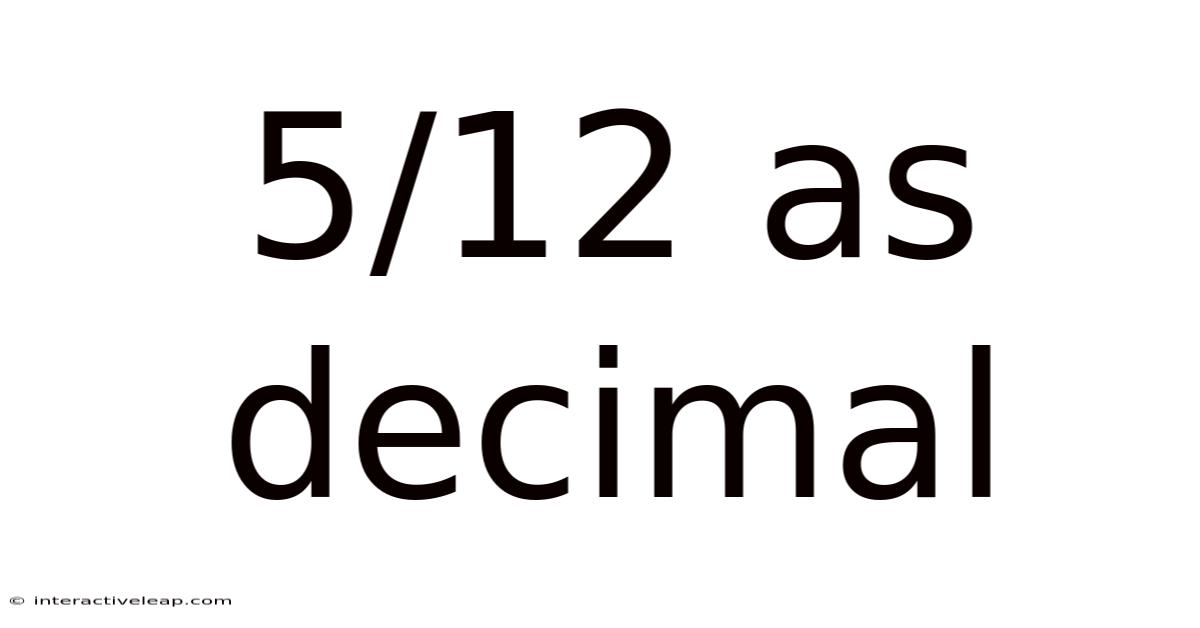
Table of Contents
Decoding 5/12 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the fraction 5/12 into its decimal form, providing a step-by-step process, explaining the underlying mathematical principles, and addressing common questions and misconceptions. We'll delve into various methods for performing the conversion, highlighting their strengths and weaknesses, and ultimately empower you with a solid understanding of this essential concept. This guide is perfect for students, educators, and anyone seeking to solidify their grasp on decimal representation of fractions.
Understanding Fractions and Decimals
Before we dive into the conversion of 5/12, let's briefly review the fundamental concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 5/12, 5 is the numerator and 12 is the denominator. This means we have 5 parts out of a total of 12 equal parts.
A decimal, on the other hand, represents a number using a base-10 system. The decimal point separates the whole number part from the fractional part. Each digit to the right of the decimal point represents a power of 10 (tenths, hundredths, thousandths, and so on). For example, 0.25 represents 2 tenths and 5 hundredths, or 25/100.
The process of converting a fraction to a decimal involves finding an equivalent representation of the fraction using a base-10 denominator. This can be achieved through several methods, which we will explore in the following sections.
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is through long division. We divide the numerator (5) by the denominator (12).
-
Set up the long division: Write the numerator (5) inside the long division symbol and the denominator (12) outside. Since 5 is smaller than 12, we add a decimal point and a zero to the numerator (making it 5.0).
-
Perform the division: 12 goes into 50 four times (12 x 4 = 48). Write the 4 above the decimal point and subtract 48 from 50, leaving a remainder of 2.
-
Add another zero: Bring down another zero to the remainder, making it 20.
-
Continue dividing: 12 goes into 20 one time (12 x 1 = 12). Write the 1 next to the 4 and subtract 12 from 20, leaving a remainder of 8.
-
Repeat the process: Bring down another zero to the remainder (making it 80). 12 goes into 80 six times (12 x 6 = 72). Write the 6 next to the 1 and subtract 72 from 80, leaving a remainder of 8.
-
Identify the repeating pattern: Notice that we keep getting a remainder of 8, and the division process will repeat indefinitely. This indicates a repeating decimal.
Therefore, 5/12 as a decimal is 0.416666..., which can be written as 0.416̅. The bar over the 6 signifies that the digit 6 repeats infinitely.
Method 2: Finding an Equivalent Fraction with a Power of 10 Denominator
While long division is a reliable method, it's not always the most efficient. Another approach involves trying to find an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). Unfortunately, for 5/12, this is not easily achievable. The prime factorization of 12 is 2 x 2 x 3, and to obtain a power of 10, we need only factors of 2 and 5. Since 3 is a factor of 12, we cannot directly convert it to a power of 10 denominator. This method is often more suitable for fractions with denominators that have only 2 and 5 as prime factors.
Method 3: Using a Calculator
The simplest way to convert 5/12 to a decimal is using a calculator. Simply divide 5 by 12. Most calculators will display the result as 0.4166666... or a similar representation, clearly showing the repeating decimal nature of the result.
Understanding Repeating Decimals
The result of converting 5/12 to a decimal is a repeating decimal, also known as a recurring decimal. This means that the decimal representation has a sequence of digits that repeats infinitely. In this case, the digit 6 repeats indefinitely. Repeating decimals are often represented using a bar over the repeating sequence, as shown above (0.416̅).
Practical Applications of Decimal Conversion
Converting fractions to decimals is crucial in various practical applications:
- Financial calculations: Dealing with percentages, interest rates, and monetary values often requires converting fractions to decimals.
- Scientific measurements: Many scientific measurements are expressed as decimals.
- Engineering and design: Precise calculations in engineering and design often involve decimal representation.
- Data analysis: In statistical analysis and data representation, decimals are commonly used.
- Everyday calculations: Even simple tasks like calculating tips or splitting bills often involve decimal calculations.
Frequently Asked Questions (FAQ)
Q: Is there a way to express 5/12 as a terminating decimal?
A: No, 5/12 cannot be expressed as a terminating decimal. A fraction can only be expressed as a terminating decimal if its denominator has only 2 and 5 as prime factors. Since 12 has a prime factor of 3, 5/12 will always result in a repeating decimal.
Q: How do I round 5/12 to a certain number of decimal places?
A: To round 5/12 to a specific number of decimal places, you can use the long division method or a calculator. For example, rounding to three decimal places gives 0.417. Rounding to two decimal places gives 0.42. The rounding rules apply as usual; if the next digit is 5 or greater, round up; otherwise, round down.
Q: What are some other examples of fractions that result in repeating decimals?
A: Many fractions with denominators that are not factors of powers of 10 will result in repeating decimals. For example, 1/3 = 0.3̅, 2/7 = 0.285714̅, and 5/6 = 0.83̅.
Conclusion
Converting 5/12 to its decimal equivalent (0.416̅) involves understanding the principles of fractions and decimals, and applying methods like long division or using a calculator. The result is a repeating decimal, a common occurrence when the denominator of the fraction contains prime factors other than 2 and 5. This seemingly simple conversion showcases the importance of understanding fundamental mathematical concepts and their applications in various fields. Mastering this skill provides a strong foundation for tackling more complex mathematical problems and real-world applications. The process is straightforward but requires attention to detail, especially when dealing with repeating decimals and rounding. Through practice and understanding the underlying concepts, you'll confidently convert fractions to decimals and build a solid mathematical foundation.
Latest Posts
Latest Posts
-
Uniform Layered Haircut
Sep 19, 2025
-
Durham Cathedral Photos
Sep 19, 2025
-
Fraction Of 23
Sep 19, 2025
-
5x 10 Factorise
Sep 19, 2025
-
How Draw Landscape
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5/12 As Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.