70 Of 170
interactiveleap
Sep 19, 2025 · 5 min read
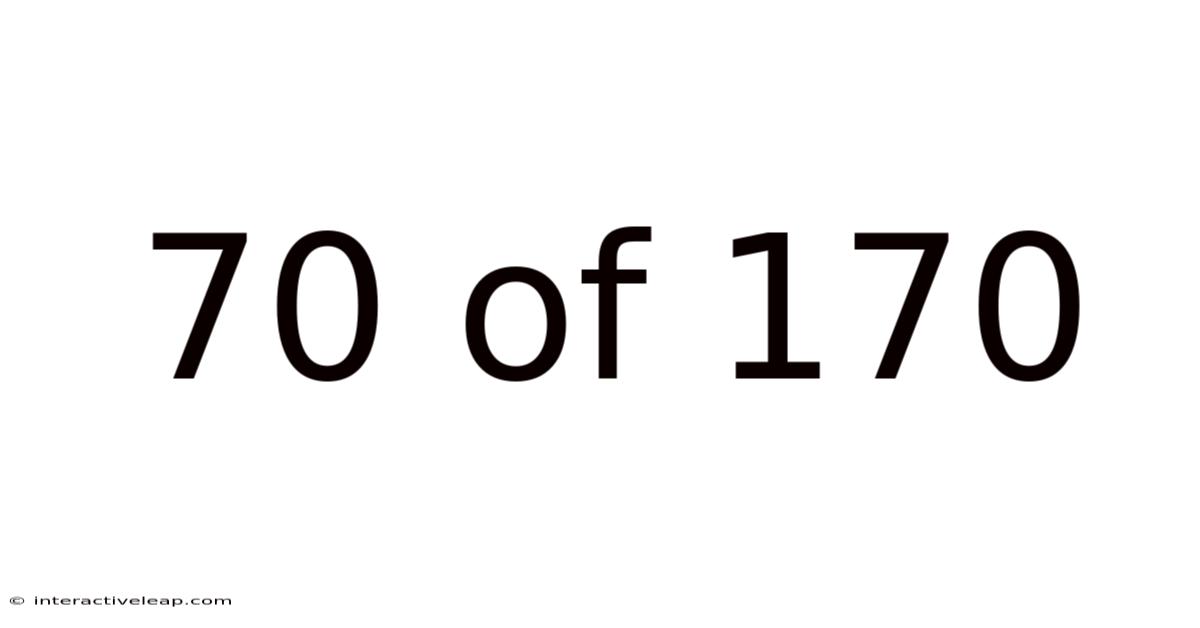
Table of Contents
Decoding the Enigma: Understanding the Fraction 70/170 and its Implications
The seemingly simple fraction 70/170 might appear insignificant at first glance. However, understanding this fraction and its various representations unlocks a deeper understanding of fundamental mathematical concepts, from simplification and ratio analysis to percentage calculations and their applications in real-world scenarios. This comprehensive guide will delve into the intricacies of 70/170, exploring its various forms, interpretations, and practical uses. We'll explore how to simplify this fraction, convert it to a decimal and percentage, and examine its significance in different contexts.
I. Simplifying the Fraction 70/170: Finding the Lowest Terms
The first step in working with any fraction is to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator (70) and the denominator (170) and dividing both by that number. Let's break down the process:
-
Finding the GCD: We can use the Euclidean algorithm or prime factorization to find the GCD of 70 and 170. Let's use prime factorization:
- 70 = 2 x 5 x 7
- 170 = 2 x 5 x 17
The common prime factors are 2 and 5. Therefore, the GCD is 2 x 5 = 10.
-
Simplifying the Fraction: Now, we divide both the numerator and the denominator by the GCD:
70 ÷ 10 = 7 170 ÷ 10 = 17
Therefore, the simplified fraction is 7/17. This is the most concise and mathematically accurate representation of the original fraction.
II. Converting 70/170 (or 7/17) to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case:
7 ÷ 17 ≈ 0.4117647
This decimal representation is an approximation because the division results in a non-terminating, repeating decimal. For practical purposes, we often round the decimal to a specific number of decimal places. Rounding to three decimal places, we get 0.412.
III. Converting 70/170 (or 7/17) to a Percentage
To convert a fraction to a percentage, we first convert it to a decimal (as shown above) and then multiply by 100%.
0.4117647 x 100% ≈ 41.17647%
Rounding to one decimal place, we get 41.2%. This means that 70/170 represents approximately 41.2% of a whole.
IV. Interpreting 70/170 in Real-World Contexts
The fraction 70/170, or its simplified form 7/17, can represent various real-world scenarios. Consider these examples:
- Test Scores: If a student answered 70 questions correctly out of a total of 170 questions on a test, their score would be 70/170, or 41.2%.
- Survey Results: If 70 out of 170 respondents to a survey answered "yes" to a particular question, then 41.2% of the respondents answered "yes".
- Production Efficiency: If a factory produced 70 units of a product out of a planned production of 170 units, their production efficiency would be 41.2%.
- Financial Ratios: The fraction could represent a financial ratio, such as the proportion of debt to equity in a company's balance sheet. Understanding such ratios is crucial for financial analysis.
V. Further Mathematical Explorations with 7/17
The simplified fraction 7/17 provides further opportunities for mathematical exploration:
- Finding Equivalent Fractions: Multiplying both the numerator and denominator of 7/17 by the same number will result in an equivalent fraction. For example, 14/34, 21/51, and 28/68 are all equivalent to 7/17.
- Reciprocal: The reciprocal of 7/17 is 17/7. Reciprocals are useful in various mathematical operations, including division.
- Decimal Expansion: As mentioned earlier, the decimal expansion of 7/17 is a non-terminating, repeating decimal. Analyzing the repeating pattern can be an exercise in number theory.
- Continued Fraction Representation: 7/17 can also be represented as a continued fraction, offering another perspective on its mathematical properties.
VI. Addressing Potential Misconceptions
It's crucial to address some common misconceptions related to fractions:
- The Importance of Simplification: While 70/170 and 7/17 are equivalent, 7/17 is preferred because it's simpler and easier to work with. Simplification reduces the risk of errors in calculations.
- Decimal Approximations: Remember that decimal representations of fractions are often approximations, especially for non-terminating decimals. The level of precision required depends on the context.
- Understanding Ratios: Fractions represent ratios. The ratio 7:17 indicates that for every 7 units of one quantity, there are 17 units of another quantity.
VII. Frequently Asked Questions (FAQs)
Q1: How do I know if a fraction is in its simplest form?
A1: A fraction is in its simplest form if the greatest common divisor (GCD) of its numerator and denominator is 1. In other words, there is no number (other than 1) that divides both the numerator and denominator evenly.
Q2: Why is simplifying fractions important?
A2: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also reduces the risk of errors and simplifies further mathematical operations.
Q3: Can I use a calculator to simplify fractions?
A3: Yes, many calculators have a function to simplify fractions. However, understanding the underlying principles of finding the GCD is essential for a deeper understanding of mathematics.
Q4: What if I need to add or subtract fractions that don't have the same denominator?
A4: You need to find a common denominator before adding or subtracting fractions. This involves finding the least common multiple (LCM) of the denominators.
Q5: Are there different methods for finding the GCD?
A5: Yes, the Euclidean algorithm and prime factorization are two common methods. The best method to use depends on the numbers involved.
VIII. Conclusion: The Broader Significance of 70/170
The seemingly simple fraction 70/170, once simplified to 7/17, opens a gateway to a deeper understanding of various mathematical concepts. From its simplification and conversion to decimals and percentages to its practical applications in diverse real-world scenarios, this fraction serves as a microcosm of the power and relevance of fractions in mathematics and beyond. By understanding its various representations and interpretations, we gain a stronger foundation in fundamental mathematical principles, enhancing our ability to solve problems and analyze data effectively in various fields. The exploration of 70/170 highlights the importance of not just calculating answers but also understanding the underlying concepts and their significance in practical contexts. This holistic approach to mathematical problem-solving is crucial for fostering a deeper and more meaningful understanding of the subject.
Latest Posts
Latest Posts
-
15 Off 24
Sep 19, 2025
-
15 Of 72
Sep 19, 2025
-
Grounded Split Screen
Sep 19, 2025
-
Is Hell Profanity
Sep 19, 2025
-
5 12 As Decimal
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 70 Of 170 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.