80 Of 16
interactiveleap
Sep 19, 2025 · 5 min read
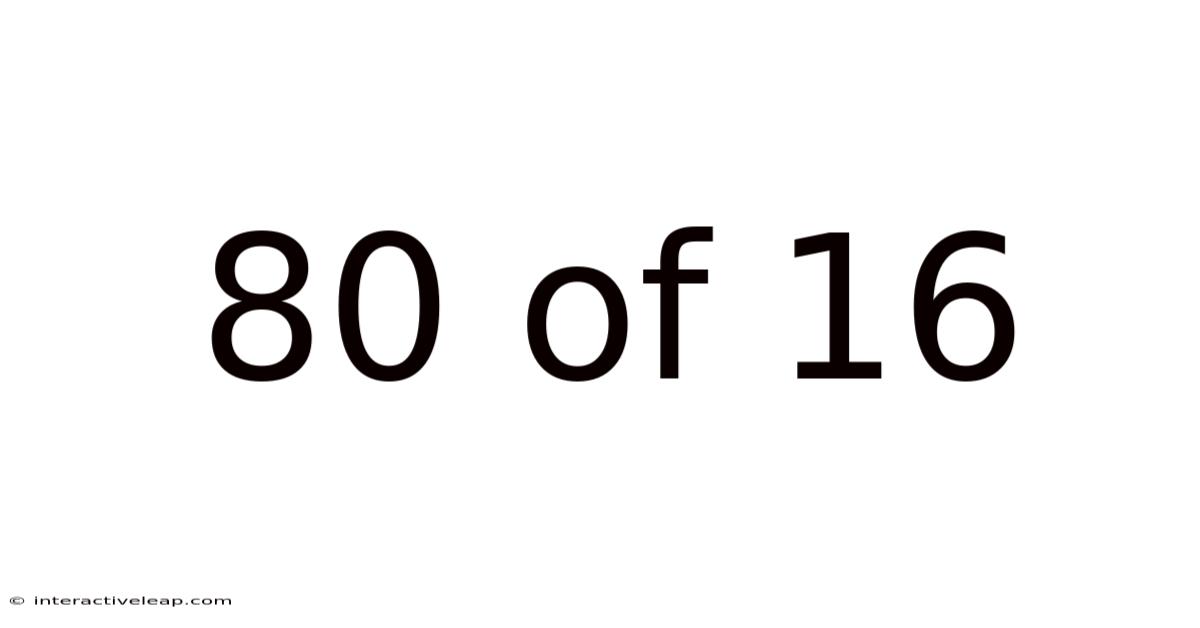
Table of Contents
Understanding 80/16: A Deep Dive into Fraction Simplification and its Applications
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in daily life and advanced studies. This article delves into the simplification of the fraction 80/16, exploring the process, underlying principles, and real-world examples. We'll cover the steps involved in simplifying fractions, explain the concept of greatest common divisor (GCD), and demonstrate how this simplification applies to different fields. By the end, you'll not only know the simplified form of 80/16 but also possess a stronger understanding of fraction manipulation.
Understanding Fractions: A Quick Recap
Before diving into 80/16, let's briefly review the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This represents three out of four equal parts.
Simplifying Fractions: The Core Concept
Simplifying a fraction means reducing it to its lowest terms. This is achieved by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Simplifying fractions doesn't change the value of the fraction; it just represents it in a more concise and manageable form.
Finding the GCD: Methods and Strategies
Several methods exist to find the GCD of two numbers. Let's explore a couple of common approaches:
-
Listing Factors: This method involves listing all the factors (numbers that divide evenly) of both the numerator and the denominator and identifying the largest factor they share. For example, the factors of 80 are 1, 2, 4, 5, 8, 10, 16, 20, 40, and 80. The factors of 16 are 1, 2, 4, 8, and 16. The largest common factor is 16.
-
Prime Factorization: This method involves breaking down both the numerator and the denominator into their prime factors (numbers divisible only by 1 and themselves). The GCD is then found by multiplying the common prime factors raised to their lowest power. Let's illustrate this with 80 and 16:
- 80 = 2 x 2 x 2 x 2 x 5 = 2⁴ x 5
- 16 = 2 x 2 x 2 x 2 = 2⁴
The common prime factor is 2, and the lowest power is 2⁴. Therefore, the GCD is 2⁴ = 16.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD. Let's apply it to 80 and 16:
- 80 ÷ 16 = 5 with a remainder of 0.
Since the remainder is 0, the GCD is the divisor, which is 16.
Simplifying 80/16: Step-by-Step Process
Now, let's apply the concepts learned to simplify the fraction 80/16. We've already determined that the GCD of 80 and 16 is 16. Therefore:
- Divide the numerator (80) by the GCD (16): 80 ÷ 16 = 5
- Divide the denominator (16) by the GCD (16): 16 ÷ 16 = 1
- The simplified fraction is: 5/1, which is equivalent to 5.
Therefore, 80/16 simplifies to 5.
Real-World Applications of Fraction Simplification
Simplifying fractions is not just an academic exercise; it has practical applications in various fields:
-
Cooking and Baking: Recipes often involve fractions. Simplifying fractions helps in accurately measuring ingredients. For example, if a recipe calls for 80/16 cups of flour, simplifying it to 5 cups makes the measurement much easier.
-
Construction and Engineering: In construction and engineering, precise measurements are essential. Simplifying fractions helps in calculations involving dimensions, material quantities, and proportions.
-
Finance and Accounting: Fractions are used extensively in financial calculations, such as calculating interest rates, profit margins, and ratios. Simplifying fractions makes these calculations clearer and easier to understand.
-
Data Analysis and Statistics: Fractions are used to represent proportions and probabilities in data analysis and statistics. Simplifying fractions makes it easier to interpret and present data.
Beyond 80/16: Extending the Concept
The principles involved in simplifying 80/16 apply to any fraction. The key is to find the GCD of the numerator and denominator and divide both by it. Let's consider some examples:
-
Simplifying 24/36: The GCD of 24 and 36 is 12. Therefore, 24/36 simplifies to 2/3.
-
Simplifying 105/15: The GCD of 105 and 15 is 15. Therefore, 105/15 simplifies to 7/1 or 7.
-
Simplifying 48/64: The GCD of 48 and 64 is 16. Therefore, 48/64 simplifies to 3/4.
Frequently Asked Questions (FAQ)
Q: What happens if the GCD is 1?
A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form. It cannot be simplified further. Such fractions are called irreducible fractions.
Q: Is there a shortcut to find the GCD?
A: For smaller numbers, listing factors can be quick. For larger numbers, the Euclidean Algorithm is generally more efficient. Prime factorization is also a reliable method, but it can be time-consuming for very large numbers.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It provides a more concise and manageable representation of the fraction's value.
Q: Can I simplify a fraction by dividing the numerator and denominator by any common factor?
A: While you can divide by any common factor, it's most efficient to divide by the greatest common factor (GCD) to obtain the simplest form in a single step. Dividing by smaller common factors may require multiple steps to reach the simplest form.
Conclusion: Mastering Fraction Simplification
Understanding fraction simplification is a crucial skill for success in mathematics and various other fields. The process involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. We've explored different methods for finding the GCD and applied them to simplify the fraction 80/16, which simplifies to 5. Mastering this skill will enhance your mathematical abilities and improve your problem-solving skills in various contexts. Remember, practice is key to mastering this fundamental mathematical concept! By understanding the underlying principles and practicing different methods, you'll confidently navigate the world of fractions.
Latest Posts
Latest Posts
-
Grounded Split Screen
Sep 19, 2025
-
Is Hell Profanity
Sep 19, 2025
-
5 12 As Decimal
Sep 19, 2025
-
60 Of 205
Sep 19, 2025
-
Farm En Espanol
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 80 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.