Factorise 12x 8
interactiveleap
Sep 18, 2025 · 6 min read
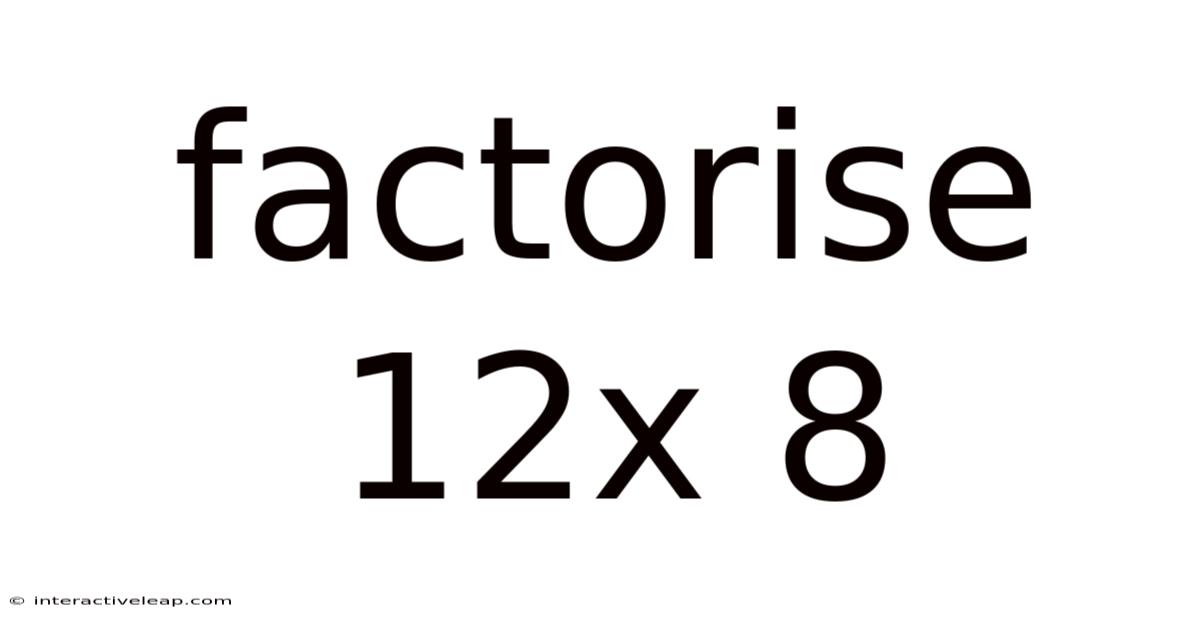
Table of Contents
Factorising 12x⁸: A Comprehensive Guide
This article provides a thorough exploration of factorising the algebraic expression 12x⁸. We'll move beyond a simple answer to delve into the underlying principles of factorization, covering various methods and exploring the reasons behind each step. This understanding is crucial for anyone studying algebra, from beginners grasping the basics to more advanced students tackling complex polynomial expressions. Understanding factorization is key to simplifying expressions, solving equations, and mastering higher-level mathematical concepts.
Introduction to Factorization
Factorization, in the context of algebra, involves breaking down a mathematical expression into simpler components – its factors – that when multiplied together, produce the original expression. Think of it like reverse multiplication. Just as 12 can be factored into 2 x 2 x 3, algebraic expressions can be broken down into simpler parts. This process is essential for simplifying complex expressions, solving equations, and understanding the structure of polynomials. Mastering factorization techniques is crucial for success in algebra and beyond.
Understanding the Components of 12x⁸
Before we begin factoring 12x⁸, let's understand its constituent parts:
-
12: This is the numerical coefficient. It's a constant number that multiplies the variable term. We can factorize 12 into its prime factors: 2 x 2 x 3 (or 2² x 3).
-
x⁸: This is the variable term. 'x' represents a variable, and the superscript '8' indicates the exponent, meaning 'x' is multiplied by itself eight times (x * x * x * x * x * x * x * x).
Therefore, 12x⁸ represents 12 multiplied by x multiplied by itself eight times.
Step-by-Step Factorization of 12x⁸
The factorization of 12x⁸ is relatively straightforward because it involves a numerical coefficient and a single variable term raised to a power. Here’s the process:
-
Factor the coefficient: Begin by finding the prime factorization of the numerical coefficient, 12. As mentioned earlier, 12 = 2 x 2 x 3 = 2² x 3.
-
Factor the variable term: Next, factor the variable term, x⁸. This involves expressing it as a product of its base (x) multiplied by itself the number of times indicated by the exponent (8). This can be written as x * x * x * x * x * x * x * x. Alternatively, and more concisely, we can express it as x⁸.
-
Combine the factors: Now, combine the prime factors of the coefficient and the factored variable term to get the complete factorization. This gives us: 2 x 2 x 3 x x x x x x x x x = 2² x 3 x x⁸
Therefore, the complete factorization of 12x⁸ is 2² x 3 x x⁸. This is the most complete factorization, expressing it as a product of prime numbers and the base variable. However, depending on the context, other forms might be acceptable. For instance, we could also write it as:
- 4 x 3 x x⁸ (combining the 2 x 2 as 4)
- 12x⁸ (although this is simply the original expression, not a factorization into simpler terms).
Further Exploration of Factorization Techniques
While the factorization of 12x⁸ is relatively simple, it serves as a foundation for understanding more complex factorization techniques. Let's briefly explore some of them:
-
Greatest Common Factor (GCF): This method involves identifying the largest common factor among the terms of an expression. For example, if we had the expression 12x⁸ + 6x⁴, the GCF would be 6x⁴. Factoring this out, we get 6x⁴(2x⁴ + 1).
-
Difference of Squares: This technique applies to expressions of the form a² - b², which factorizes to (a + b)(a - b). For instance, x² - 9 factors to (x + 3)(x - 3).
-
Trinomial Factoring: This method is used to factor expressions of the form ax² + bx + c. This often involves finding two numbers that add up to 'b' and multiply to 'ac'.
-
Grouping: This technique involves grouping terms within an expression to reveal common factors. It's particularly useful for expressions with four or more terms.
-
Factoring by Completing the Square: This method involves manipulating a quadratic expression to create a perfect square trinomial, allowing for easier factorization.
-
Cubic and Higher-Order Polynomials: Factoring cubic and higher-order polynomials can be more challenging and often involves techniques like synthetic division or the rational root theorem.
Illustrative Examples
Let’s look at a few more examples to further solidify our understanding:
Example 1: Factorize 20x⁵
The prime factorization of 20 is 2² x 5. Therefore, the factorization is 2² x 5 x x⁵.
Example 2: Factorize 36x¹²y⁶
The prime factorization of 36 is 2² x 3². Thus, the factorization is 2² x 3² x x¹² x y⁶.
Example 3: Factorize 24x³ + 12x²
Here, we can use the GCF method. The GCF of 24x³ and 12x² is 12x². Factoring this out, we obtain 12x²(2x + 1).
Frequently Asked Questions (FAQ)
Q1: What are prime factors?
A1: Prime factors are prime numbers that multiply together to give the original number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
Q2: Why is factorization important?
A2: Factorization simplifies complex expressions, making them easier to manipulate and understand. It's fundamental to solving equations, simplifying fractions, and performing other algebraic operations.
Q3: Can I factorize every algebraic expression?
A3: Not every algebraic expression can be easily factored. Some expressions might be irreducible, meaning they cannot be factored into simpler terms using standard techniques.
Q4: What if I have a negative coefficient?
A4: If the coefficient is negative, factor out the negative sign along with the other factors. For example, -12x⁸ would factor to -1 x 2² x 3 x x⁸.
Q5: Are there different ways to write the factorization?
A5: Yes, there can be slightly different ways to write the factorization depending on whether you choose to combine factors or leave them as prime factors. The important thing is that when you multiply all the factors back together, you get the original expression.
Conclusion
Factorizing algebraic expressions, even seemingly simple ones like 12x⁸, is a foundational skill in algebra. Understanding the underlying principles – breaking down the numerical coefficient into its prime factors and expressing the variable term as a product of its base – provides the groundwork for mastering more complex factorization techniques. The ability to efficiently factorize expressions is crucial for progressing in higher-level mathematics. Through practice and application, you can develop confidence and proficiency in this essential algebraic skill. Remember to always check your work by multiplying your factors together to ensure they produce the original expression. The more you practice, the faster and more efficient you’ll become at factorization.
Latest Posts
Latest Posts
-
42 In Binary
Sep 18, 2025
-
4x5 In Pixels
Sep 18, 2025
-
25 Of 8
Sep 18, 2025
-
75 Of 36
Sep 18, 2025
-
3000g To Lbs
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about Factorise 12x 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.