75 Of 36
interactiveleap
Sep 18, 2025 · 6 min read
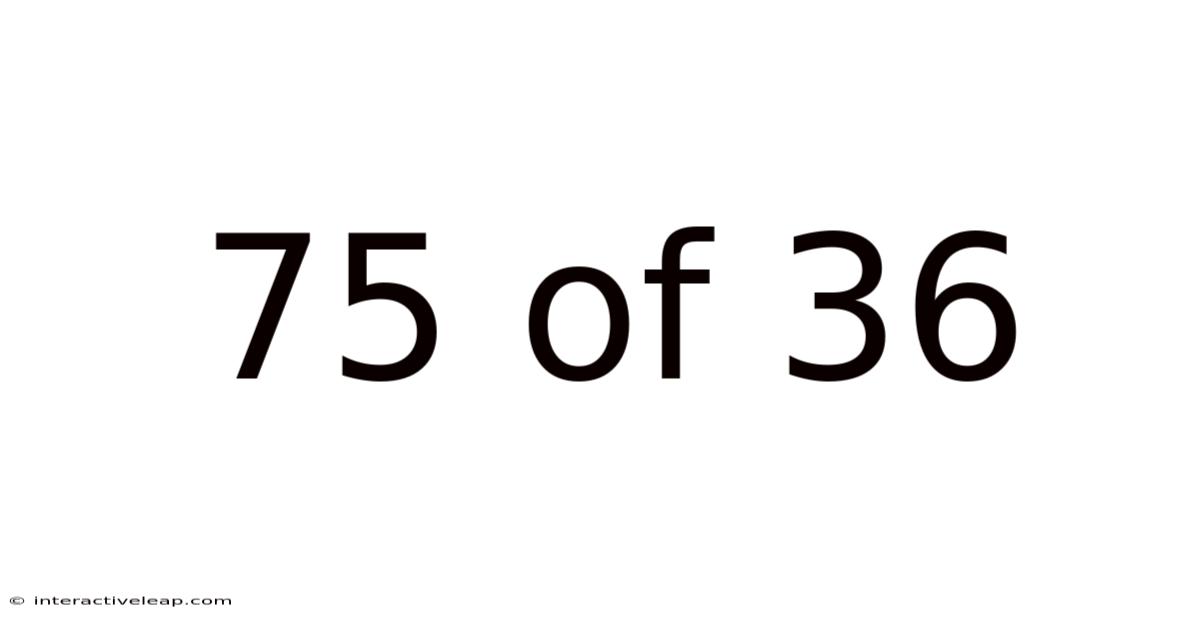
Table of Contents
Decoding the Fraction: Understanding 75/36 and its Implications
The seemingly simple fraction 75/36 might appear straightforward at first glance. However, a deeper dive reveals a wealth of mathematical concepts and practical applications. This article will explore 75/36 in detail, covering its simplification, decimal representation, percentage equivalent, real-world applications, and related mathematical principles. Understanding fractions like this is fundamental to mastering arithmetic, algebra, and even more advanced mathematical fields.
Introduction: What is 75/36?
75/36 represents a fraction, a part of a whole. It indicates that we have 75 parts out of a total of 36 parts. Immediately, we can see that this is an improper fraction, meaning the numerator (75) is larger than the denominator (36). This implies that the fraction represents a value greater than one. Understanding improper fractions is crucial for various mathematical operations and real-world problem-solving. This article will guide you through simplifying this fraction, converting it to a decimal and percentage, and exploring its significance in different contexts.
Simplifying 75/36: Finding the Greatest Common Divisor (GCD)
Before we proceed with further calculations, it's essential to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (75) and the denominator (36). The GCD is the largest number that divides both 75 and 36 without leaving a remainder.
One method to find the GCD is through prime factorization. Let's break down both numbers:
- 75: 3 x 5 x 5 (or 3 x 5²)
- 36: 2 x 2 x 3 x 3 (or 2² x 3²)
The common prime factors are 3. Therefore, the GCD of 75 and 36 is 3.
Now, we divide both the numerator and the denominator by the GCD:
75 ÷ 3 = 25 36 ÷ 3 = 12
Therefore, the simplified form of 75/36 is 25/12. This simplified fraction is still an improper fraction, representing a value greater than one.
Converting 25/12 to a Decimal: Long Division
To express 25/12 as a decimal, we perform long division. We divide the numerator (25) by the denominator (12):
2.08333...
12 | 25.00000
24
10
0
100
96
40
36
40
36
4...
The division results in a repeating decimal: 2.08333... The '3' repeats infinitely. This can be written as 2.083̅. Understanding repeating decimals is crucial in various mathematical and scientific applications.
Converting 25/12 to a Percentage:
To convert the fraction 25/12 to a percentage, we first convert it to a decimal (as shown above: 2.08333...) and then multiply by 100:
2.08333... x 100 = 208.333...% or approximately 208.33%. This percentage indicates that 25/12 represents 208.33% of a whole.
Real-World Applications of 75/36 (and 25/12):
Fractions like 75/36, and its simplified form 25/12, find applications in numerous real-world scenarios:
-
Measurement and Proportion: Imagine you're measuring a length of fabric. If you need 75 centimeters and you only have 36 centimeters per piece, you would need more than one piece (more specifically, 25/12 pieces which is roughly 2.08 pieces).
-
Resource Allocation: Suppose you have 75 resources (e.g., workers, materials) to allocate among 36 tasks. The fraction 75/36 tells you that on average, you can allocate more than two resources per task.
-
Recipe Scaling: Consider a recipe that calls for 36 grams of flour but you want to make a larger batch using 75 grams of flour. The ratio 75/36 (or 25/12) would help you proportionally increase the quantities of other ingredients.
-
Financial Calculations: Fractions are frequently used in financial calculations, such as determining proportions of investments or calculating interest rates. Understanding fractions is fundamental for making informed financial decisions.
-
Engineering and Construction: In engineering and construction, fractions are essential for precise measurements and calculations related to dimensions, materials, and structural designs.
Mathematical Concepts Related to 75/36:
Understanding 75/36 involves several key mathematical concepts:
-
Improper Fractions: As mentioned, 75/36 is an improper fraction because the numerator is greater than the denominator. Improper fractions often represent quantities exceeding one whole.
-
Mixed Numbers: An improper fraction can be converted to a mixed number, which combines a whole number and a proper fraction. For 25/12, we can perform the division to obtain: 25 ÷ 12 = 2 with a remainder of 1. This is written as 2 1/12.
-
Decimal Representation: Converting fractions to decimals involves long division. The result can be a terminating decimal (with a finite number of digits after the decimal point) or a repeating decimal (with an infinitely repeating sequence of digits).
-
Percentage Conversion: Expressing a fraction as a percentage allows for easy comparison and interpretation in relative terms.
-
Ratio and Proportion: Fractions represent ratios, which compare the relative sizes of two quantities. Understanding ratios is essential for solving problems involving proportions.
-
Greatest Common Divisor (GCD): Finding the GCD allows for simplification of fractions to their lowest terms, making calculations easier and results clearer.
-
Least Common Multiple (LCM): While not directly used in the simplification of 75/36, the LCM is crucial when adding or subtracting fractions with different denominators.
Frequently Asked Questions (FAQ):
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes calculations easier and presents results in a more concise and understandable manner. It also helps in identifying patterns and relationships between numbers.
-
Q: How do I convert a fraction to a percentage?
- A: First, convert the fraction to a decimal by dividing the numerator by the denominator. Then, multiply the decimal by 100 and add a "%" sign.
-
Q: What is a mixed number?
- A: A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator). It's an alternative way to represent an improper fraction.
-
Q: What if the decimal representation of a fraction is non-terminating and non-repeating?
- A: This implies the fraction represents an irrational number, which cannot be expressed as a simple fraction. Examples include π (pi) and √2 (the square root of 2).
-
Q: Can I use a calculator to simplify fractions?
- A: Yes, many calculators have functions for simplifying fractions and performing other fraction-related calculations.
Conclusion:
The seemingly simple fraction 75/36, when explored thoroughly, reveals a rich tapestry of mathematical concepts and real-world applications. Simplifying it to 25/12, converting it to its decimal (2.083̅) and percentage (208.33%) equivalents, and understanding its implications in various contexts highlights the importance of mastering fractions. This fundamental skill forms the bedrock of more advanced mathematical understanding and practical problem-solving across diverse fields. From measuring ingredients in a recipe to allocating resources in a project, a deep understanding of fractions like 75/36 is invaluable. By understanding the underlying principles, you equip yourself with a powerful tool for tackling numerical challenges in daily life and beyond.
Latest Posts
Latest Posts
-
0 4as A Fraction
Sep 18, 2025
-
Infusion Rate Formula
Sep 18, 2025
-
Millicents Prosthesis Location
Sep 18, 2025
-
30 Of 16
Sep 18, 2025
-
51 1kg To Lbs
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.