25 Of 8
interactiveleap
Sep 18, 2025 · 6 min read
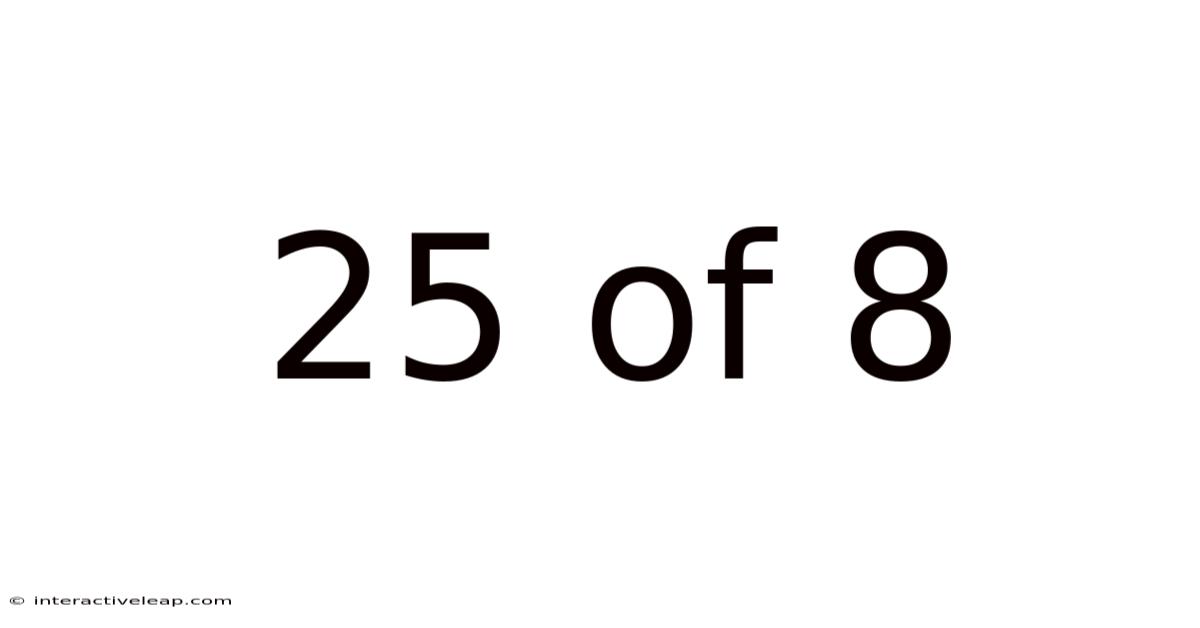
Table of Contents
Decoding the Enigma: Understanding 25/8 and its Applications
The fraction 25/8, seemingly simple at first glance, unlocks a world of mathematical concepts and practical applications. This article delves deep into the meaning, calculation, conversion, and various uses of this fraction, catering to readers from diverse mathematical backgrounds – from beginners grappling with basic fractions to those exploring more advanced applications. We'll explore its decimal representation, percentage equivalent, applications in measurement and problem-solving, and even touch upon its significance in certain fields.
Introduction: What is 25/8?
25/8 is a fraction representing the ratio of 25 parts to 8 parts. It's an improper fraction because the numerator (25) is larger than the denominator (8). This signifies a value greater than 1. Understanding improper fractions is crucial for various mathematical operations and real-world applications. This seemingly straightforward fraction can be used to illustrate numerous mathematical principles and has practical uses across different disciplines. We'll explore these aspects in detail throughout this article.
1. Converting 25/8 to its Decimal Equivalent:
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case:
25 ÷ 8 = 3.125
Therefore, 25/8 is equal to 3.125. This decimal representation is often easier to use in calculations and comparisons, especially when dealing with units of measurement or scientific data.
2. Expressing 25/8 as a Percentage:
To express 25/8 as a percentage, we first convert it to a decimal (as shown above) and then multiply by 100%:
3.125 × 100% = 312.5%
Thus, 25/8 is equivalent to 312.5%. Percentage representation is valuable when comparing proportions or illustrating changes in quantities.
3. Converting 25/8 to a Mixed Number:
An improper fraction like 25/8 can also be expressed as a mixed number. This involves dividing the numerator (25) by the denominator (8) and expressing the result as a whole number and a remaining fraction:
25 ÷ 8 = 3 with a remainder of 1
This can be written as 3 1/8. Therefore, 25/8 is equal to 3 1/8. Mixed numbers are helpful when visualizing quantities or performing certain calculations.
4. Applications of 25/8 in Measurement:
The fraction 25/8 finds practical applications in various measurement scenarios. Consider these examples:
-
Length: If you have a piece of material 25/8 meters long, you can easily convert it to its decimal equivalent (3.125 meters) or mixed number equivalent (3 1/8 meters) for easier understanding and use.
-
Weight: If a package weighs 25/8 kilograms, understanding its decimal (3.125 kg) or mixed number (3 1/8 kg) representation is crucial for shipping calculations, etc.
-
Volume: Suppose a container holds 25/8 liters of liquid. The decimal and mixed number conversions facilitate accurate calculations involving the liquid's volume.
5. Solving Problems Using 25/8:
Let's consider a few problem-solving scenarios involving 25/8:
-
Scenario 1: Sharing Equally: If you have 25 cookies and want to share them equally among 8 friends, each friend receives 25/8 cookies. Converting this to a mixed number (3 1/8) helps visualize that each friend gets 3 whole cookies, and there's 1 cookie left to be divided among the 8 friends (1/8 of a cookie each).
-
Scenario 2: Calculating Costs: If the cost of 8 items is $25, the cost of one item is $25/8. Converting this to a decimal ($3.125) is helpful for calculating the total cost of a larger quantity.
-
Scenario 3: Unit Conversions: Imagine you need to convert 25/8 inches to centimeters. You first convert the fraction to its decimal equivalent (3.125 inches), then use the conversion factor (1 inch ≈ 2.54 cm) to find the result in centimeters.
6. Advanced Applications: Engineering and Scientific Fields
While seemingly simple, the fraction 25/8, or its decimal equivalent 3.125, pops up in more sophisticated contexts:
-
Engineering Design: In engineering drawings and designs, precise measurements are critical. The fraction, and its decimal form, could represent a crucial dimension of a component or structure. Accuracy is paramount, hence the importance of mastering fraction manipulation.
-
Computer Science: In computer programming and data representation, binary and fractional numbers are fundamental. The decimal 3.125 has a specific binary representation that's important for computer processing and storage.
-
Financial Calculations: In interest calculations or other financial computations, the precise value of 3.125 might be crucial for accurate results. Slight variations in calculations, especially those involving large sums, can have significant consequences.
7. Understanding the Underlying Mathematical Concepts:
Working with 25/8 provides opportunities to reinforce understanding of key mathematical concepts:
-
Fraction Arithmetic: Adding, subtracting, multiplying, and dividing fractions are essential skills. 25/8 provides excellent practice material for honing these skills.
-
Decimal Representation: Converting fractions to decimals is a crucial step in many calculations. The conversion of 25/8 to 3.125 helps in understanding this process.
-
Percentage Calculations: Expressing fractions as percentages is vital for comparisons and understanding proportions. The conversion of 25/8 to 312.5% demonstrates this concept effectively.
-
Mixed Numbers: Converting improper fractions to mixed numbers enhances comprehension and visualization of quantities. Representing 25/8 as 3 1/8 showcases this effectively.
8. Frequently Asked Questions (FAQ):
-
Q: Is 25/8 a rational number? A: Yes, 25/8 is a rational number because it can be expressed as a ratio of two integers.
-
Q: How do I simplify 25/8? A: 25/8 is already in its simplest form because 25 and 8 do not share any common factors other than 1.
-
Q: Can 25/8 be expressed as a terminating decimal? A: Yes, 25/8 results in a terminating decimal (3.125) because its denominator (8) has only 2 and 5 as prime factors.
-
Q: What are some real-world examples where I might encounter 25/8? A: You might encounter it in measurements of length, weight, volume, or in problem-solving scenarios involving sharing or cost calculations. It also has applications in various engineering and scientific fields, although this would often be represented in decimal form.
9. Conclusion: The Significance of Understanding 25/8
While seemingly a simple fraction, 25/8 serves as a powerful tool for illustrating fundamental mathematical concepts and for solving various practical problems. Understanding its decimal and percentage equivalents, along with its representation as a mixed number, broadens our mathematical understanding and enhances our ability to solve real-world problems across multiple disciplines. Mastering the manipulation of fractions like 25/8 is not merely an academic exercise; it’s a crucial skill that translates directly into practical applications and more advanced mathematical studies. The seemingly simple act of understanding this fraction opens doors to a deeper understanding of the broader world of mathematics and its vast applications. Continue practicing your fraction skills, and you'll find your understanding of mathematics expanding exponentially. The journey of mathematical understanding is a rewarding one, and seemingly simple fractions like 25/8 can serve as excellent stepping stones along the way.
Latest Posts
Latest Posts
-
Bottomless Bucket Terraria
Sep 18, 2025
-
0 4as A Fraction
Sep 18, 2025
-
Infusion Rate Formula
Sep 18, 2025
-
Millicents Prosthesis Location
Sep 18, 2025
-
30 Of 16
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.