42 In Binary
interactiveleap
Sep 18, 2025 · 6 min read
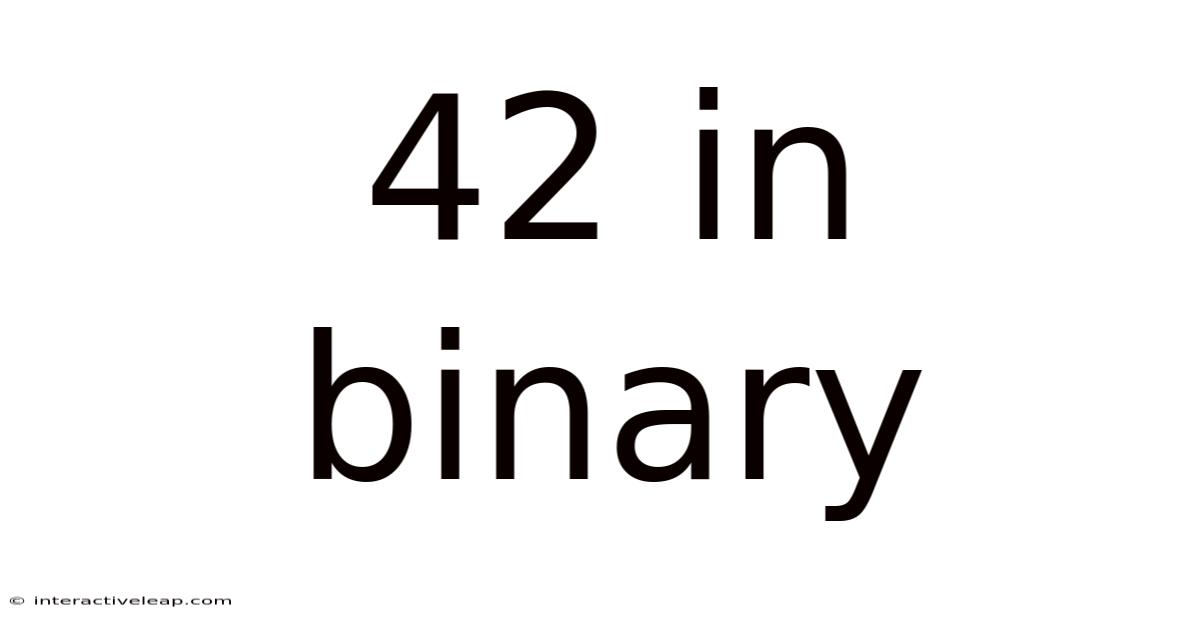
Table of Contents
Decoding 42: A Deep Dive into Binary Representation
The number 42. For fans of The Hitchhiker's Guide to the Galaxy, it's the answer to the ultimate question of life, the universe, and everything. But for computer scientists and anyone interested in the fundamental workings of digital systems, 42 holds a different, equally fascinating significance: its binary representation. This article will explore the concept of binary, explain how to convert decimal numbers like 42 into binary, delve into the underlying mathematics, and address common questions surrounding binary representation. We'll also touch upon the practical applications of binary in computing and beyond.
Understanding the Binary System
Before diving into the specifics of 42 in binary, let's establish a clear understanding of the binary number system itself. Unlike the decimal system (base-10), which uses ten digits (0-9), the binary system (base-2) uses only two digits: 0 and 1. This seemingly simple difference is fundamental to how computers and digital devices operate. These 0s and 1s represent the two states of a transistor – either on (1) or off (0) – forming the building blocks of all digital information.
Each position in a binary number represents a power of 2, starting from 2<sup>0</sup> (the rightmost position) and increasing towards the left. For example:
- 2<sup>0</sup> = 1
- 2<sup>1</sup> = 2
- 2<sup>2</sup> = 4
- 2<sup>3</sup> = 8
- 2<sup>4</sup> = 16
- 2<sup>5</sup> = 32
- 2<sup>6</sup> = 64
- and so on...
Converting Decimal to Binary: The Method
Now, let's convert the decimal number 42 into its binary equivalent. We can use a few different methods, but the most straightforward involves successive division by 2.
Method 1: Successive Division by 2
- Divide: Divide 42 by 2. The result is 21 with a remainder of 0.
- Record Remainder: Note down the remainder (0).
- Repeat: Divide the quotient (21) by 2. The result is 10 with a remainder of 1.
- Record Remainder: Note down the remainder (1).
- Continue: Continue this process until the quotient becomes 0.
Here's the complete process:
| Division | Quotient | Remainder |
|---|---|---|
| 42 / 2 | 21 | 0 |
| 21 / 2 | 10 | 1 |
| 10 / 2 | 5 | 0 |
| 5 / 2 | 2 | 1 |
| 2 / 2 | 1 | 0 |
| 1 / 2 | 0 | 1 |
- Read Remainders in Reverse: Read the remainders from bottom to top. This sequence represents the binary equivalent of 42.
Therefore, 42 in decimal is 101010 in binary.
Method 2: Subtracting Powers of 2
This method involves subtracting the largest possible power of 2 from the decimal number and repeating the process until you reach 0.
- Find Largest Power: Identify the largest power of 2 that is less than or equal to 42. This is 32 (2<sup>5</sup>).
- Subtract: Subtract 32 from 42, leaving 10.
- Repeat: Repeat step 1 and 2 with the remaining value (10). The largest power of 2 less than or equal to 10 is 8 (2<sup>3</sup>). Subtracting 8 from 10 leaves 2.
- Continue: Continue this process until you reach 0.
Here's the breakdown:
- 42 - 32 = 10
- 10 - 8 = 2
- 2 - 2 = 0
- Represent as Binary: Each subtracted power of 2 represents a '1' in the binary representation, while any unused powers of 2 represent a '0'. Since we subtracted 32 (2<sup>5</sup>), 8 (2<sup>3</sup>), and 2 (2<sup>1</sup>), our binary representation is 101010.
Verification and Understanding the Result
We've shown two different methods to arrive at the binary representation of 42 as 101010. Let's verify this result by converting it back to decimal:
(1 x 2<sup>5</sup>) + (0 x 2<sup>4</sup>) + (1 x 2<sup>3</sup>) + (0 x 2<sup>2</sup>) + (1 x 2<sup>1</sup>) + (0 x 2<sup>0</sup>) = 32 + 0 + 8 + 0 + 2 + 0 = 42
This confirms that 101010 is indeed the correct binary representation of 42.
Binary in Computing: Practical Applications
The binary system is the foundation of modern computing. Every piece of data – text, images, videos, programs – is ultimately represented as a sequence of 0s and 1s within a computer's memory and processing units. This is because the binary system provides a simple and efficient way to represent and manipulate information using electronic circuits.
Here are some key applications:
- Data Storage: Hard drives, SSDs, and other storage devices store data as magnetized or charged states, representing 0s and 1s.
- Memory: RAM (Random Access Memory) uses transistors to store data in binary format, allowing for rapid access and manipulation.
- Processor Operations: Central Processing Units (CPUs) perform arithmetic and logical operations on binary data, executing instructions encoded in binary code.
- Network Communication: Data transmitted over networks is encoded in binary format, facilitating communication between devices.
- Digital Signal Processing: Binary representation is crucial for processing digital signals in audio, video, and other applications.
Beyond 42: Exploring Larger Numbers and Other Bases
While we focused on 42, the methods described above apply to any decimal number. Converting larger numbers to binary simply involves extending the successive division or subtraction process. Furthermore, while binary is the fundamental system for computers, other number systems, such as hexadecimal (base-16) and octal (base-8), are often used as more concise representations of binary data for human readability.
Frequently Asked Questions (FAQ)
Q: Why is binary so important for computers?
A: Computers use transistors that can be either on or off, perfectly representing the two states of binary (0 and 1). This allows for simple and reliable manipulation of information using electronic circuits.
Q: Can I convert any decimal number to binary?
A: Yes, any decimal number can be converted to binary using the methods described above (successive division or subtraction of powers of 2).
Q: What about negative numbers in binary?
A: Negative numbers in binary are typically represented using techniques like two's complement, which involves inverting the bits and adding 1.
Q: Are there other number systems besides decimal and binary?
A: Yes, many other number systems exist, including hexadecimal (base-16), octal (base-8), ternary (base-3), and others. Each has its own unique properties and applications.
Conclusion: The Enduring Significance of Binary
The seemingly simple number 42, when viewed through the lens of binary, reveals the profound elegance and efficiency of this fundamental system. Understanding binary is not just about converting numbers; it’s about grasping the foundational language of computers and the digital world around us. From the smallest microcontrollers to the most powerful supercomputers, the ubiquitous presence of 0s and 1s underscores the enduring significance of the binary system in shaping our technologically advanced world. The next time you encounter the number 42, remember not just its literary significance, but also its crucial role in the digital realm, quietly orchestrating the seamless functioning of the technologies we rely on daily. Hopefully, this deep dive into the binary representation of 42 has broadened your understanding of this essential concept and sparked your interest in the fascinating world of computer science.
Latest Posts
Latest Posts
-
Sentence Using Aloud
Sep 18, 2025
-
Bottomless Bucket Terraria
Sep 18, 2025
-
0 4as A Fraction
Sep 18, 2025
-
Infusion Rate Formula
Sep 18, 2025
-
Millicents Prosthesis Location
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 42 In Binary . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.