80 X 2
interactiveleap
Sep 18, 2025 · 6 min read
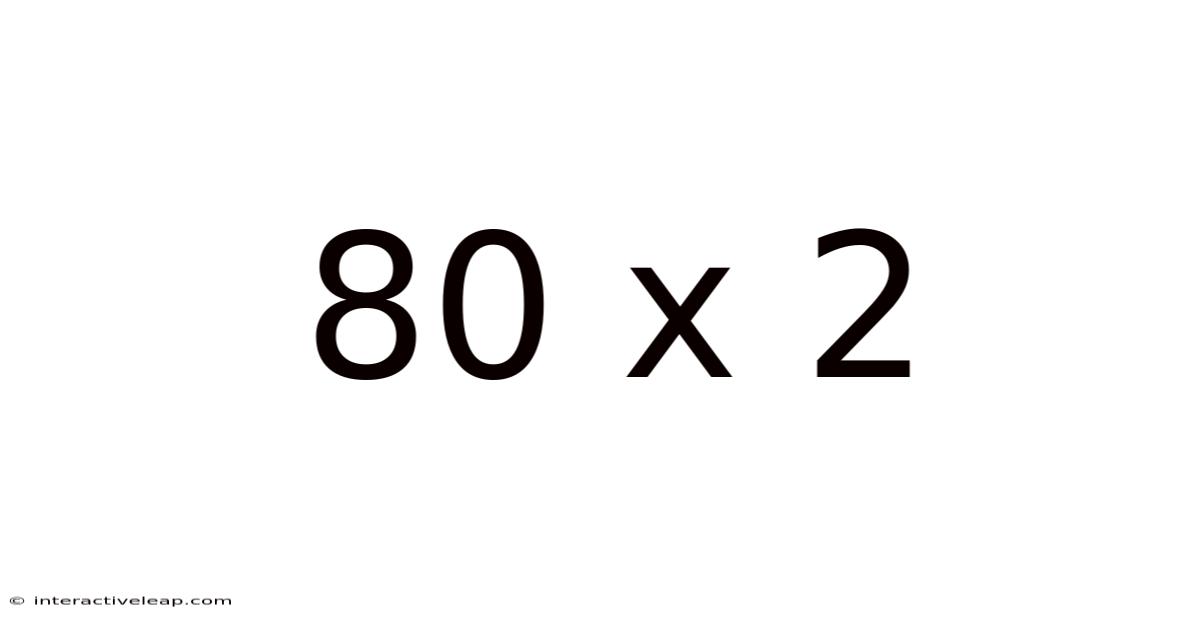
Table of Contents
Decoding 80 x 2: Exploring the Multiplicative Power of Simplicity
The seemingly simple equation, 80 x 2, holds far more depth than its initial appearance suggests. This seemingly elementary multiplication problem acts as a gateway to explore various mathematical concepts, practical applications, and even philosophical implications about the power of scaling and doubling. This article will delve into the intricacies of 80 x 2, examining its straightforward solution, exploring its applications across diverse fields, and addressing common misconceptions. We'll uncover the beauty of simple mathematics and its surprising power to shape our understanding of the world.
Understanding the Fundamentals: Solving 80 x 2
At its core, 80 x 2 represents a multiplication problem. Multiplication is essentially repeated addition. Therefore, 80 x 2 can be understood as adding 80 to itself once: 80 + 80 = 160. Alternatively, we can utilize the properties of multiplication to simplify the calculation. We can break down 80 into its constituent parts (8 x 10) and then multiply: (8 x 10) x 2 = 160. This demonstrates the flexibility and efficiency of mathematical operations. The answer, unequivocally, is 160.
Practical Applications: Where 80 x 2 Makes a Difference
The seemingly simple act of multiplying 80 by 2 finds widespread application across numerous domains. Let's explore some examples:
1. Business and Finance: Scaling Operations
Imagine a small business selling handmade crafts. If they currently sell 80 units per month and aim to double their sales, they would need to reach 160 units. This seemingly small calculation informs crucial business decisions like production planning, inventory management, and marketing strategies. Understanding the impact of doubling sales allows for realistic projections and informed resource allocation.
2. Engineering and Design: Doubling Capacity
In engineering, scaling up designs often involves straightforward multiplication. For instance, if a structural component can support a load of 80 tons, doubling its size (within the constraints of material properties) might increase its load capacity to 160 tons. This principle underpins numerous design considerations in infrastructure projects, aerospace engineering, and industrial manufacturing.
3. Data Analysis and Statistics: Understanding Growth Rates
Consider a scenario where a website has 80,000 unique visitors per day. If the website’s popularity doubles, it would attract 160,000 unique visitors. This doubling represents a significant growth rate and has considerable implications for server capacity, website performance, and advertising revenue projections.
4. Everyday Life: Doubling Recipes and Quantities
Even in everyday life, the principle of doubling is frequently used. If a recipe calls for 80 grams of flour, doubling the recipe would require 160 grams. Similarly, this principle applies to various household tasks and activities where scaling up quantities is necessary.
Exploring the Concept of Doubling: Exponential Growth
The act of multiplying by two is intrinsically linked to the concept of exponential growth. Exponential growth represents a phenomenon where a quantity increases at a rate proportional to its current value. This rapid increase can be observed in various natural processes like bacterial growth, compound interest calculations, and the spread of viral information online.
Understanding exponential growth requires recognizing the power of compounding. Each doubling represents a significant increase, and repeated doublings lead to a dramatic expansion. In the case of 80 x 2, this initial doubling serves as the foundational step in understanding the potential for explosive growth when similar calculations are repeated over time.
Beyond the Numbers: The Significance of Simplicity
While the calculation 80 x 2 is straightforward, its simplicity should not be underestimated. This fundamental calculation emphasizes the importance of building strong foundational knowledge in mathematics. Mastering basic arithmetic is crucial for building a solid understanding of more complex mathematical concepts. The elegance of this simple equation highlights the beauty and power of mathematics as a tool for understanding and shaping our world.
Addressing Common Misconceptions: Avoiding Pitfalls in Multiplication
While multiplying 80 by 2 is relatively straightforward, some common misconceptions can lead to errors, especially when working with larger numbers or more complex calculations. Let's address some potential pitfalls:
-
Incorrect place value: When dealing with larger numbers, paying close attention to place value is critical. For instance, multiplying 800 by 2 requires careful consideration of the zero's place value, leading to the correct answer of 1600, not 160.
-
Misinterpreting multiplication as addition: While multiplication can be understood as repeated addition, it is essential to understand the distinct nature of both operations. Confusing the two can lead to incorrect results. For example, 80 + 2 ≠ 80 x 2.
-
Ignoring units: In real-world applications, it’s crucial to be mindful of the units involved. If 80 represents 80 kilograms, then 80 x 2 equals 160 kilograms, not just 160.
Frequently Asked Questions (FAQ)
Q1: What are some alternative ways to solve 80 x 2?
A1: Besides direct addition (80 + 80) and the standard multiplication method, you can also use distributive property. For example, you can break down 80 into 40 + 40, then multiply each by 2, and add the results: (40 x 2) + (40 x 2) = 80 + 80 = 160. You could also use a calculator for quick computation.
Q2: How does 80 x 2 relate to other mathematical concepts?
A2: 80 x 2 is directly related to concepts like exponential growth, scaling, proportions, and the distributive property. It forms the foundation for understanding more complex mathematical operations and problem-solving scenarios.
Q3: What are the real-world implications of understanding 80 x 2?
A3: Understanding this seemingly simple equation has far-reaching implications across diverse fields, including business planning, engineering design, data analysis, and everyday tasks. It highlights the importance of basic arithmetic and its application in problem-solving.
Q4: What if I need to multiply 80 by a number other than 2?
A4: The same fundamental principles apply. You would use the standard multiplication method or break down the numbers to simplify the calculation. The ability to perform 80 x 2 efficiently lays the groundwork for handling other multiplication problems effectively.
Conclusion: The Enduring Power of a Simple Equation
The equation 80 x 2, while seemingly simple, reveals a surprising depth of mathematical understanding and practical applications. From understanding exponential growth to applying it to real-world problems in various fields, the ability to solve this equation effectively highlights the importance of fundamental mathematical skills. The simplicity of 80 x 2 should not be underestimated; it serves as a powerful reminder of the enduring power and beauty inherent in even the most basic mathematical concepts. By grasping its implications, we can unlock a deeper appreciation for the role of mathematics in shaping our understanding of the world around us. The seemingly small step of solving 80 x 2 opens doors to a vast landscape of mathematical exploration and real-world applications, reinforcing the importance of strong foundational mathematical skills.
Latest Posts
Latest Posts
-
65 Of 180
Sep 18, 2025
-
60 Of 230
Sep 18, 2025
-
174lb In Kg
Sep 18, 2025
-
20 Of 40000
Sep 18, 2025
-
Does Anyone Know
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 80 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.