20 Of 40000
interactiveleap
Sep 18, 2025 · 5 min read
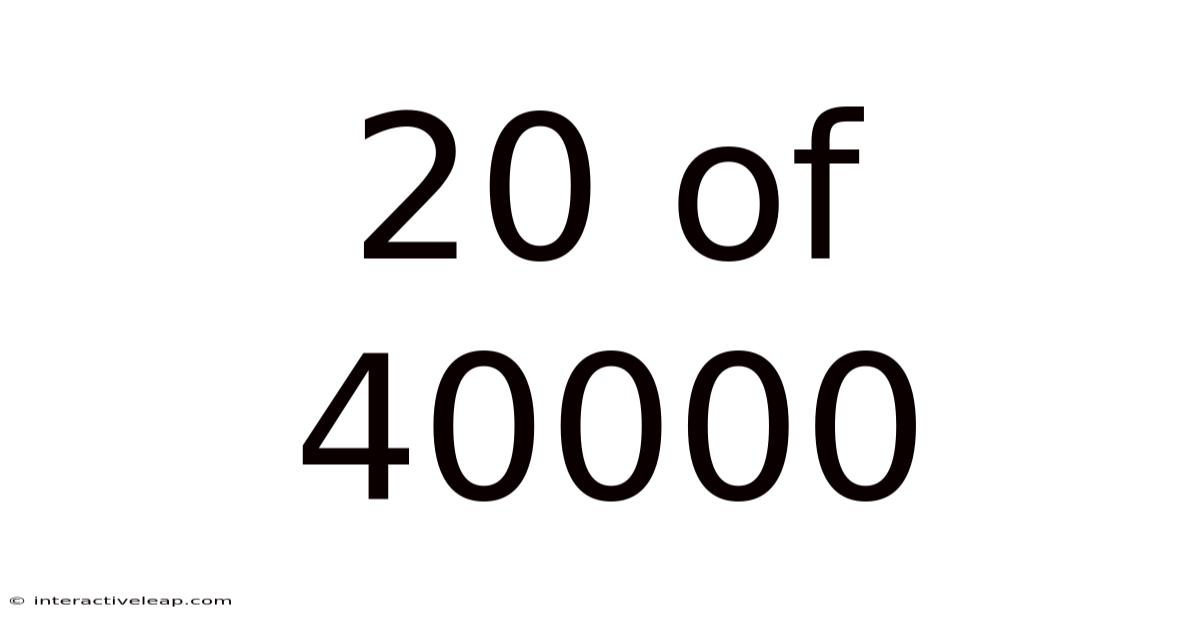
Table of Contents
Decoding 20 out of 40,000: Understanding Proportions, Percentages, and Their Real-World Applications
Understanding proportions and percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific research. This article delves into the seemingly simple calculation of "20 out of 40,000," exploring its meaning, different ways to represent it, and its significance in various contexts. We'll also unpack the underlying mathematical concepts and explore how this type of calculation impacts decision-making in various real-world scenarios.
Understanding the Basics: Fractions, Decimals, and Percentages
Before we dive into the specifics of 20 out of 40,000, let's solidify our understanding of the foundational concepts. The statement "20 out of 40,000" represents a fraction. In mathematical terms, this is written as 20/40,000. This fraction signifies the ratio of a part (20) to a whole (40,000).
We can simplify this fraction by dividing both the numerator (top number) and the denominator (bottom number) by their greatest common divisor, which is 20. This simplifies the fraction to 1/2000.
This fraction can also be expressed as a decimal by performing the division: 1 ÷ 2000 = 0.0005. Finally, this decimal can be converted into a percentage by multiplying by 100: 0.0005 x 100 = 0.05%. Therefore, 20 out of 40,000 represents 1/2000, 0.0005, or 0.05%.
Real-World Applications and Interpretations
The meaning of "20 out of 40,000" is heavily context-dependent. Its significance varies dramatically depending on what those 20 and 40,000 represent. Let's explore a few examples:
-
Manufacturing Defects: Imagine a factory producing 40,000 widgets. If 20 of these widgets are defective, the defect rate is 0.05%. This might seem insignificant, but in a large-scale operation, even a small percentage of defects can translate to significant costs associated with repairs, replacements, and potential customer dissatisfaction. This highlights the importance of quality control procedures.
-
Survey Results: Suppose a survey of 40,000 people was conducted to gauge public opinion on a particular issue. If 20 respondents gave a specific answer, this represents a very small portion of the total sample. While not statistically insignificant, it is important to consider the margin of error and the limitations of extrapolating these results to the entire population. Further analysis would be needed to understand the significance of this result.
-
Lottery Wins: If 20 people out of 40,000 participants win a lottery, the probability of winning would be 0.05%. This illustrates the low likelihood of winning most lotteries. Understanding probability and percentages is crucial for responsible gambling behavior.
-
Medical Trials: In a clinical trial involving 40,000 participants, 20 experiencing a particular side effect represents a low incidence rate. However, even a small percentage can be significant depending on the severity of the side effect. Thorough analysis is critical before drawing conclusions.
-
Environmental Studies: If 20 out of 40,000 tested samples of water show contamination, it still represents a small percentage. However, the location and nature of the contamination would need to be investigated to assess the environmental risk and potential health hazards.
Mathematical Significance and Calculations
The calculation of 20 out of 40,000 is a straightforward application of ratio and proportion. The key is understanding how to express this ratio in different forms (fraction, decimal, percentage) and how to interpret the resulting value in context.
Beyond simple calculations, this scenario also opens doors to explore more complex statistical concepts like:
-
Confidence Intervals: In statistical analyses, particularly surveys, confidence intervals provide a range of values within which the true population parameter is likely to fall. The small percentage (0.05%) obtained from our example would likely have a large confidence interval, reflecting the inherent uncertainty associated with small sample proportions.
-
Hypothesis Testing: The small proportion could be used as a basis for hypothesis testing. This would involve formulating a null hypothesis (e.g., the true proportion of defective widgets is 0%) and comparing it to the observed proportion (0.05%) using statistical tests to determine if the difference is statistically significant.
-
Regression Analysis: If the 40,000 data points represent various inputs and 20 represent a specific outcome, regression analysis could be employed to determine the correlation between the inputs and the outcome.
Expanding on the Concept: Proportions and Scaling
The principles behind understanding "20 out of 40,000" extend far beyond the specific numbers. The core concept involves comparing parts to wholes and understanding the relative magnitude of different quantities. This concept is essential for scaling up or down. For example:
-
Scaling Up: If the defect rate in a small batch of 40,000 widgets is 0.05%, we can extrapolate that a larger production run of 400,000 widgets would likely have around 200 defective widgets (0.05% of 400,000).
-
Scaling Down: Conversely, if we know the overall defect rate in a large batch and want to estimate the number of defective widgets in a smaller sample, we can use proportions to make this calculation.
Frequently Asked Questions (FAQ)
Q1: How do I calculate the percentage of 20 out of 40,000 accurately?
A1: The most accurate way is to use a calculator or spreadsheet software. Divide 20 by 40,000 (20/40000 = 0.0005) and then multiply the result by 100 (0.0005 x 100 = 0.05%).
Q2: Is 0.05% a significant number?
A2: The significance of 0.05% depends entirely on the context. In some situations, it might be negligible, while in others, it could be a cause for serious concern (e.g., a high defect rate in manufacturing).
Q3: Can I use different units to express the proportion (e.g., parts per million)?
A3: Yes, absolutely. 0.05% is equivalent to 50 parts per million (ppm). Using different units can sometimes be more intuitive depending on the context.
Q4: What if the numbers were different? How would I approach a similar problem?
A4: The same principles apply. For any "X out of Y" problem, divide X by Y and multiply by 100 to find the percentage. The interpretation will depend on the context of X and Y.
Conclusion: The Power of Proportions
Understanding proportions, percentages, and their applications is crucial for critical thinking and problem-solving in various aspects of life. The seemingly simple calculation of "20 out of 40,000" provides a gateway to exploring complex mathematical and statistical concepts. The ability to accurately calculate, interpret, and apply these concepts is a valuable skill that enhances decision-making across numerous fields, from quality control to public health and beyond. Remember that the context is key: the numerical result alone doesn't tell the whole story. Always consider the implications of the proportion within its specific context to draw meaningful conclusions.
Latest Posts
Latest Posts
-
20 Off 160
Sep 18, 2025
-
65 In Feet
Sep 18, 2025
-
Shrek And Onions
Sep 18, 2025
-
1200mm In Meters
Sep 18, 2025
-
Sunbeds For Tanning
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 40000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.