65 Of 180
interactiveleap
Sep 18, 2025 · 5 min read
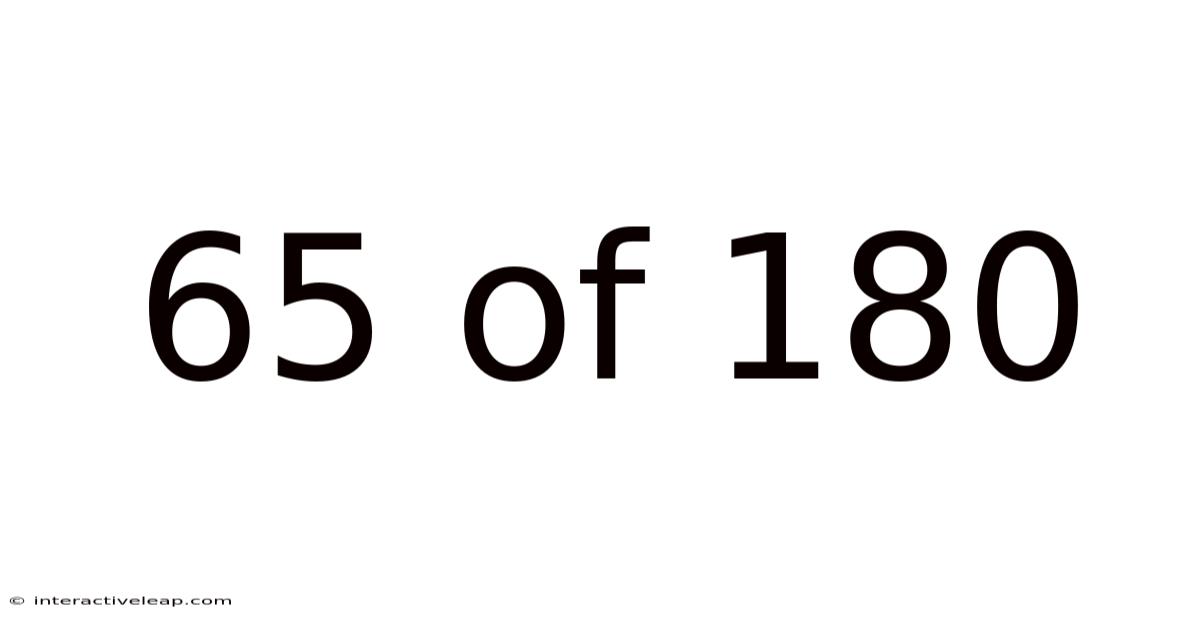
Table of Contents
Decoding the Fraction: Understanding 65/180 and its Implications
The fraction 65/180 might seem like a simple mathematical expression, but understanding its components and implications opens doors to a deeper appreciation of fractions, ratios, and their real-world applications. This article will delve into the intricacies of 65/180, exploring its simplification, decimal representation, percentage equivalent, and various contextual interpretations. We'll also touch upon related mathematical concepts and explore how this seemingly simple fraction can be a powerful tool for understanding more complex ideas.
Understanding Fractions: A Quick Refresher
Before we dive into 65/180, let's briefly review the basics of fractions. A fraction represents a part of a whole. It's composed of two main parts: the numerator (the top number, representing the part) and the denominator (the bottom number, representing the whole). In our case, 65 is the numerator and 180 is the denominator. This means we're considering 65 parts out of a total of 180 parts.
Simplifying 65/180: Finding the Greatest Common Divisor (GCD)
One of the first steps in working with fractions is simplification. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both numbers without leaving a remainder.
To find the GCD of 65 and 180, we can use the Euclidean algorithm or prime factorization. Let's use prime factorization:
- 65: 5 x 13
- 180: 2 x 2 x 3 x 3 x 5
The common prime factor is 5. Therefore, the GCD of 65 and 180 is 5.
Dividing both the numerator and denominator by 5, we get:
65 ÷ 5 = 13 180 ÷ 5 = 36
Therefore, the simplified form of 65/180 is 13/36. This simplified fraction is easier to work with and represents the same proportion as the original fraction.
Converting to Decimal: From Fraction to Decimal Representation
To convert the fraction 13/36 to a decimal, we simply divide the numerator (13) by the denominator (36):
13 ÷ 36 ≈ 0.3611
This means that 65/180, or its simplified form 13/36, is approximately equal to 0.3611. The decimal representation provides another way to understand the magnitude of the fraction.
Calculating the Percentage: Expressing the Fraction as a Percentage
Converting a fraction to a percentage involves multiplying the decimal equivalent by 100. In this case:
0.3611 x 100 ≈ 36.11%
Therefore, 65/180 is approximately 36.11%. Expressing the fraction as a percentage allows for easier comparison with other percentages and provides a more readily understandable representation in many contexts.
Real-World Applications and Contextual Interpretations:
The fraction 65/180, or its simplified version 13/36, can be applied in various real-world scenarios:
-
Test Scores: Imagine a student scoring 65 out of 180 points on a test. Their score would be 13/36 or approximately 36.11%. This gives a clear picture of their performance relative to the total possible points.
-
Proportions and Ratios: The fraction could represent a ratio, such as the ratio of male to female students in a class. If there are 65 male students and 180 total students, then the ratio of male students is 13/36 or approximately 36.11%.
-
Survey Results: The fraction might represent the proportion of respondents who answered "yes" to a particular question in a survey. If 65 out of 180 respondents answered "yes," the proportion is 13/36 or approximately 36.11%.
-
Part-to-Whole Relationships: In any situation involving parts of a whole, such as measuring ingredients in a recipe or analyzing data in a spreadsheet, fractions provide a precise way to represent these relationships.
Further Mathematical Exploration:
Understanding 65/180 opens avenues to exploring more complex mathematical concepts:
-
Equivalent Fractions: Any fraction that simplifies to 13/36 is equivalent to 65/180. For example, 26/72, 39/108, and so on. This highlights the concept of proportional relationships.
-
Improper Fractions and Mixed Numbers: While 65/180 is a proper fraction (numerator less than denominator), understanding how to convert between proper fractions, improper fractions (numerator greater than or equal to denominator), and mixed numbers (whole number and a fraction) is crucial.
-
Fraction Operations: Learning to add, subtract, multiply, and divide fractions is essential for solving a wide range of mathematical problems. Understanding 65/180 provides a solid foundation for mastering these operations.
-
Ratios and Proportions: Fractions are fundamental to understanding ratios and proportions, which are used extensively in geometry, algebra, and other mathematical fields. The relationship between 65 and 180 is a specific instance of a ratio, illustrating the broader concept.
-
Percentage Calculations: The conversion of 65/180 to a percentage demonstrates the importance of understanding percentage calculations, which are widely used in finance, statistics, and everyday life.
Frequently Asked Questions (FAQ):
-
Q: Can 65/180 be simplified further than 13/36?
- A: No. 13 and 36 have no common factors other than 1, meaning 13/36 is in its simplest form.
-
Q: What is the reciprocal of 65/180?
- A: The reciprocal is found by swapping the numerator and the denominator. The reciprocal of 65/180 (or 13/36) is 180/65 (or 36/13).
-
Q: How would I add 65/180 to another fraction?
- A: You would first need to find a common denominator for both fractions before adding the numerators. Simplifying the fractions beforehand often makes this process easier.
-
Q: What are some real-world examples where this fraction could appear?
- A: Many scenarios involve ratios or proportions, including those mentioned earlier: test scores, survey results, ingredient ratios in recipes, and various data analysis contexts.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to work with, understand, and compare. It also allows for clearer visualization of the proportion they represent.
Conclusion:
While initially appearing simple, the fraction 65/180 offers a rich landscape for exploring fundamental mathematical concepts. Understanding its simplification, decimal and percentage equivalents, and potential real-world applications strengthens one's grasp of fractions, ratios, and their significance in various fields. By exploring the properties of this single fraction, we've touched upon core mathematical ideas that form the foundation for more advanced mathematical studies. This deeper understanding not only enhances problem-solving skills but also cultivates a greater appreciation for the elegance and practicality of mathematics. The seemingly mundane fraction 65/180, therefore, serves as a microcosm of the broader mathematical world, offering a valuable learning opportunity for students and enthusiasts alike.
Latest Posts
Latest Posts
-
20 Off 160
Sep 18, 2025
-
65 In Feet
Sep 18, 2025
-
Shrek And Onions
Sep 18, 2025
-
1200mm In Meters
Sep 18, 2025
-
Sunbeds For Tanning
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 65 Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.