60 Of 230
interactiveleap
Sep 18, 2025 · 5 min read
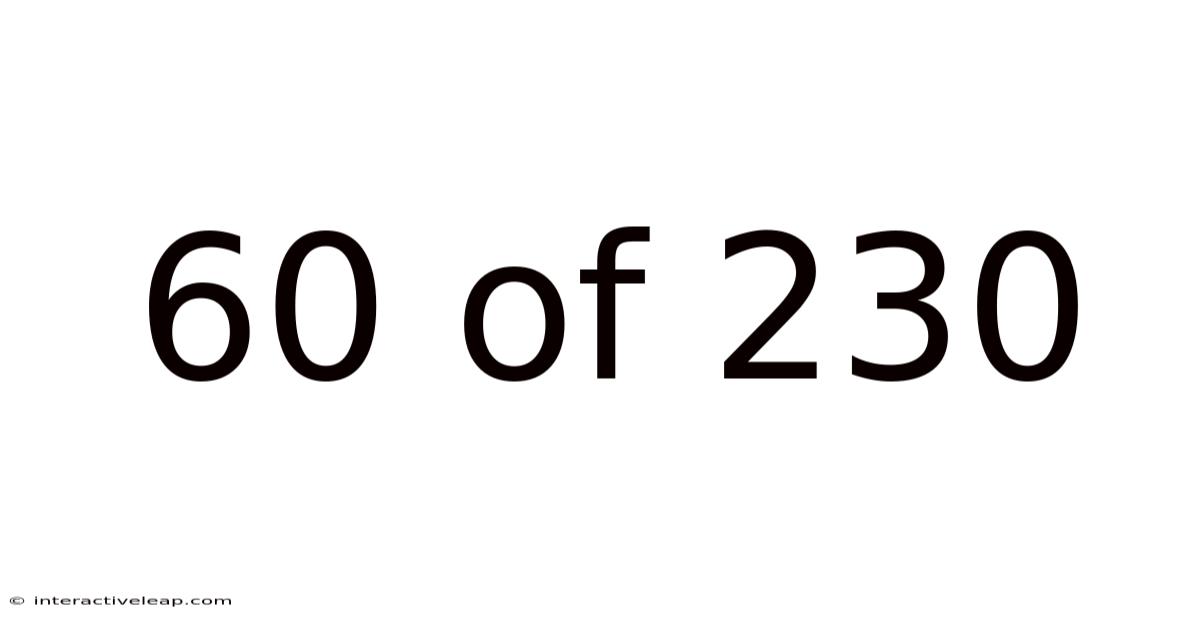
Table of Contents
Understanding the Fraction 60/230: Simplification, Decimal Conversion, and Real-World Applications
The fraction 60/230 might seem daunting at first glance, especially for those less comfortable with mathematical concepts. However, understanding this fraction – simplifying it, converting it to a decimal, and exploring its real-world applications – is surprisingly straightforward and highly valuable for building a strong foundation in mathematics. This article will guide you through the process step-by-step, ensuring you grasp not only the mechanics but also the underlying principles.
Introduction: Deconstructing the Fraction 60/230
The fraction 60/230 represents a part of a whole. The number 60 is the numerator, indicating the number of parts we have, while 230 is the denominator, indicating the total number of equal parts that make up the whole. Our goal is to understand this relationship better, which involves simplification, decimal conversion, and exploring its practical implications. This knowledge is crucial in various fields, from basic arithmetic and algebra to more advanced applications in science, engineering, and finance.
1. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we delve into other aspects, simplifying the fraction is essential. Simplification makes the fraction easier to understand and work with. This involves finding the Greatest Common Divisor (GCD) of both the numerator (60) and the denominator (230). The GCD is the largest number that divides both 60 and 230 without leaving a remainder.
To find the GCD, we can use the Euclidean algorithm or prime factorization. Let's use prime factorization:
- Prime factorization of 60: 2 x 2 x 3 x 5 = 2² x 3 x 5
- Prime factorization of 230: 2 x 5 x 23
By comparing the prime factorizations, we can see that the common factors are 2 and 5. Therefore, the GCD is 2 x 5 = 10.
Now, we divide both the numerator and the denominator by the GCD:
60 ÷ 10 = 6 230 ÷ 10 = 23
Therefore, the simplified fraction is 6/23. This simplified form represents the same value as 60/230 but is much more manageable.
2. Converting the Fraction to a Decimal: Understanding the Relationship
Converting a fraction to a decimal involves dividing the numerator by the denominator. In our case, we'll divide 6 by 23:
6 ÷ 23 ≈ 0.260869565...
This results in a non-terminating decimal, meaning the decimal representation goes on infinitely without repeating. For practical purposes, we often round the decimal to a specific number of decimal places. Rounding to three decimal places, we get 0.261. This decimal representation provides a different way of understanding the relative size of the fraction.
3. Real-World Applications: Visualizing and Understanding Proportions
The fraction 60/230 (or its simplified form 6/23) finds numerous applications in various real-world scenarios. Let's explore a few examples:
-
Proportions and Ratios: Imagine you have a bag containing 60 red marbles and 170 blue marbles (60 + 170 = 230 total marbles). The fraction 60/230 represents the proportion of red marbles in the bag. The simplified fraction 6/23 indicates that for every 23 marbles, 6 are red. This concept of proportion and ratio is fundamental in many areas, including statistics, chemistry (mixing solutions), and cooking (following recipes).
-
Percentages: To convert the fraction to a percentage, we multiply the decimal representation by 100: 0.261 x 100 = 26.1%. This means that 60/230 represents approximately 26.1% of the whole. Percentages are commonly used to express proportions in various contexts, including finance (interest rates), sales (discounts), and test scores.
-
Probability: If an event has a probability of 60/230 (or 6/23), it means that out of 230 possible outcomes, 60 are favorable. This is crucial in understanding risk and chance in fields like gambling, insurance, and scientific experiments.
-
Measurements and Scaling: Imagine you are working on a scale model. If the scale is 1:23, and a part on the real object measures 6 units, then the corresponding measurement on the model would be 6/23 units. This concept is fundamental in architecture, engineering, and cartography.
4. Further Exploration: Working with Fractions
Understanding 60/230 provides a foundation for working with more complex fractions. Here are some related concepts to explore:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have the same denominator (a common denominator). If the denominators are different, you need to find the least common multiple (LCM) to make them equal.
-
Multiplying and Dividing Fractions: Multiplying fractions is relatively straightforward; you multiply the numerators and the denominators separately. Dividing fractions involves inverting the second fraction and then multiplying.
-
Improper Fractions and Mixed Numbers: An improper fraction is one where the numerator is larger than the denominator (e.g., 23/6). An improper fraction can be converted to a mixed number (e.g., 3 5/6), which consists of a whole number and a fraction.
5. Frequently Asked Questions (FAQ)
-
Q: Why is simplification important?
- A: Simplification makes fractions easier to understand and work with. It reduces the numbers involved, making calculations simpler and reducing the risk of errors.
-
Q: What if I don't have a calculator?
- A: You can perform long division to convert a fraction to a decimal. While it might take longer, it's a valuable skill to have.
-
Q: Can I use a different method to find the GCD?
- A: Yes, the Euclidean algorithm is another effective method for finding the greatest common divisor.
-
Q: Are there online tools to simplify fractions?
- A: Yes, many online calculators and websites can simplify fractions automatically.
6. Conclusion: Mastering Fractions: A Stepping Stone to Success
Understanding the fraction 60/230, from its simplification to its decimal conversion and real-world applications, is a significant step in developing your mathematical skills. This seemingly simple fraction embodies fundamental concepts that are crucial for tackling more complex problems in various fields. By mastering the techniques presented in this article, you'll not only improve your mathematical abilities but also enhance your problem-solving skills, making you better equipped to tackle challenges in various aspects of life. Remember that consistent practice and a curious mindset are key to mastering fractions and other mathematical concepts. The journey of learning is continuous; embrace the challenges, and your understanding will grow exponentially.
Latest Posts
Latest Posts
-
20 Off 160
Sep 18, 2025
-
65 In Feet
Sep 18, 2025
-
Shrek And Onions
Sep 18, 2025
-
1200mm In Meters
Sep 18, 2025
-
Sunbeds For Tanning
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 60 Of 230 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.