5 Of 220
interactiveleap
Sep 18, 2025 · 6 min read
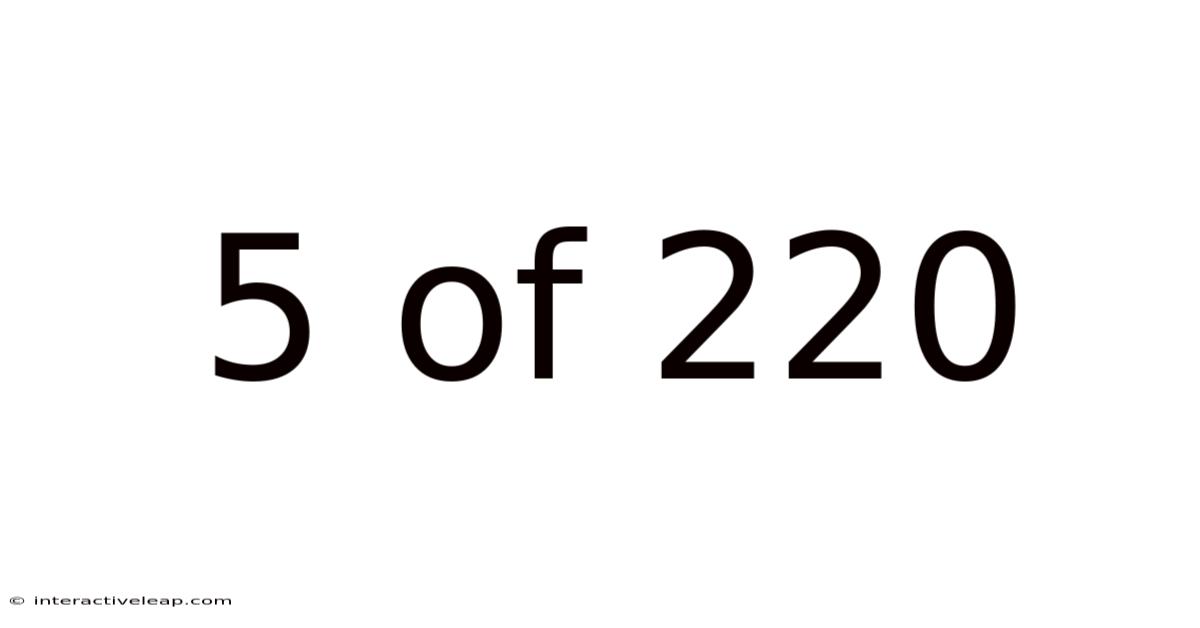
Table of Contents
Decoding the Enigma: Understanding the Significance of 5 of 220 in Probability and Statistics
The seemingly simple expression "5 of 220" hides a rich tapestry of statistical concepts and practical applications. This seemingly innocuous phrase, often encountered in probability calculations, combinatorics problems, and even real-world scenarios like lottery drawings or quality control, actually represents a powerful tool for understanding chance and likelihood. This article will delve deep into the meaning of "5 of 220," exploring its mathematical foundation, practical implications, and demonstrating its relevance across various fields. We will unravel the complexities, providing clear explanations and practical examples for a thorough understanding.
Introduction: What Does "5 of 220" Mean?
In the context of probability and combinatorics, "5 of 220" refers to the number of ways to choose 5 items from a set of 220 distinct items, where the order of selection does not matter. This is a classic combination problem, denoted as ²²⁰C₅ or C(220, 5). This mathematical concept has far-reaching consequences in various fields, ranging from statistical analysis to gaming and even theoretical physics. Understanding this fundamental concept opens doors to understanding more complex probabilistic scenarios.
Understanding Combinations: The Mathematical Foundation
The core concept behind "5 of 220" lies in the field of combinatorics, specifically combinations. A combination is a selection of items from a larger set where the order of selection doesn't matter. This differs from permutations, where the order does matter. For example, choosing three colors from a set of five (red, blue, green, yellow, orange) is a combination, because selecting red, blue, then green is the same as selecting green, blue, then red.
The formula for calculating combinations is:
nCr = n! / (r! * (n-r)!)
Where:
- n is the total number of items (in our case, 220)
- r is the number of items to choose (in our case, 5)
- ! denotes the factorial (e.g., 5! = 5 * 4 * 3 * 2 * 1)
Let's apply this to "5 of 220":
²²⁰C₅ = 220! / (5! * (220-5)!) = 220! / (5! * 215!)
Calculating this directly using a standard calculator would be computationally intensive, even for a powerful machine. Fortunately, most scientific calculators and mathematical software packages have built-in functions for calculating combinations. The result is a remarkably large number: 2,634,967,881,080
This substantial number signifies the vast number of possible combinations when selecting 5 items from a set of 220. This highlights the immense possibilities inherent in even seemingly simple selection processes.
Step-by-Step Calculation (Illustrative Example with Smaller Numbers)
While calculating ²²⁰C₅ directly is complex, understanding the process is crucial. Let's illustrate with a smaller example: choosing 2 items from a set of 4 (A, B, C, D).
-
List all possibilities: AB, AC, AD, BC, BD, CD
-
Count the possibilities: There are 6 possible combinations.
-
Apply the formula: ⁴C₂ = 4! / (2! * 2!) = (4 * 3 * 2 * 1) / ((2 * 1) * (2 * 1)) = 6
This simple example demonstrates how the formula works. While we cannot practically list all combinations for 5 of 220, the formula provides a precise way to determine the total number of possibilities.
Practical Applications: Real-World Scenarios
The concept of "5 of 220" and combinations in general, has widespread applications:
-
Lottery Calculations: Many lottery systems involve selecting a specific number of balls from a larger pool. Calculating the odds of winning often involves calculating combinations. For example, a lottery where you choose 5 numbers from a pool of 220 would have incredibly long odds, based on the vast number of possible combinations.
-
Quality Control: In manufacturing, sampling techniques are often used to assess the quality of a large batch of products. Selecting a sample of 5 items from a batch of 220 to test for defects involves combinations.
-
Card Games: Certain card games involve selecting a hand of cards from a deck. The probability of getting a specific hand can be determined using combinations.
-
Genetics and Bioinformatics: In genetics, combinations are used to model the different possible genotypes that can arise from a set of alleles.
-
Experimental Design: When designing experiments, researchers often need to select subsets of individuals or conditions from a larger pool. Combinatorics helps determine the number of possible experimental configurations.
Beyond the Numbers: Understanding Probability and Odds
While the number 2,634,967,881,080 represents the total number of combinations for "5 of 220," understanding the probability of selecting a specific combination requires further calculation. Probability is expressed as the ratio of favorable outcomes to the total number of possible outcomes. For instance, the probability of winning a lottery where you need to select the exact 5 numbers from 220 would be 1 in 2,634,967,881,080. This illustrates the incredibly low probability of winning such a lottery.
This understanding of probability goes beyond simply knowing the number of combinations. It provides a crucial framework for risk assessment, decision-making under uncertainty, and even understanding complex systems.
Frequently Asked Questions (FAQs)
-
Q: What if the order of selection matters? A: If the order matters, we'd be dealing with permutations, not combinations. The number of permutations would be significantly larger than the number of combinations.
-
Q: How can I calculate ²²⁰C₅ without specialized software? A: For such large numbers, using a calculator or software with a combination function (often denoted as nCr or C(n,r)) is necessary. Manual calculation using the factorial formula is impractical due to the size of the numbers involved.
-
Q: What are some real-world examples beyond those mentioned? A: Combinations find use in various fields, including network security (analyzing password possibilities), marketing (selecting target audiences), and even social science (analyzing social networks).
-
Q: Can this concept be extended to larger numbers? A: Absolutely. The combination formula applies to any positive integers n and r, where n ≥ r.
Conclusion: The Power of "5 of 220"
The seemingly simple phrase "5 of 220" encapsulates a powerful concept in probability and statistics. It represents a large number of possibilities, illustrating the vastness of potential outcomes in various selection processes. Understanding combinations, the underlying mathematical principle, allows us to calculate the probability of specific events, assess risk, and make informed decisions. From lottery calculations to quality control, genetics to experimental design, the application of this concept extends across numerous disciplines. While calculating the exact number may require computational assistance, grasping the fundamental concept empowers us to understand the role of chance and likelihood in the world around us. This foundational knowledge is essential for anyone seeking to analyze data, make predictions, or simply appreciate the sheer scale of possibilities inherent in seemingly simple choices. The seemingly simple act of choosing 5 items from 220 unveils a universe of mathematical possibilities, highlighting the intricate beauty and practicality of combinatorics.
Latest Posts
Latest Posts
-
25 Divided 7
Sep 19, 2025
-
67 X 3
Sep 19, 2025
-
Jojo Star Tattoo
Sep 19, 2025
-
Scheduled For Today
Sep 19, 2025
-
4 5 X 400
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 Of 220 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.