4/5 X 400
interactiveleap
Sep 19, 2025 · 6 min read
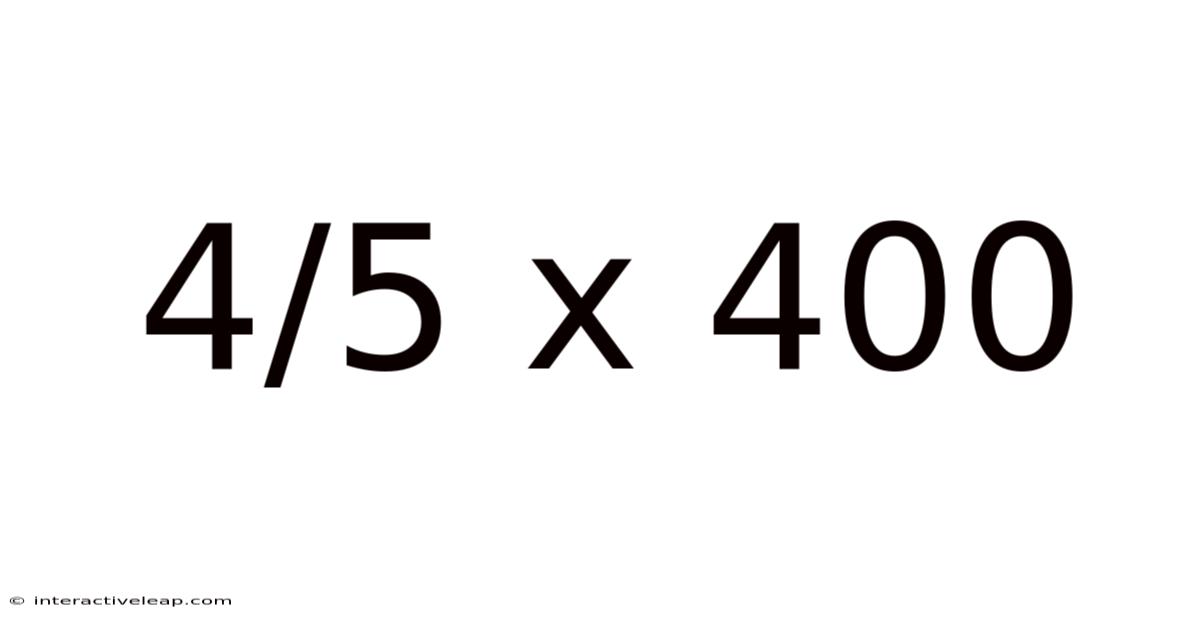
Table of Contents
Decoding 4/5 x 400: A Deep Dive into Fractions and Multiplication
This article explores the seemingly simple calculation of 4/5 x 400, delving beyond the immediate answer to illuminate the underlying principles of fraction multiplication and its real-world applications. We'll break down the process step-by-step, explore different methods of solving the problem, and discuss the broader mathematical concepts involved. This comprehensive guide is perfect for students looking to solidify their understanding of fractions and anyone interested in exploring the beauty and practicality of mathematics.
Understanding the Problem: 4/5 x 400
The problem, 4/5 x 400, presents a straightforward multiplication of a fraction (4/5) and a whole number (400). At its core, it asks: "What is four-fifths of 400?" This seemingly simple question opens the door to understanding fundamental concepts in arithmetic, particularly the manipulation of fractions.
Method 1: Converting the Whole Number to a Fraction
One effective approach involves converting the whole number, 400, into a fraction. Any whole number can be expressed as a fraction by placing it over 1. Therefore, 400 becomes 400/1. Our problem now transforms into:
(4/5) x (400/1)
To multiply fractions, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(4 x 400) / (5 x 1) = 1600 / 5
Now we simplify the resulting fraction by dividing the numerator by the denominator:
1600 / 5 = 320
Therefore, 4/5 x 400 = 320
Method 2: Simplifying Before Multiplying
This method leverages the commutative and associative properties of multiplication, allowing us to simplify the calculation before performing the multiplication. We can rewrite the equation as:
4 x (400/5)
Notice that we've grouped 400/5. This simplifies the calculation considerably. Dividing 400 by 5 gives us 80:
4 x 80 = 320
This method highlights the importance of identifying opportunities for simplification to make calculations easier and less prone to errors.
Method 3: Using Decimals
Another approach involves converting the fraction 4/5 into its decimal equivalent. Dividing 4 by 5 gives us 0.8. The problem then becomes:
0.8 x 400
Multiplying 0.8 by 400 yields:
0.8 x 400 = 320
This method demonstrates the interchangeability between fractions and decimals, highlighting the versatility of different mathematical representations.
The Real-World Application of Fraction Multiplication
The calculation 4/5 x 400 isn't just an abstract mathematical exercise; it has numerous real-world applications. Consider these examples:
-
Sales and Discounts: Imagine a store offering a 20% discount on an item priced at $400. A 20% discount is equivalent to 1/5 (or 20/100 simplified). Therefore, the discount amount can be calculated as (1/5) x 400 = $80. The final price would be $400 - $80 = $320. This is directly related to our initial problem, where 4/5 represents the remaining 80% after the discount.
-
Recipe Scaling: If a recipe calls for 400 grams of flour and you only want to make 4/5 of the recipe, you would use (4/5) x 400 = 320 grams of flour.
-
Measurement Conversion: Imagine needing to convert 400 inches into feet. Since there are 12 inches in a foot, each inch is 1/12 of a foot. To find the length in feet, one might need a calculation involving fractions. While this example is not directly 4/5 x 400, it shows the relevance of fraction multiplication in various measurement conversions.
-
Project Completion: If a project is expected to take 400 hours and you've completed 4/5 of it, you've finished (4/5) x 400 = 320 hours of work.
Understanding Fractions: A Deeper Dive
To truly grasp the calculation 4/5 x 400, it's crucial to understand the fundamental concepts of fractions.
-
Numerator and Denominator: A fraction consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator represents the number of parts you have, while the denominator represents the total number of equal parts in a whole.
-
Equivalent Fractions: Many fractions can represent the same value. For example, 1/2, 2/4, and 4/8 are all equivalent fractions. Understanding equivalent fractions is crucial for simplifying calculations and comparing fractions.
-
Simplifying Fractions: Simplifying a fraction means reducing it to its lowest terms. This is done by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, 1600/5 can be simplified by dividing both by 5, resulting in 320/1, which is equivalent to 320.
-
Improper Fractions and Mixed Numbers: An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4). A mixed number combines a whole number and a fraction (e.g., 1 1/4). It's often helpful to convert between improper fractions and mixed numbers depending on the context of the problem.
Frequently Asked Questions (FAQ)
Q1: Why is multiplying fractions different from adding or subtracting them?
A1: When adding or subtracting fractions, you need a common denominator. Multiplication of fractions is simpler; you multiply numerators together and denominators together directly.
Q2: Can I use a calculator to solve 4/5 x 400?
A2: Yes, absolutely. Most calculators can handle fraction multiplication directly, or you can convert the fraction to a decimal before multiplying.
Q3: What if the fraction was more complex, like 17/23 x 400?
A3: The same principles apply. You would multiply the numerators and the denominators, then simplify the resulting fraction. In such cases, a calculator might be more efficient.
Q4: Is there a visual way to understand 4/5 x 400?
A4: Yes, you could imagine a rectangle representing 400 units. Divide this rectangle into 5 equal parts. Four of those five parts represent 4/5 of 400. Counting the units in those four parts would give you the answer, 320.
Conclusion: Mastering Fractions and Multiplication
The seemingly simple calculation of 4/5 x 400 provides a valuable opportunity to explore fundamental mathematical concepts. By understanding different methods of solving the problem, including converting to decimals, simplifying fractions before multiplication, and visualizing the problem, we can develop a more profound appreciation for the interconnectedness of arithmetic principles. This knowledge extends far beyond the classroom, finding practical applications in diverse fields, from finance and cooking to project management and beyond. The ability to confidently solve problems involving fractions is a cornerstone of mathematical literacy and a valuable skill in navigating the complexities of daily life. Remember, the key lies not just in finding the answer (320) but in understanding why that answer is correct and how it relates to broader mathematical principles.
Latest Posts
Latest Posts
-
Double Eagle Coin
Sep 19, 2025
-
4 5 X 5
Sep 19, 2025
-
20 Of 625
Sep 19, 2025
-
36 2c To F
Sep 19, 2025
-
2x 3 2
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 4/5 X 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.