2x 3 2
interactiveleap
Sep 19, 2025 · 6 min read
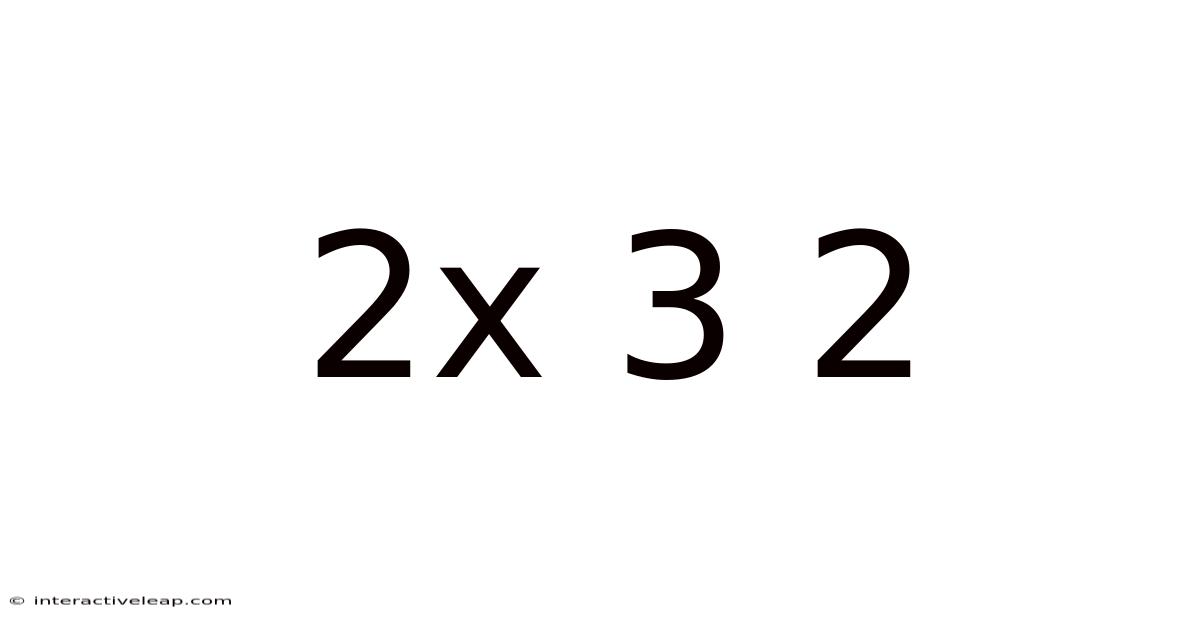
Table of Contents
Decoding the Enigma: A Deep Dive into 2 x 3 x 2
The seemingly simple expression "2 x 3 x 2" might appear trivial at first glance. However, this seemingly basic mathematical statement opens doors to exploring fundamental concepts in arithmetic, algebra, and even touches upon broader applications in various fields. This article will dissect this expression, examining its straightforward calculation, delving into its underlying principles, and exploring its implications within a wider mathematical context. We’ll cover everything from basic multiplication to more advanced applications, making this a comprehensive guide suitable for learners of all levels.
Understanding Basic Multiplication: The Foundation of 2 x 3 x 2
Before tackling the complexities (or lack thereof!) of 2 x 3 x 2, let's establish a firm understanding of multiplication itself. Multiplication is essentially repeated addition. For example, 2 x 3 means adding two three times: 2 + 2 + 2 = 6. Similarly, 3 x 2 means adding three two times: 3 + 3 = 6. This fundamental principle underpins all multiplication operations, regardless of complexity.
Now, let’s tackle our primary expression: 2 x 3 x 2. Following the order of operations (often remembered by the acronym PEMDAS/BODMAS – Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction), we perform multiplication from left to right:
- 2 x 3 = 6
- 6 x 2 = 12
Therefore, the solution to 2 x 3 x 2 is 12. This simple calculation forms the bedrock for more intricate mathematical operations.
Exploring the Commutative and Associative Properties: Rearranging the Equation
Multiplication possesses two key properties that allow us to manipulate the equation without altering the result:
-
Commutative Property: The order of the numbers in a multiplication equation doesn't affect the product. This means 2 x 3 x 2 is the same as 2 x 2 x 3, 3 x 2 x 2, and so on. The result remains 12.
-
Associative Property: The way we group numbers in a multiplication equation doesn't change the product. We can group the numbers as (2 x 3) x 2 or 2 x (3 x 2), and the result remains 12. This property allows for flexibility in calculations.
These properties are fundamental in simplifying more complex calculations, particularly those involving numerous factors. Understanding them allows for strategic grouping and reordering of numbers to make calculations easier and more efficient.
Beyond Basic Arithmetic: Applications in Algebra and Beyond
While 2 x 3 x 2 might seem a trivial problem in arithmetic, its principles extend to far more complex mathematical areas:
-
Algebra: Consider a simple algebraic expression: 2x * 3y * 2z. While we can't simplify the variables (x, y, z), we can still apply the same principles of multiplication to the coefficients (the numbers in front of the variables). This simplifies to 12xyz, demonstrating the direct application of the arithmetic principles to algebraic manipulation.
-
Geometry: Imagine calculating the volume of a rectangular prism (a box). If the dimensions are 2 units, 3 units, and 2 units, the volume is calculated by multiplying these dimensions together: 2 x 3 x 2 = 12 cubic units. This showcases the practical application of this simple calculation in real-world scenarios.
-
Computer Science: In programming, multiplication is a fundamental operation. The calculation 2 x 3 x 2 might appear within loops, array manipulations, or even more complex algorithms. The efficiency of such calculations is crucial for the performance of computer programs.
-
Probability and Statistics: The concept of permutations and combinations relies heavily on multiplication. For example, calculating the number of possible arrangements of three objects (2 choices for the first, 3 for the second, and 2 for the third) uses the same principle: 2 x 3 x 2 = 12 possible arrangements.
-
Physics and Engineering: Many physical laws and engineering formulas incorporate multiplication. Calculations involving force, velocity, acceleration, and many other physical quantities frequently involve multiplying various factors. Even seemingly simple problems often involve a series of multiplications similar to 2 x 3 x 2.
Expanding the Concept: Exploring Larger Numbers and Patterns
While we've focused on the relatively small numbers in 2 x 3 x 2, the principles remain consistent with larger numbers. Consider 15 x 22 x 3: We would still follow the order of operations (performing multiplication from left to right) to arrive at the correct answer. The commutative and associative properties are equally applicable to these larger numbers. This reinforces the universality of the principles explored in this seemingly basic example.
The Significance of Order of Operations: Avoiding Miscalculations
The order of operations is crucial for obtaining the correct result. Without adhering to PEMDAS/BODMAS, we could arrive at different – and incorrect – results. For example, if we perform the calculation 2 x (3 + 2) instead of 2 x 3 x 2, the result would be 10, highlighting the critical role of adhering to established mathematical rules.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers were different? How would I solve 4 x 5 x 6?
A: The principles remain the same. You'd perform the multiplications from left to right: 4 x 5 = 20, then 20 x 6 = 120.
-
Q: Can I use a calculator to solve 2 x 3 x 2?
A: Absolutely! Calculators are excellent tools for performing calculations quickly and accurately, even for seemingly simple expressions like this one.
-
Q: What is the importance of understanding the commutative and associative properties?
A: These properties are vital for simplifying complex calculations and making them more manageable. They allow you to rearrange and group numbers strategically, making calculations easier and less prone to errors.
-
Q: Are there any real-world examples beyond what's already mentioned?
A: Yes! Consider baking a cake. If a recipe calls for 2 cups of flour, 3 eggs, and 2 teaspoons of vanilla, you're essentially using multiplication to scale the recipe (e.g., doubling it would mean 2 x 2 cups flour, 2 x 3 eggs, 2 x 2 teaspoons vanilla).
Conclusion: The Unassuming Power of 2 x 3 x 2
While seemingly insignificant, the expression "2 x 3 x 2" embodies the fundamental principles of arithmetic, extends into advanced mathematical fields, and finds countless applications in various disciplines. Understanding this simple calculation is not merely about getting the answer (12), but about grasping the underlying principles that govern mathematical operations and their widespread relevance in the world around us. From the basics of multiplication to the intricacies of algebra and beyond, this expression serves as a microcosm of the power and elegance of mathematics. Its simplicity belies its profound significance, underscoring the importance of even the most fundamental concepts in building a strong foundation for mathematical understanding.
Latest Posts
Latest Posts
-
1 8kg In Lbs
Sep 19, 2025
-
Examen In English
Sep 19, 2025
-
1 5cm In Mm
Sep 19, 2025
-
2000 X 6
Sep 19, 2025
-
Bruegel Peasant Wedding
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2x 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.