2000 X 6
interactiveleap
Sep 19, 2025 · 6 min read
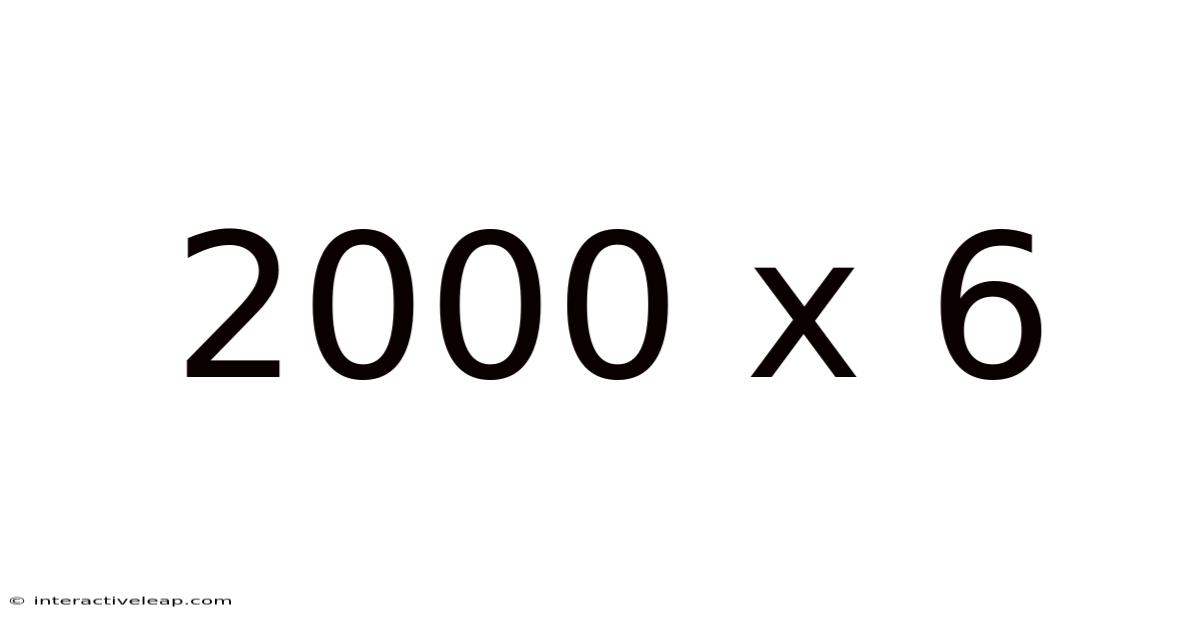
Table of Contents
Exploring the Mathematical Landscape of 2000 x 6: A Deep Dive into Multiplication
This article delves into the seemingly simple yet surprisingly rich mathematical landscape surrounding the multiplication problem 2000 x 6. We'll explore different methods of solving this, examine the underlying principles, and uncover some interesting connections to broader mathematical concepts. Understanding this seemingly basic calculation opens doors to a deeper appreciation of arithmetic and its applications in everyday life.
Introduction: More Than Just a Calculation
At first glance, 2000 x 6 appears straightforward. It's a basic multiplication problem that many learn in elementary school. However, a deeper exploration reveals layers of mathematical understanding that extend far beyond simply obtaining the answer. This problem provides a fantastic opportunity to revisit fundamental concepts like place value, the distributive property, and the commutative property, reinforcing a strong foundation in arithmetic. Furthermore, it acts as a stepping stone to understanding more complex multiplication problems and related areas like algebra.
Method 1: The Standard Algorithm
The most common method for solving 2000 x 6 is the standard multiplication algorithm taught in schools. This involves multiplying each digit of the first number (2000) by the second number (6), starting from the rightmost digit and carrying over any tens. However, in this specific case, the simplicity of 2000 makes this process exceptionally efficient.
- Multiply the ones place: 0 x 6 = 0
- Multiply the tens place: 0 x 6 = 0
- Multiply the hundreds place: 0 x 6 = 0
- Multiply the thousands place: 2 x 6 = 12
Therefore, the result is 12000. This method emphasizes place value – understanding that the 2 in 2000 represents 2000 and not simply 2.
Method 2: The Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this property to break down 2000 x 6 into smaller, more manageable parts. We can express 2000 as 2000 = 2000 + 0.
Applying the distributive property:
6 x 2000 = 6 x (2000 + 0) = (6 x 2000) + (6 x 0) = 12000 + 0 = 12000
This method highlights the fundamental principle that multiplication is essentially repeated addition. We are adding 2000 six times. This approach is particularly helpful when dealing with larger numbers and demonstrates the power of breaking complex problems into simpler components.
Method 3: Breaking Down the Numbers
We can simplify the calculation by breaking down 2000 into smaller, more easily manageable numbers. For instance, we can break 2000 down into 2 x 1000:
(2 x 1000) x 6
Using the associative property of multiplication (which states that (a x b) x c = a x (b x c)), we can rearrange the equation:
2 x (1000 x 6) = 2 x 6000 = 12000
This method demonstrates the flexibility and efficiency of applying mathematical properties to simplify calculations. It also reinforces the understanding of multiples of 10, 100, and 1000, which are crucial for efficient mental arithmetic and estimation.
Method 4: Mental Math Techniques
With practice, many multiplication problems can be solved mentally. For 2000 x 6, a simple mental math technique involves recognizing that multiplying by 6 is the same as multiplying by 2 and then by 3.
- Multiply by 2: 2000 x 2 = 4000
- Multiply by 3: 4000 x 3 = 12000
This highlights the usefulness of breaking down complex problems into simpler steps. This approach builds computational fluency and reduces reliance on written calculations.
Real-World Applications: Beyond the Classroom
The multiplication problem 2000 x 6, although seemingly abstract, has practical applications in various real-world scenarios. Consider these examples:
- Manufacturing: A factory produces 2000 units of a product per day. The total production over 6 days can be calculated as 2000 x 6 = 12000 units.
- Finance: Calculating the total cost of 6 items priced at $2000 each involves the same multiplication.
- Agriculture: A farmer has 2000 plants per acre, and the total number of plants across 6 acres would be 12000.
- Construction: Calculating the total number of bricks needed for a project requiring 2000 bricks per section and spanning 6 sections results in 12000 bricks.
These examples show how even basic mathematical concepts have far-reaching implications in diverse fields.
Exploring Related Concepts: Extending Understanding
Understanding 2000 x 6 provides a foundation for exploring more complex mathematical concepts:
- Powers of 10: This problem reinforces the understanding of place value and how multiplying by powers of 10 (10, 100, 1000, etc.) shifts the decimal point.
- Algebra: The problem can be represented algebraically as 2000x = 12000, where 'x' represents the unknown multiplier (6). This transition from arithmetic to algebra is a crucial step in mathematical development.
- Estimation: The problem allows practice in estimating the answer. Recognizing that 2000 is close to 2000 and 6 is a reasonably small multiplier helps quickly generate an approximate answer. This is a crucial skill for real-world problem-solving.
- Order of Operations: This simple problem implicitly demonstrates the order of operations, even though there are no other operations present. Understanding the order of operations is crucial as mathematical complexity increases.
Understanding these related concepts expands the knowledge base beyond simply solving a single multiplication problem.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to learn different methods for solving multiplication problems?
- A: Learning multiple methods provides a deeper understanding of the underlying mathematical principles and enhances problem-solving skills. It also allows you to choose the most efficient method depending on the specific problem.
-
Q: What if I want to multiply 2000 by a larger number, like 60 or 600?
- A: This can be solved using the same principles, either by applying the standard algorithm or by breaking down the numbers into smaller, manageable components and utilizing the distributive property. The key is understanding the place value of the numbers.
-
Q: How can I improve my mental math skills?
- A: Consistent practice is key. Start with simpler problems and gradually increase the complexity. Focus on understanding the underlying principles and applying various mental math techniques.
-
Q: Are there any online resources that can help me practice multiplication?
- A: Many educational websites and apps offer interactive games and exercises to practice multiplication skills.
Conclusion: The Enduring Value of Basic Arithmetic
While 2000 x 6 might seem like a simple multiplication problem, a thorough exploration reveals its richness and significance. It underscores the importance of a solid foundation in basic arithmetic, illustrating fundamental mathematical principles like place value, the distributive property, and the commutative property. Furthermore, it provides a stepping stone to more advanced concepts in algebra and beyond, demonstrating the practical relevance of mathematics in everyday life. Mastering this seemingly simple calculation empowers individuals with enhanced mathematical skills applicable across diverse fields. The value of understanding basic arithmetic like this multiplication problem extends far beyond the classroom, shaping problem-solving abilities and fostering a deeper appreciation for the interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
Beverly Polo Hills
Sep 19, 2025
-
0 7 X 0 5
Sep 19, 2025
-
52 3kg In Stone
Sep 19, 2025
-
Four Thousand Pounds
Sep 19, 2025
-
40 Off 65
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2000 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.