20 Of 625
interactiveleap
Sep 19, 2025 · 6 min read
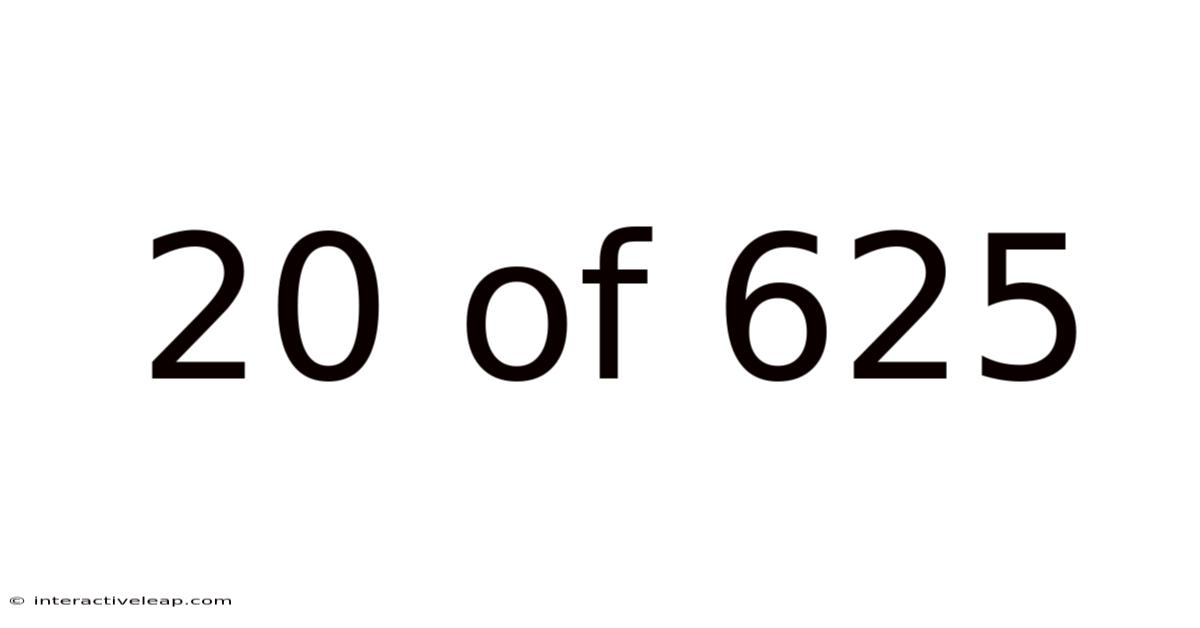
Table of Contents
Unveiling the Mysteries of 20/625: A Deep Dive into Fraction Simplification, Ratios, and Real-World Applications
The seemingly simple fraction 20/625 might appear insignificant at first glance. However, exploring this fraction opens a door to understanding fundamental mathematical concepts like simplification, ratios, and their broad applications in everyday life. This article will guide you through a comprehensive exploration of 20/625, delving into its simplification, equivalent representations, practical applications, and addressing common questions. Understanding this seemingly basic fraction provides a solid foundation for more complex mathematical operations and problem-solving.
Understanding Fractions: A Quick Refresher
Before we embark on our journey with 20/625, let's briefly recap the basics of fractions. A fraction represents a part of a whole. It consists of two main components: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 1/4, the numerator (1) represents one part, and the denominator (4) signifies that the whole is divided into four equal parts.
Simplifying 20/625: Finding the Greatest Common Divisor (GCD)
Simplifying a fraction means reducing it to its lowest terms. This is achieved by finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by it. The GCD is the largest number that divides both numbers without leaving a remainder.
To simplify 20/625, we need to find the GCD of 20 and 625. One method is to list the factors of each number:
- Factors of 20: 1, 2, 4, 5, 10, 20
- Factors of 625: 1, 5, 25, 125, 625
The largest number that appears in both lists is 5. Therefore, the GCD of 20 and 625 is 5.
Now, we divide both the numerator and the denominator by 5:
20 ÷ 5 = 4 625 ÷ 5 = 125
Therefore, the simplified form of 20/625 is 4/125. This simplified fraction is equivalent to the original fraction, meaning they represent the same value.
Exploring Equivalent Fractions: Different Representations, Same Value
A key concept in fractions is the idea of equivalent fractions. These are fractions that have different numerators and denominators but represent the same value. We can obtain equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number.
For example, if we multiply both the numerator and denominator of 4/125 by 2, we get 8/250. Both 4/125 and 8/250 are equivalent fractions. Similarly, multiplying by 3 gives us 12/375, and so on. Dividing by a common factor, as we did in the simplification process, also produces equivalent fractions.
20/625 as a Decimal and Percentage: Alternative Representations
Fractions can also be expressed as decimals and percentages. To convert 20/625 (or its simplified form, 4/125) into a decimal, we perform the division:
4 ÷ 125 = 0.032
To convert the decimal 0.032 into a percentage, we multiply by 100:
0.032 × 100 = 3.2%
Therefore, 20/625 is equivalent to 0.032 and 3.2%.
Real-World Applications of Fractions and Ratios: Beyond the Classroom
The concepts of fractions and ratios are not confined to the mathematical realm; they permeate various aspects of our daily lives. Let's consider some examples where understanding 20/625 (or its equivalent representations) could be relevant:
-
Proportions and Scaling: Imagine you're working on a model of a building. If the model's height is 20 cm and the actual building's height is 625 cm, the ratio is 20:625, which simplifies to 4:125. This ratio helps maintain accurate proportions throughout the model.
-
Financial Calculations: Percentages are frequently used in finance. If you receive a 3.2% interest rate on your savings, it directly relates to the fraction 20/625.
-
Mixing Ingredients: In cooking or crafting, understanding ratios is crucial. If a recipe calls for a specific ratio of ingredients, you can adapt the recipe by scaling up or down using the principles of equivalent fractions.
-
Data Analysis and Probability: In statistical analysis, fractions and percentages are essential for interpreting data and calculating probabilities. For instance, if 20 out of 625 participants in a survey responded positively, the fraction 20/625 represents the proportion of positive responses.
Working with Ratios: Understanding the Relationship Between Quantities
A ratio is a comparison of two or more quantities. It can be expressed in different ways: using a colon (e.g., 20:625), as a fraction (e.g., 20/625), or using the word "to" (e.g., 20 to 625). Ratios are fundamental to understanding proportions and solving problems involving scaling, mixtures, and comparisons. The ratio 20:625 simplifies to 4:125, indicating that for every 4 units of one quantity, there are 125 units of another quantity.
Advanced Concepts: Connecting Fractions to Other Mathematical Fields
The seemingly simple fraction 20/625 serves as a gateway to more complex mathematical concepts:
-
Algebra: Fractions are crucial in algebraic equations and manipulations. Solving for unknown variables often involves working with fractions and simplifying expressions.
-
Calculus: Calculus relies heavily on the understanding of limits and infinitesimals, which are closely related to the concepts of fractions and their behavior as denominators approach zero.
-
Geometry: Fractions are used in geometric calculations, such as finding the area of a triangle or the volume of a cylinder.
-
Statistics: As mentioned earlier, fractions and percentages are essential for interpreting data, calculating probabilities, and understanding statistical distributions.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 20/625?
A1: The simplest form of 20/625 is 4/125.
Q2: How do I convert 20/625 to a decimal?
A2: Divide the numerator (20) by the denominator (625): 20 ÷ 625 = 0.032
Q3: How do I convert 20/625 to a percentage?
A3: Convert the decimal equivalent (0.032) to a percentage by multiplying by 100: 0.032 × 100 = 3.2%
Q4: What are some real-world applications of this fraction?
A4: Real-world applications include scaling models, calculating percentages in finance, mixing ingredients in recipes, and analyzing data in statistics.
Q5: Can I use a calculator to simplify fractions?
A5: Yes, many calculators have functions to simplify fractions. However, understanding the underlying process of finding the GCD is crucial for developing mathematical proficiency.
Conclusion: The Significance of Simplicity in Mathematics
The exploration of 20/625, while seemingly simple, has revealed the interconnectedness of various mathematical concepts. Simplifying fractions, understanding ratios, and applying these concepts to real-world situations are essential skills for anyone seeking a strong foundation in mathematics. This journey illustrates that even the most basic mathematical entities can lead to profound insights and practical applications, highlighting the power and beauty of mathematics in everyday life. By grasping the fundamentals, we unlock the ability to tackle more complex challenges and appreciate the elegance of mathematical principles. Remember, the key is not just to find the answer, but to understand the why behind it. This understanding will serve you well in all future mathematical endeavors.
Latest Posts
Latest Posts
-
Examen In English
Sep 19, 2025
-
1 5cm In Mm
Sep 19, 2025
-
2000 X 6
Sep 19, 2025
-
Bruegel Peasant Wedding
Sep 19, 2025
-
24 9 Simplified
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 625 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.