67 X 3
interactiveleap
Sep 19, 2025 · 6 min read
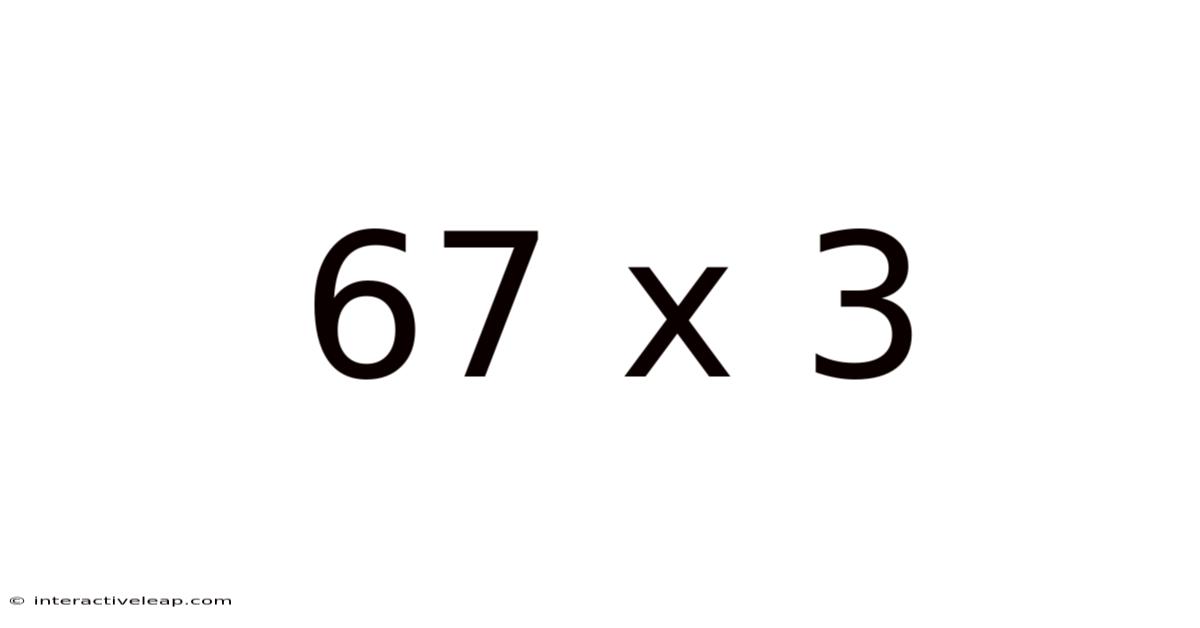
Table of Contents
Decoding 67 x 3: A Deep Dive into Multiplication and Beyond
This article explores the seemingly simple multiplication problem, 67 x 3, as a gateway to understanding fundamental mathematical concepts. We'll move beyond the basic answer to delve into the underlying principles, different methods of calculation, and the broader applications of multiplication in everyday life and advanced mathematics. This comprehensive guide is perfect for students seeking a deeper understanding, educators looking for engaging teaching materials, or anyone curious about the fascinating world of numbers.
I. Introduction: More Than Just an Answer
At first glance, 67 x 3 seems straightforward. A quick calculation yields the answer 201. However, this seemingly simple problem provides a fertile ground for exploring various mathematical concepts and techniques. We will examine different methods of solving this multiplication, including standard algorithms, mental math strategies, and visual representations. Furthermore, we'll explore the broader implications of multiplication, its relationship to other arithmetic operations, and its crucial role in various fields, from accounting to astrophysics. This exploration will reveal that 67 x 3 is much more than just a numerical result; it's a key to unlocking a deeper understanding of mathematics.
II. Standard Multiplication Algorithm: A Step-by-Step Approach
The standard algorithm for multiplication is a widely taught method that breaks down the problem into smaller, manageable steps. Let's apply it to 67 x 3:
-
Multiply the ones digit: 3 x 7 = 21. Write down the '1' and carry-over the '2'.
-
Multiply the tens digit: 3 x 6 = 18. Add the carried-over '2': 18 + 2 = 20. Write down '20'.
-
Combine the results: The final answer is 201.
This method is systematic and reliable, making it suitable for various multiplication problems, regardless of the number of digits. However, it’s crucial to understand the underlying principle: we are essentially multiplying 3 by each digit of 67 (the tens and the ones place) and then adding the results. This breakdown makes the multiplication process more manageable, even with larger numbers.
III. Mental Math Strategies: Speed and Efficiency
While the standard algorithm is reliable, mental math techniques can improve speed and calculation efficiency. Several strategies can be employed to solve 67 x 3 mentally:
-
Distributive Property: Rewrite 67 as (60 + 7). Then, apply the distributive property: 3 x (60 + 7) = (3 x 60) + (3 x 7) = 180 + 21 = 201. This method breaks down the larger multiplication into smaller, more easily manageable multiplications.
-
Rounding and Compensation: Round 67 to 70. Multiply 70 x 3 = 210. Since we rounded up by 3, subtract 3 x 3 = 9 from 210: 210 - 9 = 201. This method uses estimation to simplify the calculation and then adjusts for the rounding error.
-
Doubling and Halving: While not directly applicable in this specific instance, this strategy is effective for other multiplication problems. For example, to solve 67 x 6, you could double 67 (134) and then double it again (268), or you could solve 67 x 2 (134) and multiply by 3 which is 134 + 134 + 134 = 402. This method exploits the relationship between multiplication and doubling/halving.
IV. Visual Representations: A Concrete Approach
Visual aids can greatly enhance understanding, especially for younger learners. Several ways to visualize 67 x 3 include:
-
Repeated Addition: Draw 67 objects three times. Counting all the objects will yield the answer 201. This directly links multiplication to repeated addition, reinforcing the fundamental concept.
-
Area Model: Draw a rectangle with sides representing 60 and 7 (representing the tens and ones of 67) and a height of 3. Divide the rectangle into smaller rectangles, calculate the area of each (3 x 60 = 180 and 3 x 7 = 21), and add the areas together (180 + 21 = 201). This visual representation connects multiplication with area, providing a geometric interpretation.
V. The Broader Significance of Multiplication
Multiplication is more than a simple arithmetic operation; it’s a fundamental concept with wide-ranging applications:
-
Everyday Life: Calculating the total cost of multiple items, determining the area of a room, figuring out travel time, and numerous other daily activities rely on multiplication.
-
Science and Engineering: Multiplication is essential in physics, chemistry, and engineering for various calculations, such as determining force, calculating speed and velocity, and solving equations of motion.
-
Finance and Accounting: Multiplication is fundamental to financial calculations, such as computing interest, calculating taxes, and determining profit margins.
-
Computer Science: Multiplication is a core operation in computer programming and algorithms, powering many computational processes.
VI. Connection to Other Mathematical Concepts
Multiplication is intricately linked to other mathematical concepts:
-
Addition: Multiplication is essentially repeated addition. 67 x 3 is equivalent to 67 + 67 + 67.
-
Division: Multiplication and division are inverse operations. The result of 67 x 3 (201) can be divided by 3 to get back to 67.
-
Exponents: Multiplication forms the basis for understanding exponents. For example, 67³ (67 cubed) means 67 x 67 x 67.
-
Algebra: Multiplication is a central element in algebraic equations and expressions, where variables and numbers interact through multiplicative operations.
VII. Exploring Larger Numbers and More Complex Multiplications
The principles we've discussed for 67 x 3 are easily scalable to more complex multiplication problems. Understanding the distributive property, mental math strategies, and visual aids helps simplify multiplication of larger numbers. For example, to solve 123 x 45, you could break it down using the distributive property: (100 + 20 + 3) x (40 + 5), expanding to a series of smaller multiplications and then adding the results. Similar strategies are employed for multiplying decimals and fractions.
VIII. Frequently Asked Questions (FAQ)
-
What is the easiest way to multiply 67 x 3? The easiest way depends on individual preference and skill level. The standard algorithm is reliable, while mental math strategies (like the distributive property) can be quicker for those proficient in mental calculation.
-
How can I explain 67 x 3 to a young child? Use visual aids like counters or drawings to represent repeated addition. Draw 3 groups of 67 objects and have the child count them all.
-
Are there any tricks to multiplying larger numbers quickly? Yes, there are various mental math techniques and algorithms designed for efficient multiplication of larger numbers. These often involve breaking down the problem into smaller, simpler multiplications.
-
What if I make a mistake during multiplication? Check your work carefully, step-by-step. Use different methods (standard algorithm, mental math, visual representation) to verify the result.
IX. Conclusion: The Enduring Power of Multiplication
Solving 67 x 3, initially perceived as a simple task, opens a door to a deeper understanding of fundamental mathematical principles and their real-world applications. We’ve explored different calculation methods, highlighting the versatility and importance of multiplication across diverse fields. By mastering multiplication, we not only acquire a crucial skill but also cultivate a stronger foundation for advanced mathematical concepts. The exploration of 67 x 3 serves as a reminder that even seemingly basic mathematical problems hold significant learning potential and can provide a pathway to a richer appreciation of the beauty and power of mathematics. The journey to understand numbers is ongoing, and every problem solved, no matter how simple it might seem, contributes to that journey. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
Double Eagle Coin
Sep 19, 2025
-
4 5 X 5
Sep 19, 2025
-
20 Of 625
Sep 19, 2025
-
36 2c To F
Sep 19, 2025
-
2x 3 2
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 67 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.