25 Divided 7
interactiveleap
Sep 19, 2025 · 5 min read
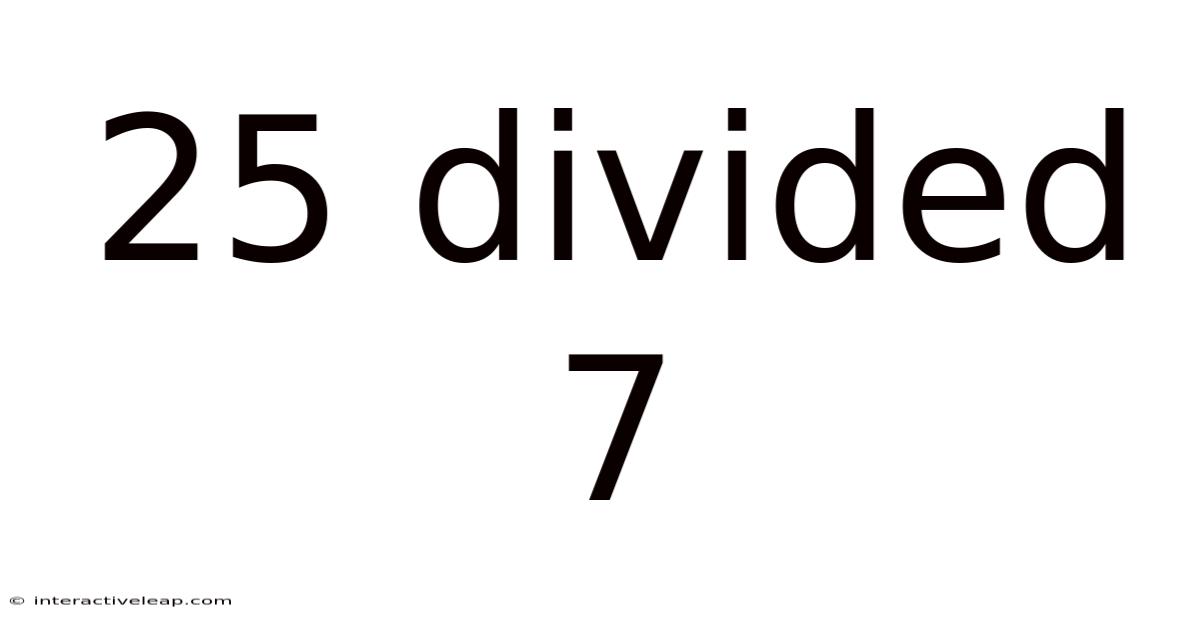
Table of Contents
Unveiling the Mystery: A Deep Dive into 25 Divided by 7
Dividing 25 by 7 might seem like a simple arithmetic problem, something you'd quickly solve on a calculator. But beneath the surface of this seemingly straightforward calculation lies a wealth of mathematical concepts that extend far beyond a simple answer. This article will explore the division of 25 by 7 in detail, examining various approaches, delving into the underlying principles, and even touching upon its relevance in broader mathematical contexts. We'll move beyond a simple quotient and remainder to understand the true meaning of this operation.
Understanding the Basics: Division and its Components
Before we dive into the specifics of 25 divided by 7, let's refresh our understanding of division. Division is essentially the inverse operation of multiplication. It involves splitting a quantity (the dividend) into equal parts (the divisor) to determine the number of parts (the quotient) and any remaining amount (the remainder). In the expression 25 ÷ 7, 25 is the dividend, 7 is the divisor, and we are looking for the quotient and the remainder.
Calculating 25 Divided by 7: The Long Division Method
The most common method for performing this calculation is long division. Let's work through it step-by-step:
-
Set up the problem: Write 7 (the divisor) outside a long division symbol and 25 (the dividend) inside.
-
Determine the quotient: How many times does 7 go into 25? 7 goes into 25 three times (7 x 3 = 21). Write the 3 above the 5 in 25.
-
Multiply and subtract: Multiply the quotient (3) by the divisor (7): 3 x 7 = 21. Subtract this result from the dividend: 25 - 21 = 4.
-
Determine the remainder: The result of the subtraction (4) is the remainder. Since 4 is smaller than the divisor (7), we have reached the end of the long division process.
Therefore, 25 divided by 7 is 3 with a remainder of 4. This can be written as: 25 ÷ 7 = 3 R 4.
Representing the Result: Fractions and Decimal Approximations
While the remainder is perfectly valid, we can also express the result as a fraction or a decimal.
-
Fraction: The remainder (4) becomes the numerator of a fraction, and the divisor (7) becomes the denominator. Thus, 25 divided by 7 can be expressed as the mixed number 3 ⁴⁄₇.
-
Decimal Approximation: To obtain a decimal approximation, we can perform long division further by adding a decimal point and zeros to the dividend. This allows us to continue the division process until we reach a desired level of accuracy or a repeating pattern emerges. Performing this extended long division yields approximately 3.571428... Notice the repeating decimal pattern.
The Significance of the Remainder: Modular Arithmetic
The remainder (4) in this division problem isn't just a leftover; it holds significant importance in modular arithmetic. Modular arithmetic, also known as clock arithmetic, deals with remainders after division. In this case, 25 ≡ 4 (mod 7), meaning that 25 and 4 are congruent modulo 7 because they have the same remainder when divided by 7. This concept is crucial in various fields like cryptography and computer science.
Exploring the Concept of Divisibility and Prime Numbers
The problem of 25 divided by 7 also touches upon the concepts of divisibility and prime numbers. A number is divisible by another if the remainder is zero when the first number is divided by the second. 7 is a prime number, meaning it is only divisible by 1 and itself. Since the remainder when 25 is divided by 7 is 4 (not 0), we can conclude that 25 is not divisible by 7.
Real-World Applications: Problem-Solving and Practical Uses
The seemingly simple division of 25 by 7 finds practical applications in numerous real-world scenarios:
-
Distribution Problems: Imagine you have 25 apples and want to distribute them equally among 7 friends. Each friend would receive 3 apples, and you would have 4 apples left over.
-
Measurement and Conversion: If you're working with measurements, you might encounter situations where you need to convert units. For example, if you have 25 inches and need to convert it to groups of 7 inches, you'd find you have 3 groups of 7 inches with 4 inches remaining.
-
Resource Allocation: In project management or resource allocation, similar scenarios arise where a total quantity needs to be divided among a certain number of units, resulting in a quotient and remainder.
Beyond the Basics: Extending the Concept
The calculation of 25 divided by 7 can be used as a springboard to explore more advanced mathematical concepts:
-
Continued Fractions: The decimal representation of 25/7 can be expressed as a continued fraction, providing an alternative way to represent the number and revealing interesting patterns.
-
Euclidean Algorithm: This algorithm utilizes repeated division to find the greatest common divisor (GCD) of two numbers. Applying the Euclidean algorithm to 25 and 7 would quickly reveal that their GCD is 1, indicating they are relatively prime (meaning they share no common factors other than 1).
-
Number Theory: The concepts of divisibility, remainders, and prime numbers are central to number theory, a branch of mathematics that explores the properties of integers.
Frequently Asked Questions (FAQs)
Q: What is the exact answer to 25 divided by 7?
A: The exact answer is 3 with a remainder of 4, which can be expressed as the mixed number 3 ⁴⁄₇ or the decimal approximation 3.571428... (the decimal part is a repeating decimal).
Q: Why is the decimal representation of 25/7 a repeating decimal?
A: Because the fraction ⁴⁄₇ cannot be expressed as a terminating decimal. When converting fractions to decimals, repeating decimals occur when the denominator contains prime factors other than 2 and 5.
Q: How can I calculate 25 divided by 7 without a calculator?
A: The most reliable method is long division, as described earlier.
Conclusion: More Than Just an Answer
The seemingly simple calculation of 25 divided by 7 opens a door to a fascinating world of mathematical concepts. From basic arithmetic to advanced number theory, this problem illustrates the interconnectedness of various mathematical principles. Understanding not just the answer (3 R 4 or 3 ⁴⁄₇) but also the underlying concepts and applications makes this problem far more enriching than a simple arithmetic exercise. It highlights the beauty and power of mathematics in its ability to describe and solve problems in diverse areas of our lives. We hope this detailed explanation has helped you appreciate the richness and depth hidden within this seemingly simple calculation.
Latest Posts
Latest Posts
-
Double Eagle Coin
Sep 19, 2025
-
4 5 X 5
Sep 19, 2025
-
20 Of 625
Sep 19, 2025
-
36 2c To F
Sep 19, 2025
-
2x 3 2
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 25 Divided 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.