4x 2 X
interactiveleap
Sep 18, 2025 · 6 min read
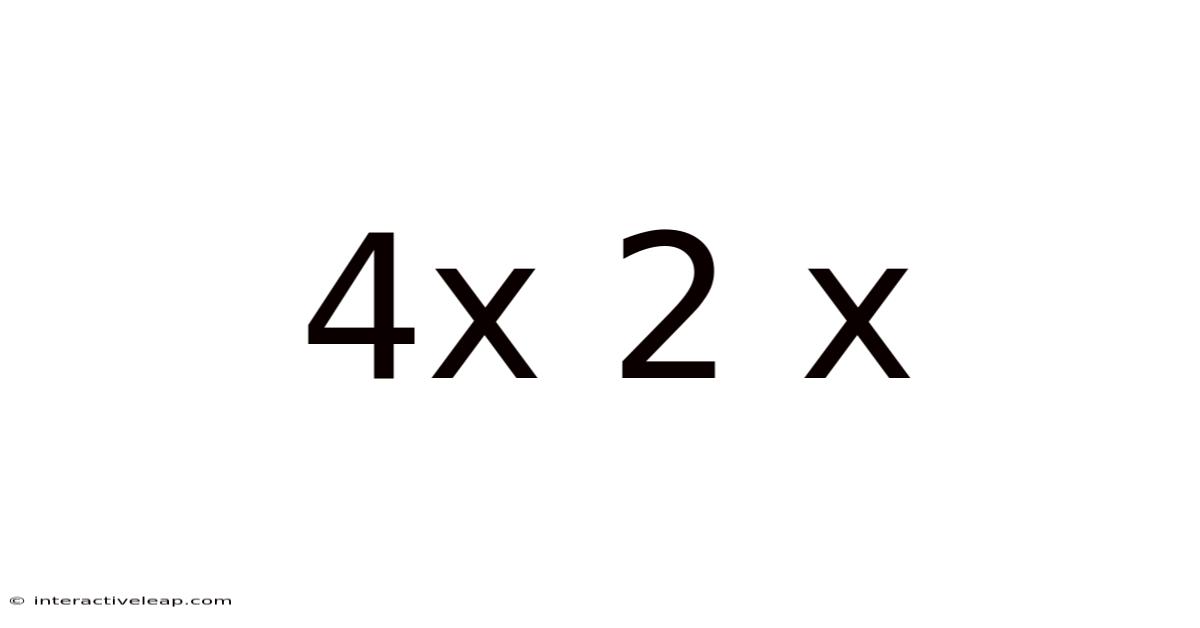
Table of Contents
Decoding 4x2x: Understanding Matrix Notation and its Applications
The notation "4x2x" might seem cryptic at first glance, but it's a concise way to represent a fundamental concept in mathematics and various fields that rely on mathematical modeling: matrices. This article will delve into the meaning of 4x2x, explore the concept of matrices in detail, and illuminate its wide-ranging applications in diverse fields, from computer graphics to quantum physics. Understanding this notation unlocks a door to a world of powerful mathematical tools.
Introduction to Matrices
A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. The "4x2x" notation refers to a three-dimensional matrix, specifying the dimensions of the matrix. The first number (4) represents the number of rows, the second (2) represents the number of columns, and the third (x) represents an unknown or variable number of "layers" or "slices." Therefore, a 4x2x matrix would have four rows and two columns, repeated 'x' times in a third dimension. While a 4x2 matrix is a flat, two-dimensional structure, adding the third dimension creates a more complex data structure.
Understanding Matrix Dimensions
The dimensions of a matrix are crucial. They determine how the matrix can be manipulated mathematically and what kind of data it can represent. Let's illustrate with simpler examples before tackling the complexities of a 4x2x matrix.
- 2x2 Matrix: This matrix has two rows and two columns. A simple example is:
[[1, 2],
[3, 4]]
- 3x2 Matrix: This matrix has three rows and two columns. An example could be:
[[1, 2],
[3, 4],
[5, 6]]
These two-dimensional matrices are relatively straightforward. Now let's move to the third dimension.
Visualizing the 4x2x Matrix
Imagine stacking multiple 4x2 matrices on top of each other. Each 4x2 matrix forms a slice or layer in the third dimension. The 'x' in "4x2x" signifies that we can have any number of these layers. If x=3, for instance, we would have three 4x2 matrices stacked together to form a 4x2x3 matrix. This concept extends to higher dimensions as well, although visualization becomes increasingly challenging beyond three dimensions.
Mathematical Operations with Matrices
Matrices are not just containers for numbers; they are mathematical objects that can be manipulated using specific operations. These operations include:
-
Addition and Subtraction: Two matrices can be added or subtracted only if they have the same dimensions. The operation is performed element-wise.
-
Scalar Multiplication: A matrix can be multiplied by a scalar (a single number). This involves multiplying each element of the matrix by the scalar.
-
Matrix Multiplication: This is more complex. The number of columns in the first matrix must equal the number of rows in the second matrix. The resulting matrix will have the number of rows of the first matrix and the number of columns of the second matrix.
-
Transpose: The transpose of a matrix is obtained by interchanging its rows and columns. The transpose of a 4x2 matrix would be a 2x4 matrix.
For a 4x2x matrix, these operations would be applied to each of the 4x2 slices individually, or in a coordinated manner depending on the specific mathematical operation.
Applications of Matrices: A Multifaceted Tool
The power of matrices lies in their ability to represent and manipulate complex data structures. Here are some key applications:
-
Computer Graphics: Matrices are fundamental to computer graphics. They are used to represent transformations such as rotations, scaling, and translations of objects in 3D space. A 4x4 matrix is commonly used to represent these transformations. The 4x2x structure could represent multiple sets of 2D transformations on a series of image slices.
-
Machine Learning and Artificial Intelligence: Matrices are central to machine learning algorithms. Data is often represented as matrices, and matrix operations are used to perform computations like finding patterns, making predictions, and training models. Consider a dataset with multiple features represented in rows and multiple data points represented in columns across different layers. The ‘x’ here could represent various datasets.
-
Quantum Mechanics: Quantum mechanics uses matrices to represent quantum states and operators. These matrices often have complex numbers as their elements, reflecting the probabilistic nature of quantum phenomena.
-
Engineering and Physics: Matrices are extensively used in structural analysis, circuit analysis, and other engineering disciplines. They are powerful tools for solving systems of linear equations. Consider representing a three-dimensional structure such as a bridge as a collection of related matrices across multiple layers.
-
Data Analysis and Statistics: Matrices are the backbone of many statistical methods. They are used to represent data sets, perform statistical calculations, and visualize data.
-
Image Processing: In image processing, a 4x2x matrix could represent various image features along the x-axis and y-axis, with each layer ('x') containing a unique set of data like pixel intensities or colour information.
-
Network Analysis: Representing connections in networks, be it social media graphs or communication networks, can use matrices. Each layer could represent a different time step or a different type of connection.
-
Cryptography: Matrix operations are employed in certain types of encryption and decryption algorithms, providing a robust security layer.
Further Exploration of Higher-Dimensional Matrices
While 4x2x represents a three-dimensional matrix, the concept extends to even higher dimensions (e.g., 4x2x3x...). These higher-dimensional matrices are less intuitive to visualize but are vital in advanced mathematical modeling and computational tasks. They are increasingly relevant in areas such as tensor analysis, big data processing, and deep learning.
Frequently Asked Questions (FAQ)
-
Q: What if 'x' is 0 in 4x2x?
- A: A 4x2x0 matrix would be an empty matrix, essentially containing no data.
-
Q: Can I use different data types within a single matrix?
- A: While a matrix is typically defined with a single data type (e.g., all integers or all floating-point numbers), some programming languages and software packages allow for more flexible data structures that might handle mixed types. However, for standard mathematical operations, consistency is crucial.
-
Q: How are 4x2x matrices stored and processed in computers?
- A: Computers generally store matrices in a linear format, often in row-major or column-major order. Efficient algorithms are used to manage and process these matrices, particularly for large-scale applications.
-
Q: What software packages are commonly used for matrix calculations?
- A: Several software packages are well-suited for handling matrix operations, including MATLAB, Python's NumPy library, R, and specialized linear algebra libraries.
Conclusion
The notation "4x2x" encapsulates a powerful and versatile mathematical tool: the three-dimensional matrix. While seemingly simple, this representation unlocks a broad spectrum of applications in various fields. Understanding matrix notation and operations is essential for anyone working in areas that involve data processing, modeling, or any domain leveraging linear algebra. From computer graphics to quantum physics, the versatility and power of matrices continue to drive innovation and advancements across diverse scientific and technological domains. Further exploration of matrix algebra will reveal its immense capability and its crucial role in shaping modern technology and scientific understanding. This foundational knowledge empowers us to understand and contribute to the increasingly complex mathematical landscape of our world.
Latest Posts
Latest Posts
-
70 Of 170
Sep 19, 2025
-
60 Of 1200
Sep 19, 2025
-
30 Of 450
Sep 19, 2025
-
15 Off 42
Sep 19, 2025
-
Best Plyometric Workouts
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 4x 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.