3/4 Of 40
interactiveleap
Sep 18, 2025 · 6 min read
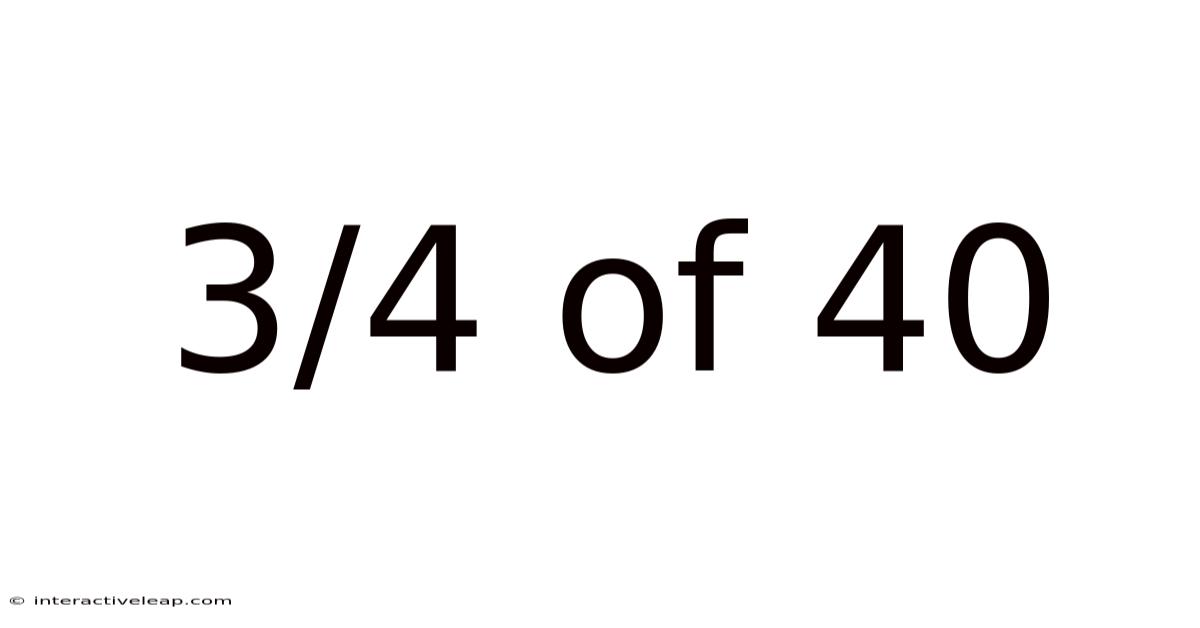
Table of Contents
Decoding 3/4 of 40: A Comprehensive Guide to Fractions and Their Applications
Finding 3/4 of 40 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation unlocks a deeper understanding of fractions, their applications in everyday life, and their importance in more advanced mathematical concepts. This article will delve into the solution, exploring the underlying principles of fractions, providing multiple methods for solving the problem, and showcasing the broader relevance of fractional calculations.
Understanding Fractions: A Foundation
Before we tackle 3/4 of 40, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we're dealing with three out of four equal parts.
Fractions can be represented visually, using diagrams like pie charts or bar models. This visual representation is particularly helpful for grasping the concept, especially for beginners. Imagine a pizza cut into four equal slices. 3/4 of the pizza represents three of those four slices.
Method 1: Direct Calculation (Multiplication)
The most straightforward way to calculate 3/4 of 40 is through direct multiplication. We can rewrite "of" as multiplication. Therefore, 3/4 of 40 is equivalent to (3/4) * 40.
To perform this calculation:
- Multiply the numerator by the whole number: 3 * 40 = 120
- Divide the result by the denominator: 120 / 4 = 30
Therefore, 3/4 of 40 is 30.
Method 2: Finding the Unit Fraction (1/4)
This method is particularly useful for visualizing the problem and strengthening the understanding of fractions. We first find the value of one-quarter (1/4) of 40.
- Divide the whole number by the denominator: 40 / 4 = 10. This means 1/4 of 40 is 10.
- Multiply the unit fraction value by the numerator: 10 * 3 = 30
This again confirms that 3/4 of 40 is 30.
Method 3: Converting the Fraction to a Decimal
Another approach involves converting the fraction 3/4 into its decimal equivalent.
- Divide the numerator by the denominator: 3 / 4 = 0.75
- Multiply the decimal by the whole number: 0.75 * 40 = 30
This method highlights the interchangeable nature of fractions and decimals, demonstrating that they represent the same proportional value.
Real-World Applications of Fractional Calculations
The seemingly simple calculation of 3/4 of 40 has widespread applications in various real-world scenarios:
- Shopping: Calculating discounts. If an item is 25% (which is equivalent to 1/4) off, and the original price is 40, finding 1/4 of 40 helps determine the discount amount.
- Cooking: Scaling recipes. If a recipe calls for 40 grams of flour and you want to make 3/4 of the recipe, this calculation helps determine the required amount of flour.
- Construction and Engineering: Measuring materials. Calculating the length of materials needed for a project often involves fractions. For example, if a project requires 40 meters of wire, and you only need 3/4 of that length, this calculation is essential.
- Finance: Calculating interest or shares. Understanding fractions is crucial in managing personal finance, calculating portions of investments, and understanding interest rates.
- Data Analysis: Representing proportions. Fractions are frequently used to represent proportions in data analysis and statistics. For example, if a survey of 40 people shows that 30 prefer a particular brand, this can be expressed as 3/4.
Extending the Concept: Working with More Complex Fractions
While 3/4 of 40 is a relatively straightforward calculation, the principles involved extend to more complex fractions and whole numbers. The core concept remains the same: multiplication and division.
For example, let's consider finding 5/8 of 64:
- Multiply the numerator by the whole number: 5 * 64 = 320
- Divide the result by the denominator: 320 / 8 = 40
Therefore, 5/8 of 64 is 40.
Alternatively, we can first find 1/8 of 64 (64/8 = 8) and then multiply by 5 (8 * 5 = 40).
Dealing with Improper Fractions and Mixed Numbers
The concepts extend to improper fractions (where the numerator is larger than the denominator) and mixed numbers (a combination of a whole number and a fraction). For example, let's consider 7/4 of 40:
- Multiply the numerator by the whole number: 7 * 40 = 280
- Divide the result by the denominator: 280 / 4 = 70
Alternatively, we can convert the improper fraction 7/4 to a mixed number (1 ¾). This would mean calculating 1 whole of 40 (which is 40) plus ¾ of 40 (which, as we've already established, is 30), resulting in 70.
This illustrates that understanding the relationship between improper fractions, mixed numbers, and their decimal equivalents is crucial for efficient calculations.
Frequently Asked Questions (FAQs)
-
Q: What if the whole number is not easily divisible by the denominator?
A: You can still use the multiplication method: multiply the numerator and the whole number, then divide by the denominator. You might end up with a fraction or a decimal as a result.
-
Q: Are there any shortcuts for specific fractions?
A: Yes, understanding the relationship between fractions and percentages can be helpful. For example, 1/4 is equivalent to 25%, 1/2 is 50%, and 3/4 is 75%. This can sometimes simplify the calculation, particularly with common fractions.
-
Q: How can I improve my understanding of fractions?
A: Practice is key! Start with simple problems and gradually increase the complexity. Use visual aids like diagrams and manipulatives. And, most importantly, focus on understanding the underlying concepts rather than just memorizing formulas.
Conclusion: Mastering Fractions - A Stepping Stone to Further Mathematical Understanding
The seemingly simple problem of finding 3/4 of 40 provides a gateway to a deeper understanding of fractions and their importance in mathematics and everyday life. From calculating discounts and scaling recipes to understanding more complex mathematical concepts, mastering fractions is a crucial skill. By understanding different calculation methods and exploring real-world applications, we can build a strong foundation in this fundamental aspect of mathematics, paving the way for success in more advanced mathematical studies and problem-solving in various fields. Remember, the key is not just to get the right answer (30), but to understand why and how you arrived at that answer. This understanding will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
Oz In Teaspoon
Sep 18, 2025
-
Factorise 12x 8
Sep 18, 2025
-
100 X 2
Sep 18, 2025
-
77f To C
Sep 18, 2025
-
5 0 X 10
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.