100 X 2
interactiveleap
Sep 18, 2025 · 6 min read
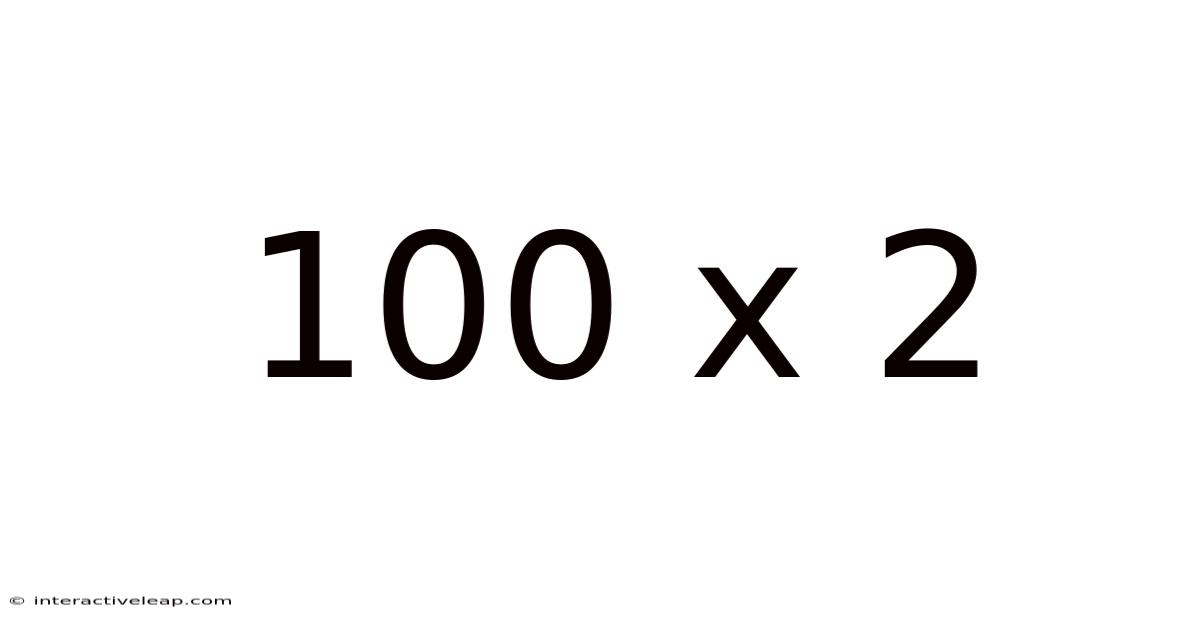
Table of Contents
Decoding 100 x 2: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple equation, 100 x 2, delving far beyond the immediate answer of 200. We'll examine the fundamental mathematical principles involved, explore its real-world applications across various fields, and uncover the fascinating connections to broader mathematical concepts. Understanding this basic multiplication problem unlocks a gateway to more complex mathematical operations and their significance in our daily lives.
Understanding the Fundamentals: Multiplication as Repeated Addition
At its core, multiplication is a shortcut for repeated addition. The equation 100 x 2 simply means adding 100 to itself two times: 100 + 100 = 200. This foundational understanding is crucial, especially for grasping the concept in younger learners. Visual aids like counters or blocks can effectively demonstrate this principle, making abstract concepts more concrete and easier to grasp. This method of representing multiplication as repeated addition helps build a strong foundation for more complex mathematical operations in the future.
The Commutative Property: Order Doesn't Matter
Multiplication possesses a valuable property known as the commutative property. This means that the order of the numbers being multiplied doesn't affect the result. In this case, 100 x 2 is identical to 2 x 100. Both expressions will always equal 200. This seemingly minor detail holds significant implications in simplifying calculations and problem-solving across various mathematical contexts. Understanding the commutative property allows for flexibility and efficiency in performing multiplications, especially with larger numbers.
Beyond the Basics: Exploring Different Methods of Multiplication
While the repeated addition method is excellent for beginners, other techniques can efficiently solve 100 x 2 and more complex multiplications.
-
Using Place Value: Understanding place value is essential for efficient multiplication. The number 100 represents 1 hundred, 0 tens, and 0 ones. Multiplying this by 2 means doubling each place value: 2 hundreds, 0 tens, and 0 ones, resulting in 200. This method highlights the structure of numbers and the importance of place value in mathematical operations.
-
Distributive Property: The distributive property allows us to break down complex multiplications into simpler ones. While not strictly necessary for 100 x 2, it's valuable for understanding more advanced calculations. For instance, if we were multiplying 102 x 2, we could use the distributive property: (100 x 2) + (2 x 2) = 200 + 4 = 204. This approach simplifies more complicated multiplications by breaking them into manageable parts.
-
Mental Math Techniques: With practice, we can develop mental math strategies for quick calculations. For 100 x 2, visualizing two hundreds immediately yields the answer 200. These mental math skills are highly beneficial in everyday situations, improving calculation speed and accuracy.
Real-World Applications: Where 100 x 2 Shows Up
The seemingly simple equation 100 x 2 appears in numerous everyday scenarios:
-
Shopping: Imagine buying two items costing $100 each. The total cost is 100 x 2 = $200. This basic calculation is essential for managing personal finances.
-
Measurement: If you have two lengths of 100 centimeters each, the combined length is 100 x 2 = 200 centimeters or 2 meters. Understanding multiplication is critical for tasks involving measurement and conversion.
-
Cooking: If a recipe calls for 100 grams of flour per serving and you want to make two servings, you'll need 100 x 2 = 200 grams of flour. Multiplication is frequently used in cooking and baking to scale recipes.
-
Engineering and Construction: In many engineering projects, multiplication is essential for calculating areas, volumes, and materials needed. A simple calculation of 100 x 2 might represent the number of components needed or the distance between two points.
-
Data Analysis: In data analysis and statistics, the multiplication of values is a frequent operation in various calculations, including finding averages, percentages, and proportions. Even a seemingly simple operation like 100 x 2 might represent a crucial calculation within a larger dataset.
Connecting to Larger Concepts: Scaling and Proportionality
Understanding 100 x 2 is a stepping stone to comprehending larger concepts like scaling and proportionality. Scaling involves increasing or decreasing the size of something proportionally. If a map has a scale of 1:100, then 2 centimeters on the map represent 2 x 100 = 200 centimeters or 2 meters in reality. Proportionality is the relationship between two quantities where their ratio remains constant. This concept is fundamental in various fields, including physics, engineering, and economics.
Exploring Higher-Level Mathematics: Extensions and Applications
The seemingly simple operation 100 x 2 can be extended to explore more advanced mathematical concepts:
-
Algebra: The equation can be generalized in algebra as ax = b, where 'a' and 'b' are variables. Solving for x demonstrates a fundamental algebraic concept—finding an unknown value. In our example, 100x = 200, solving for x leads us back to x = 2.
-
Calculus: While not directly applicable, the concept of multiplication forms the basis for understanding derivatives and integrals in calculus. These operations are fundamental to understanding rates of change and accumulation, critical in physics, engineering, and economics.
-
Linear Algebra: The equation can be represented as a simple matrix multiplication, illustrating the connection between scalar multiplication and matrix algebra.
-
Number Theory: Analyzing the factors of 200 (the result of 100 x 2) provides insights into number theory, which studies the properties of integers. The prime factorization of 200 (2³ x 5²) reveals its fundamental building blocks.
Frequently Asked Questions (FAQ)
-
Q: What is the quickest way to calculate 100 x 2?
- A: The quickest way is to recognize that multiplying by 2 is simply doubling. Therefore, doubling 100 gives you 200.
-
Q: Is there a difference between 100 x 2 and 2 x 100?
- A: No, due to the commutative property of multiplication, both expressions result in the same answer: 200.
-
Q: How can I explain 100 x 2 to a young child?
- A: Use visual aids like counters or blocks. Show them 100 counters, then add another 100 counters. Count them all together to show that 100 + 100 = 200.
-
Q: Are there any real-world examples beyond those mentioned?
- A: Yes, numerous everyday situations utilize this multiplication. Consider calculating the total cost of two identical items, determining the total distance traveled by covering the same distance twice, or doubling a recipe. The applications are vast and diverse.
Conclusion: The Significance of Simplicity
The equation 100 x 2, while seemingly trivial, serves as a potent example of the fundamental building blocks of mathematics. Its simplicity belies its importance, providing a stepping stone to more advanced mathematical concepts and practical applications across a multitude of fields. Understanding this basic operation is crucial for developing a solid mathematical foundation and enhancing problem-solving skills in various aspects of life. The exploration of this seemingly basic equation reveals the intricate and interconnected nature of mathematics, highlighting the power and beauty hidden within even the simplest of calculations. Mastering this fundamental concept opens doors to a deeper understanding of the world around us and the mathematical principles that govern it.
Latest Posts
Latest Posts
-
42 In Binary
Sep 18, 2025
-
4x5 In Pixels
Sep 18, 2025
-
25 Of 8
Sep 18, 2025
-
75 Of 36
Sep 18, 2025
-
3000g To Lbs
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 100 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.