25 Of 120
interactiveleap
Sep 16, 2025 · 5 min read
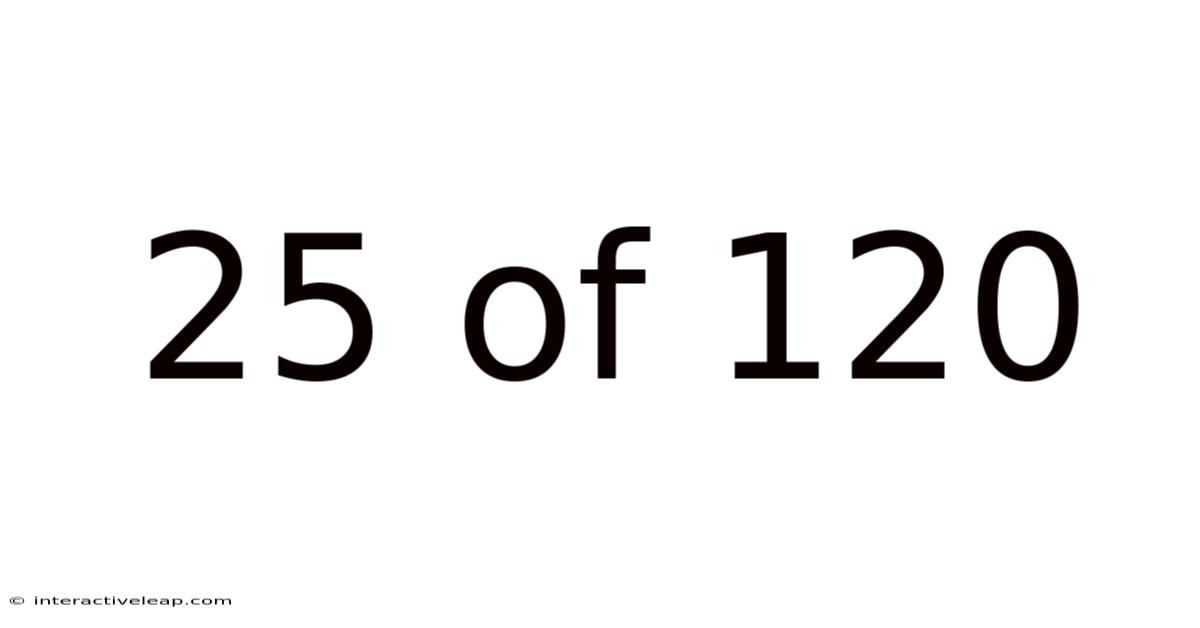
Table of Contents
Unveiling the Mystery: Understanding the Fraction 25/120 and its Implications
The seemingly simple fraction 25/120 might appear insignificant at first glance. However, understanding its simplification, applications, and the broader mathematical concepts it represents unlocks a deeper appreciation for the world of numbers. This article delves into the intricacies of 25/120, exploring its reduction to its simplest form, demonstrating practical applications, and explaining the underlying mathematical principles. We will also address frequently asked questions and provide concluding thoughts to solidify your understanding.
Introduction: Decoding 25/120
The fraction 25/120 represents a part-to-whole relationship. It signifies 25 units out of a total of 120 units. While this representation is accurate, it's not the most efficient or easily understood form. The key to unlocking its true meaning lies in simplifying the fraction to its lowest terms. This process involves finding the greatest common divisor (GCD) of both the numerator (25) and the denominator (120) and dividing both by that number. This will reveal the fraction's essence and make it easier to use in various mathematical operations and real-world scenarios. Understanding this simple fraction opens the door to comprehending more complex fractions and ratios, laying a crucial foundation for advanced mathematical concepts.
Simplifying 25/120 to its Lowest Terms
To simplify 25/120, we need to find the greatest common divisor (GCD) of 25 and 120. The GCD is the largest number that divides both 25 and 120 without leaving a remainder. One method to find the GCD is through prime factorization.
- Prime Factorization of 25: 5 x 5 = 5²
- Prime Factorization of 120: 2 x 2 x 2 x 3 x 5 = 2³ x 3 x 5
By comparing the prime factorizations, we identify the common factor: 5. Therefore, the GCD of 25 and 120 is 5.
Now, we divide both the numerator and the denominator by the GCD:
25 ÷ 5 = 5 120 ÷ 5 = 24
Therefore, the simplified form of 25/120 is 5/24. This simplified fraction is equivalent to the original fraction but is much easier to work with. It provides a clearer representation of the relationship between the parts and the whole.
Practical Applications of 25/120 (and 5/24)
The fraction 25/120, or its simplified form 5/24, has numerous real-world applications. Let's explore a few examples:
-
Calculating Percentages: To express 25/120 as a percentage, we can first simplify it to 5/24 and then divide the numerator by the denominator: 5 ÷ 24 ≈ 0.2083. Multiplying by 100 gives us approximately 20.83%. This could represent, for instance, the percentage of students who passed a test, the percentage of a task completed, or the percentage of a product sold.
-
Proportions and Ratios: Fractions are essential for understanding proportions and ratios. For example, if a recipe calls for 25 grams of sugar out of a total of 120 grams of ingredients, the ratio of sugar to total ingredients is 25/120, or 5/24. This simplified ratio can be used to scale the recipe up or down proportionally. If you wanted to double the recipe, you'd use 10 grams of sugar (5 x 2) out of 48 grams (24 x 2) of total ingredients.
-
Probability: In probability, fractions represent the likelihood of an event occurring. If there are 120 equally likely outcomes, and 25 of them represent a specific event, then the probability of that event occurring is 25/120, or 5/24. This can be expressed as a decimal (approximately 0.2083) or a percentage (approximately 20.83%).
Understanding the Mathematical Principles
The simplification of fractions like 25/120 relies on several core mathematical principles:
-
Greatest Common Divisor (GCD): As discussed earlier, the GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Finding the GCD is crucial for simplifying fractions to their lowest terms. Algorithms like the Euclidean algorithm can efficiently calculate the GCD for larger numbers.
-
Equivalent Fractions: Simplifying a fraction doesn't change its value; it only changes its representation. 25/120 and 5/24 are equivalent fractions because they represent the same proportion or ratio.
-
Prime Factorization: Breaking down numbers into their prime factors (numbers divisible only by 1 and themselves) is a powerful tool for finding the GCD and understanding the fundamental building blocks of numbers.
-
Ratio and Proportion: Fractions are fundamentally expressions of ratios and proportions. They represent the relationship between two quantities, showing how one relates to the other.
Converting Fractions to Decimals and Percentages
Converting fractions to decimals and percentages is a common practice. To convert 5/24 to a decimal, simply divide the numerator (5) by the denominator (24): 5 ÷ 24 ≈ 0.2083. To express this as a percentage, multiply the decimal by 100: 0.2083 x 100 ≈ 20.83%.
Further Exploration: Working with More Complex Fractions
The principles applied to simplifying 25/120 can be extended to more complex fractions. The key is always to find the GCD of the numerator and denominator and divide both by that number. For fractions with larger numbers, using the Euclidean algorithm or prime factorization becomes particularly helpful.
Frequently Asked Questions (FAQ)
-
Q: Why is simplifying fractions important?
-
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It provides a more concise and efficient representation of the ratio or proportion.
-
Q: What if the numerator and denominator have no common factors other than 1?
-
A: If the GCD is 1, the fraction is already in its simplest form. It cannot be further simplified.
-
Q: Are there different methods for finding the GCD?
-
A: Yes, besides prime factorization, the Euclidean algorithm is a highly efficient method for finding the GCD, especially for larger numbers.
Conclusion: The Significance of 25/120
While initially appearing insignificant, the fraction 25/120, and its simplified form 5/24, offers a valuable lesson in the fundamental principles of mathematics. Understanding how to simplify fractions, apply them to real-world problems, and grasp the underlying concepts of GCD, equivalent fractions, ratios, and proportions are essential skills that extend far beyond basic arithmetic. This seemingly simple fraction serves as a gateway to a deeper understanding of numerical relationships and their applications across various fields. Mastering these fundamental concepts lays a strong foundation for more advanced mathematical studies and problem-solving. The seemingly simple act of simplifying 25/120 to 5/24 reveals a world of mathematical richness and practical utility.
Latest Posts
Latest Posts
-
0 02 To Fraction
Sep 16, 2025
-
Microgram To Gram
Sep 16, 2025
-
Jealous Opposite Word
Sep 16, 2025
-
20 Of 18 00
Sep 16, 2025
-
7 15 X 360
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.