0.02 To Fraction
interactiveleap
Sep 16, 2025 · 5 min read
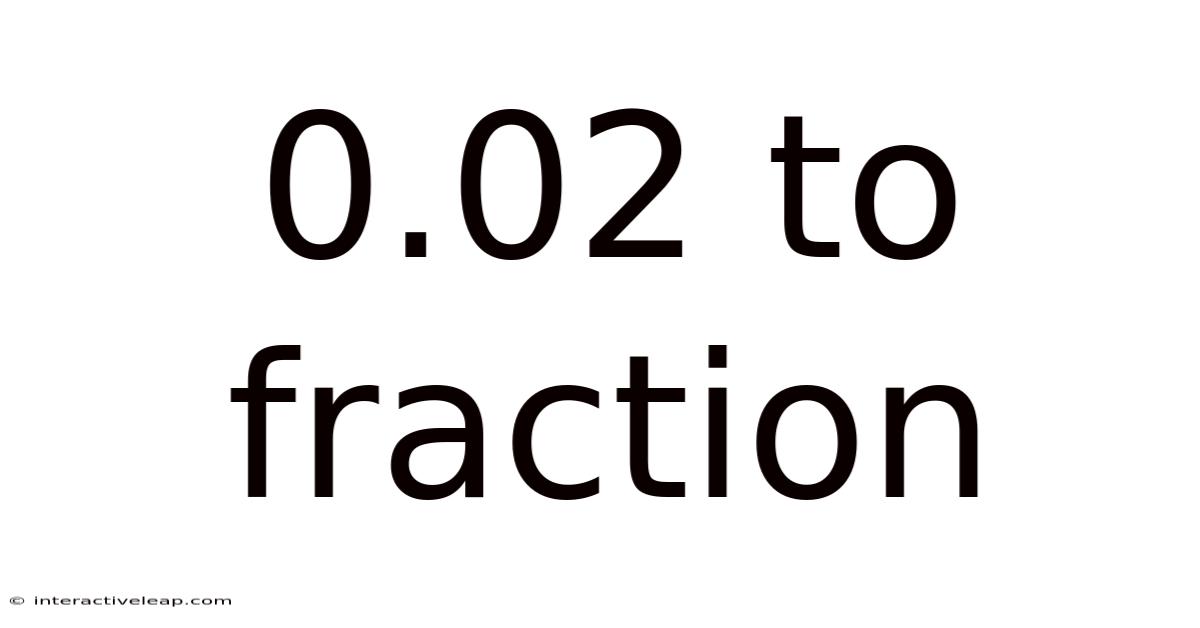
Table of Contents
From Decimal to Fraction: Mastering the Conversion of 0.02
Converting decimals to fractions might seem daunting at first, but it's a fundamental skill with wide applications in mathematics, science, and everyday life. This comprehensive guide will walk you through the process of converting the decimal 0.02 into a fraction, explaining the underlying principles and offering practical examples to solidify your understanding. We’ll explore different methods, address common misconceptions, and provide you with the tools to confidently tackle similar conversions. By the end, you'll not only know the fractional equivalent of 0.02 but also understand the broader concept of decimal-to-fraction conversion.
Understanding Decimals and Fractions
Before diving into the conversion, let's refresh our understanding of decimals and fractions. A decimal is a number that uses a decimal point to separate the whole number part from the fractional part. For example, in the decimal 0.02, the '0' to the left of the decimal point represents the whole number (zero in this case), and '02' to the right represents the fractional part.
A fraction, on the other hand, represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For instance, 1/2 (one-half) means one part out of two equal parts.
Converting 0.02 to a Fraction: A Step-by-Step Guide
The conversion of 0.02 to a fraction involves a straightforward process:
Step 1: Write the decimal as a fraction with a denominator of 1.
This is the crucial first step. We write 0.02 as a fraction over 1:
0.02/1
Step 2: Multiply both the numerator and the denominator by a power of 10 to remove the decimal point.
The number of zeros in the power of 10 should equal the number of digits after the decimal point. In 0.02, there are two digits after the decimal point, so we multiply by 10<sup>2</sup>, which is 100:
(0.02 x 100) / (1 x 100) = 2/100
Step 3: Simplify the fraction (if possible).
Now we simplify the fraction 2/100 by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 2 and 100 is 2. We divide both the numerator and the denominator by 2:
2 ÷ 2 / 100 ÷ 2 = 1/50
Therefore, the fraction equivalent of 0.02 is 1/50.
Understanding the Underlying Principles
The method described above relies on the fundamental principle that multiplying both the numerator and the denominator of a fraction by the same number (other than zero) does not change the value of the fraction. This is because we are essentially multiplying the fraction by 1 (since 100/100 = 1). Multiplying by a power of 10 effectively shifts the decimal point to the right, removing it completely and converting the decimal into a whole number in the numerator.
Alternative Methods for Decimal to Fraction Conversion
While the above method is the most straightforward, other approaches can be used, particularly for more complex decimals.
-
Using Place Value: Consider the place value of each digit after the decimal point. In 0.02, the '2' is in the hundredths place. This directly translates to a denominator of 100, giving us 2/100, which simplifies to 1/50. This method is quicker for simple decimals but less intuitive for more complex ones.
-
Converting to a Percentage then a Fraction: Decimals can easily be converted to percentages (multiply by 100). 0.02 becomes 2%. Percentages are easily converted to fractions. 2% means 2/100, which simplifies to 1/50. This method is useful for understanding the relationship between decimals, percentages, and fractions.
Further Examples and Practice
Let's practice with some more examples to solidify your understanding:
- 0.5: 0.5/1 x 10/10 = 5/10 = 1/2
- 0.75: 0.75/1 x 100/100 = 75/100 = 3/4
- 0.125: 0.125/1 x 1000/1000 = 125/1000 = 1/8
- 0.666... (recurring decimal): Recurring decimals require a slightly different approach, often involving algebraic manipulation to solve for the fraction. This is beyond the scope of this basic introduction but is a valuable topic to explore further.
Practicing these examples will help you become comfortable with the conversion process and build confidence in your abilities.
Frequently Asked Questions (FAQ)
Q1: What if the decimal has a whole number part?
A: If the decimal has a whole number part, treat the whole number separately. For example, to convert 2.02 to a fraction, first consider the whole number '2'. Then convert the decimal part '0.02' to a fraction as explained above (1/50). Finally, add the whole number and the fraction: 2 + 1/50 = 101/50 (improper fraction) or 2 1/50 (mixed number).
Q2: Can I use a calculator to convert decimals to fractions?
A: Many calculators have a function to convert decimals to fractions. This can be a helpful tool for checking your work, but understanding the underlying principles is crucial for solving problems without calculator assistance.
Q3: Why is simplifying fractions important?
A: Simplifying fractions reduces the fraction to its lowest terms, making it easier to understand and work with. It's the most concise representation of the fraction's value.
Q4: What are mixed numbers and improper fractions?
A: A mixed number is a combination of a whole number and a fraction (e.g., 2 1/50). An improper fraction has a numerator larger than its denominator (e.g., 101/50). Both represent the same value, but improper fractions are often preferred in calculations.
Conclusion
Converting decimals to fractions is a fundamental mathematical skill. The process, while seemingly simple for decimals like 0.02, forms the groundwork for understanding more complex decimal-fraction relationships. Mastering this skill will not only improve your mathematical abilities but also enhance your problem-solving skills across various disciplines. By following the steps outlined above and practicing with different examples, you’ll gain confidence and fluency in converting decimals to fractions and further your understanding of mathematical concepts. Remember, consistent practice is key to mastering this important skill.
Latest Posts
Latest Posts
-
Lacey Name Meaning
Sep 16, 2025
-
1 5 Of 35
Sep 16, 2025
-
Simplify 18 30
Sep 16, 2025
-
108 360 X 140
Sep 16, 2025
-
Radar Excel Chart
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 0.02 To Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.