Simplify 18 30
interactiveleap
Sep 16, 2025 · 6 min read
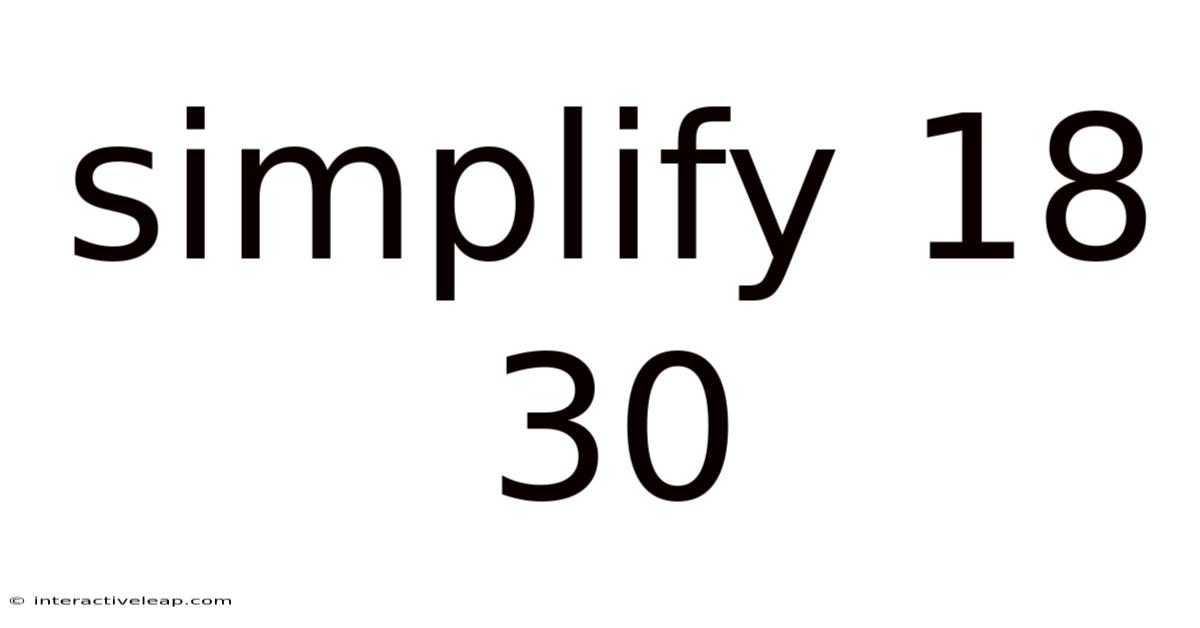
Table of Contents
Simplifying Fractions: A Deep Dive into 18/30
Understanding how to simplify fractions is a fundamental skill in mathematics. It's the cornerstone of many more advanced concepts, and mastering it builds a strong foundation for future learning. This article will delve into the process of simplifying the fraction 18/30, explaining the steps involved, the underlying mathematical principles, and offering helpful tips for simplifying other fractions. We'll explore various methods, ensuring you gain a comprehensive understanding of this essential mathematical operation. We will also address common questions and misconceptions. By the end, you’ll not only know how to simplify 18/30, but you'll be confident in your ability to simplify any fraction.
Understanding Fractions
Before we jump into simplifying 18/30, let's briefly review what a fraction represents. A fraction is a way of expressing a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. For example, in the fraction 18/30, 18 represents the number of parts we have, and 30 represents the total number of equal parts the whole is divided into.
Simplifying 18/30: The Fundamental Approach
Simplifying a fraction means reducing it to its lowest terms. This means finding an equivalent fraction where the numerator and the denominator have no common factors other than 1. This process is also known as reducing a fraction. The key to simplifying fractions lies in finding the greatest common divisor (GCD), also known as the greatest common factor (GCF), of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
To simplify 18/30, we need to find the GCD of 18 and 30. One method is to list the factors of each number:
- Factors of 18: 1, 2, 3, 6, 9, 18
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
The common factors are 1, 2, 3, and 6. The greatest common factor is 6.
Now, we divide both the numerator and the denominator by the GCD:
18 ÷ 6 = 3 30 ÷ 6 = 5
Therefore, the simplified fraction is 3/5. This means that 18/30 and 3/5 represent the same portion of a whole.
Alternative Methods for Finding the GCD
While listing factors works well for smaller numbers, it can become cumbersome with larger numbers. Here are two more efficient methods for finding the GCD:
-
Prime Factorization: This method involves breaking down each number into its prime factors. Prime factors are numbers divisible only by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 18: 2 x 3 x 3 = 2 x 3²
- Prime factorization of 30: 2 x 3 x 5
The common prime factors are 2 and 3. Multiplying these together gives us the GCD: 2 x 3 = 6. We then divide the numerator and denominator by 6, as before, to get 3/5.
-
Euclidean Algorithm: This is a more sophisticated method, particularly useful for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide the larger number (30) by the smaller number (18): 30 ÷ 18 = 1 with a remainder of 12.
- Replace the larger number with the smaller number (18) and the smaller number with the remainder (12): 18 ÷ 12 = 1 with a remainder of 6.
- Repeat: 12 ÷ 6 = 2 with a remainder of 0.
The last non-zero remainder is 6, which is the GCD. Again, we divide the numerator and denominator by 6 to get 3/5.
Visual Representation
It's often helpful to visualize fraction simplification. Imagine you have 18 slices of pizza out of a total of 30 slices. You can group these slices into sets of 6. You'll have 3 groups of 6 slices out of a total of 5 groups of 6 slices. This visually represents the simplification of 18/30 to 3/5.
Simplifying Fractions: General Strategies
The process we used for 18/30 applies to any fraction. Here's a summary of the steps:
-
Find the GCD (or GCF) of the numerator and denominator. Use any of the methods discussed above (listing factors, prime factorization, or the Euclidean algorithm).
-
Divide both the numerator and the denominator by the GCD. This will result in an equivalent fraction in its simplest form.
-
Check your answer. Make sure the resulting numerator and denominator have no common factors other than 1.
Common Mistakes and How to Avoid Them
-
Not finding the greatest common divisor: Dividing by a common factor that is not the greatest will leave the fraction partially simplified, not fully reduced. Always strive to find the GCD.
-
Incorrectly applying the division: Ensure you divide both the numerator and the denominator by the GCD. Dividing only one will change the value of the fraction.
-
Forgetting to check your answer: After simplification, double-check that the numerator and denominator share no common factors.
Frequently Asked Questions (FAQ)
Q: What if the numerator is 1? Does the fraction need simplifying?
A: If the numerator is 1, the fraction is already in its simplest form. It cannot be simplified further.
Q: What if the numerator and denominator are the same?
A: If the numerator and denominator are the same, the fraction simplifies to 1.
Q: Can I simplify a fraction by dividing the numerator and denominator by different numbers?
A: No, this will change the value of the fraction. You must divide both the numerator and the denominator by the same number (the GCD).
Q: Are there any shortcuts for simplifying fractions?
A: For simple fractions, you might be able to spot common factors quickly. However, for larger numbers, using the methods described (prime factorization or the Euclidean algorithm) is more reliable and efficient.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with. It's crucial for performing calculations and comparing fractions. In higher-level mathematics, working with simplified fractions is often essential for efficiency and accuracy.
Conclusion
Simplifying fractions is a fundamental skill that builds a strong foundation in mathematics. While the concept is simple, mastering the process requires understanding the underlying principles and employing efficient methods for finding the greatest common divisor. Whether you use factor listing, prime factorization, or the Euclidean algorithm, the goal remains the same: to reduce the fraction to its lowest terms, ensuring that the numerator and denominator share no common factors other than 1. By practicing these techniques, you'll develop fluency and confidence in handling fractions, making your journey through mathematics smoother and more rewarding. Remember, the key is to be systematic and always double-check your work!
Latest Posts
Latest Posts
-
140km In Mph
Sep 16, 2025
-
156lbs In Kg
Sep 16, 2025
-
86 To C
Sep 16, 2025
-
Mgs Magnesium Sulfide
Sep 16, 2025
-
X 3x X
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Simplify 18 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.