X 3x X
interactiveleap
Sep 16, 2025 · 7 min read
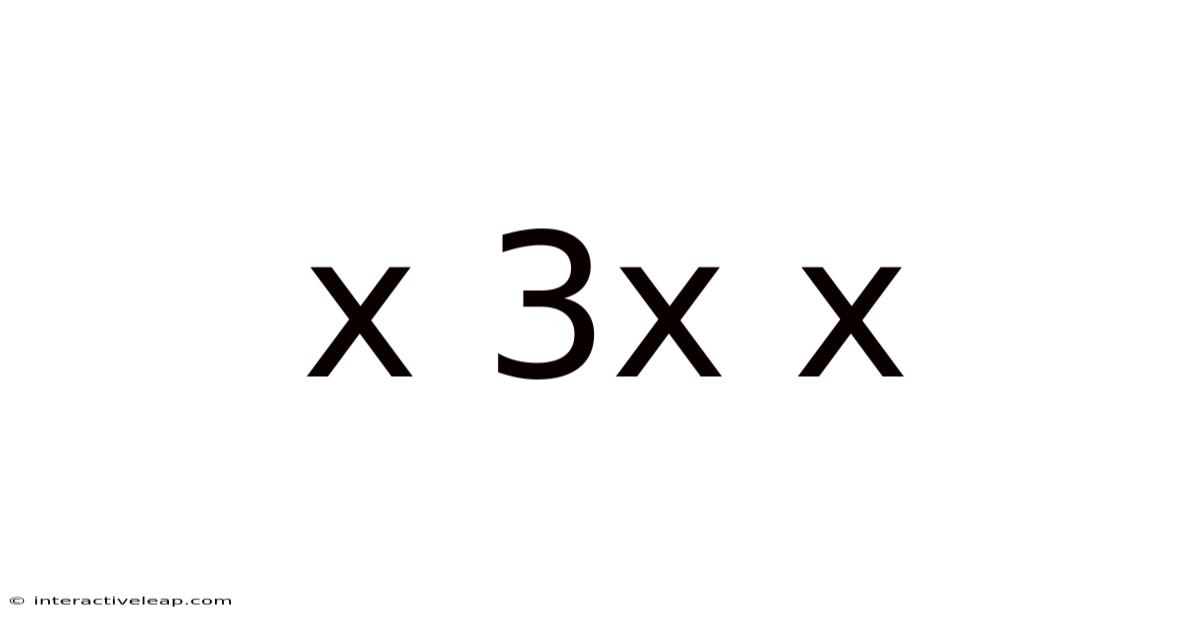
Table of Contents
Decoding the Mystery: Exploring the Pattern of x, 3x, x
The seemingly simple sequence "x, 3x, x" might initially appear deceptively straightforward. However, a deeper dive reveals a fascinating exploration into mathematical patterns, algebraic manipulation, and the power of representation. This article will delve into the intricacies of this sequence, examining its potential interpretations, applications, and underlying principles. We'll explore various scenarios where this pattern might emerge, offering a comprehensive understanding suitable for students and enthusiasts alike.
Understanding the Foundation: What does "x, 3x, x" Represent?
The core of this sequence lies in its inherent ambiguity. The single variable 'x' represents an unknown quantity, a placeholder for a number that could be any real or complex value. The sequence itself doesn't define the nature of 'x' or the context within which it operates. This allows for multiple interpretations and applications, making it a fertile ground for exploration.
The immediate interpretation is a simple arithmetic sequence where the middle term is three times the value of the first and last terms. However, this is just one perspective. Consider the possibility of geometric progressions, recursive relationships, or even contextual applications within specific fields like physics or economics where 'x' might represent a physical quantity or an economic variable.
Scenario 1: The Arithmetic Perspective
If we consider the sequence purely arithmetically, we can analyze it as a simple pattern where the central term is a multiple of the flanking terms. The formula representation would be straightforward:
- Term 1: x
- Term 2: 3x
- Term 3: x
This suggests a repetitive pattern where the value of 'x' remains constant throughout the sequence. The core mathematical relationship here is the multiplicative factor of 3 applied to the first term to generate the second. This simple relationship allows for easy prediction of the sequence's values once the value of 'x' is known. For example:
- If x = 2, the sequence becomes: 2, 6, 2
- If x = 5, the sequence becomes: 5, 15, 5
- If x = -1, the sequence becomes: -1, -3, -1
This arithmetic interpretation is easily understandable and provides a basic framework for working with the sequence. However, we shouldn't limit our understanding to this single perspective.
Scenario 2: Beyond Arithmetic: Exploring Other Interpretations
The beauty of the "x, 3x, x" sequence lies in its potential for broader interpretations. We can move beyond simple arithmetic and consider more complex scenarios:
-
Geometric Progression (with a twist): Although not a classic geometric progression (where each term is multiplied by a constant ratio), we can view this sequence as a modified geometric progression. The ratio between consecutive terms oscillates – 3 for the first step, and 1/3 for the second. This reveals a less obvious, yet equally valid, interpretation of the sequence.
-
Recursive Relationships: We can define the sequence recursively. Let's denote the terms as a₁, a₂, and a₃. Then we can establish a relationship:
- a₁ = x
- a₂ = 3a₁ = 3x
- a₃ = a₁ = x
This recursive definition highlights the cyclical nature of the sequence, where the third term simply repeats the first term. This approach offers an alternative mathematical framework to understand the sequence's structure.
-
Contextual Applications: The meaning of "x, 3x, x" can radically change depending on the context. For example:
-
Physics: Imagine 'x' represents a force applied to an object. The sequence could describe a scenario where a force 'x' is initially applied, then tripled (3x), and finally reverted back to the initial force 'x'.
-
Economics: 'x' could represent a commodity's initial price. The sequence might illustrate price fluctuations: an initial price, a price increase to three times the initial price, and then a price correction back to the original value.
-
Signal Processing: The sequence could represent a discrete signal with specific amplitudes at three distinct points in time.
-
These contextual examples demonstrate the adaptability of the sequence and its potential for representing diverse phenomena. The abstract nature of 'x' empowers its use across multiple disciplines.
Algebraic Manipulation and Solving for 'x'
While determining the value of 'x' requires additional information (a context or an equation involving the terms), we can still explore algebraic manipulations within the sequence itself. For instance, if we're given that the sum of the terms equals a specific value, we can solve for 'x':
Let's say x + 3x + x = 10. Then:
5x = 10
x = 2
This demonstrates how algebraic techniques can be applied to extract information from the sequence, provided sufficient constraints are in place. The sequence becomes a starting point for equation-solving, highlighting the interconnectedness of algebraic principles and numerical patterns.
Expanding the Pattern: Looking Beyond Three Terms
What if we extend the "x, 3x, x" pattern? The most straightforward extension would be a repetition of the three-term sequence: x, 3x, x, x, 3x, x, and so on. However, we could imagine more complex extensions. For example:
-
Adding a constant: We could add a constant 'c' to each term, creating a sequence like: x+c, 3x+c, x+c. This modification introduces an additional variable and increases the complexity.
-
Introducing another variable: We could replace '3' with another variable 'y', giving us: x, yx, x. This generalization allows for a wider range of patterns.
-
Non-linear extensions: We could explore non-linear extensions where the relationship between terms is not simply multiplicative. This opens up the possibility of significantly more complex and interesting patterns.
These variations highlight the flexibility of the "x, 3x, x" sequence as a foundation for constructing more complex mathematical patterns.
The Power of Representation: Visualizing the Sequence
Visual representation can provide valuable insights into the "x, 3x, x" sequence. Imagine plotting the terms on a graph, with the term number on the x-axis and the term value on the y-axis. For any given 'x', you'll get a repeating pattern: a low point, a high point, and then a return to the low point. This visual representation provides an intuitive understanding of the sequence's cyclical nature.
Furthermore, different visualizations can be utilized depending on the context. If 'x' represents a physical quantity over time, a line graph would be appropriate. If 'x' represents a categorical variable, a bar chart could be used. The choice of visualization depends on the interpretation of the sequence and the information one aims to emphasize.
Frequently Asked Questions (FAQ)
Q1: Is the sequence "x, 3x, x" always arithmetic?
No, it's arithmetic only if interpreted in a very specific way. More broadly, it can be considered a modified geometric progression or part of a recursive relationship. The interpretation depends on the context.
Q2: Can 'x' be zero?
Yes, 'x' can be zero. The sequence would then be: 0, 0, 0. This highlights that the sequence is valid even for trivial values of 'x'.
Q3: What if the sequence was "x, x, 3x"? Would the analysis be different?
Yes, the analysis would differ significantly. The order of the terms changes the pattern and its interpretation. This new sequence wouldn't follow the same arithmetic or recursive relationships discussed above.
Q4: What are the real-world applications of this sequence?
The real-world applications are context-dependent. As discussed earlier, the sequence could model various scenarios in physics, economics, signal processing, and other fields. The key is identifying situations where an initial value is tripled and then returns to its original value.
Q5: How can I further explore the potential of this sequence?
Consider exploring different mathematical concepts: Fourier analysis (for analyzing periodic signals), matrix representation (for representing the sequence as a vector), and differential equations (if the sequence represents a continuous process).
Conclusion: Unlocking the Potential of a Simple Sequence
The seemingly simple sequence "x, 3x, x" proves to be surprisingly rich and versatile. By examining its various interpretations—from basic arithmetic to recursive relationships and contextual applications—we've uncovered its hidden potential. The ambiguity of 'x' allows it to adapt to numerous scenarios, making it a powerful tool for representation and modeling across various disciplines. The exploration of this sequence serves as a reminder of the profound mathematical concepts hidden within even the most seemingly straightforward patterns. Further investigation and experimentation are encouraged to fully unlock the potential and applications of this intriguing mathematical sequence. The journey of understanding this simple pattern is a testament to the power of mathematical exploration and the value of looking beyond initial assumptions.
Latest Posts
Latest Posts
-
20 Off 49
Sep 16, 2025
-
Kilopascals To Psi
Sep 16, 2025
-
17 In Binary
Sep 16, 2025
-
98kg Into Stone
Sep 16, 2025
-
41 Of 53
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 3x X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.