17 In Binary
interactiveleap
Sep 16, 2025 · 7 min read
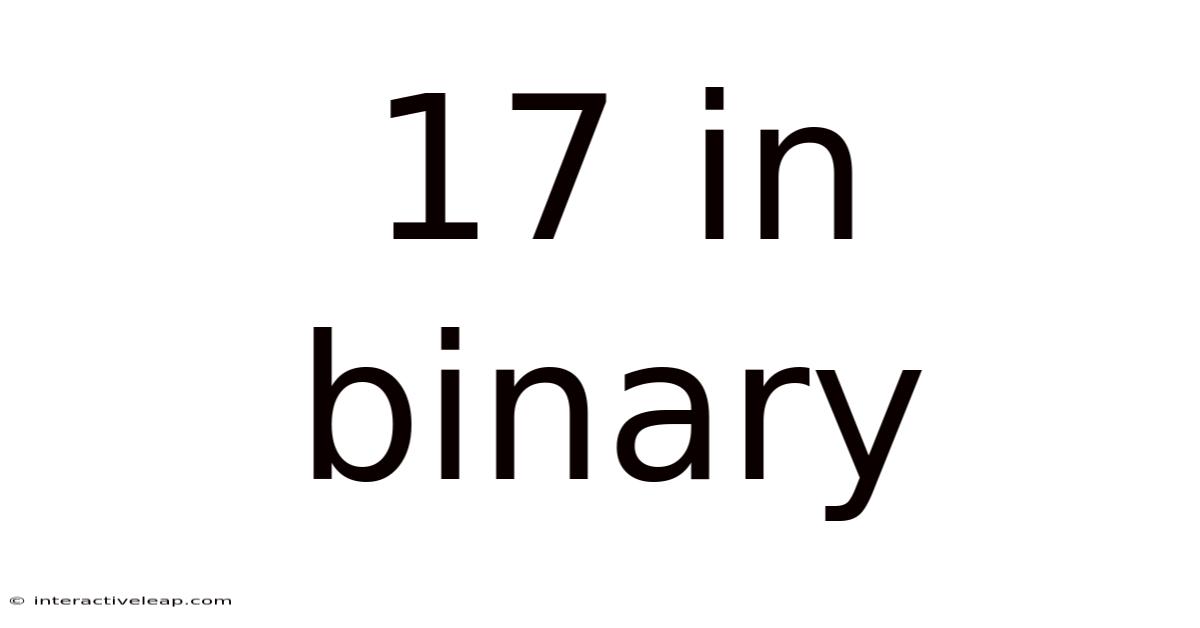
Table of Contents
Decoding 17 in Binary: A Deep Dive into the World of Binary Numbers
Understanding binary numbers is fundamental to comprehending how computers and digital devices function. This article will delve into the fascinating world of binary code, specifically focusing on how the decimal number 17 is represented in binary. We'll explore the conversion process, its underlying principles, and the broader implications of this seemingly simple numerical transformation. This exploration will cover everything from basic binary concepts to practical applications, ensuring a comprehensive understanding for both beginners and those seeking a deeper dive into this crucial area of computer science.
Understanding Binary Numbers: The Foundation
Before we tackle converting 17 to binary, let's establish a solid foundation in binary number systems. Unlike the decimal system (base-10) we use daily, which uses ten digits (0-9), the binary system (base-2) uses only two: 0 and 1. This seemingly simple difference has profound consequences, as it's the language understood by all digital electronics. Each digit in a binary number is called a bit (short for binary digit).
The value of each bit in a binary number depends on its position. Starting from the rightmost bit, each position represents an increasing power of 2. This is analogous to the decimal system where positions represent powers of 10 (ones, tens, hundreds, etc.).
Here's a table illustrating the positional values in binary:
| Position | Power of 2 | Decimal Value |
|---|---|---|
| 0 (Rightmost) | 2⁰ | 1 |
| 1 | 2¹ | 2 |
| 2 | 2² | 4 |
| 3 | 2³ | 8 |
| 4 | 2⁴ | 16 |
| 5 | 2⁵ | 32 |
| 6 | 2⁶ | 64 |
| 7 | 2⁷ | 128 |
| and so on... |
Converting Decimal 17 to Binary: Two Methods
Now, let's convert the decimal number 17 to its binary equivalent. We'll explore two common methods: the division method and the subtraction method.
Method 1: The Division Method (Repeated Division by 2)
This method involves repeatedly dividing the decimal number by 2 and recording the remainders. The remainders, read in reverse order, form the binary representation.
- Divide 17 by 2: 17 ÷ 2 = 8 with a remainder of 1.
- Divide 8 by 2: 8 ÷ 2 = 4 with a remainder of 0.
- Divide 4 by 2: 4 ÷ 2 = 2 with a remainder of 0.
- Divide 2 by 2: 2 ÷ 2 = 1 with a remainder of 0.
- Divide 1 by 2: 1 ÷ 2 = 0 with a remainder of 1.
Reading the remainders from bottom to top, we get 10001. Therefore, 17 in decimal is 10001 in binary.
Method 2: The Subtraction Method (Subtracting Powers of 2)
This method involves subtracting the highest possible power of 2 from the decimal number and repeating the process with the remaining value.
- Start with the largest power of 2 less than or equal to 17: This is 16 (2⁴).
- Subtract 16 from 17: 17 - 16 = 1.
- The remaining value is 1: The only power of 2 less than or equal to 1 is 1 (2⁰).
- Subtract 1 from 1: 1 - 1 = 0.
We subtracted 16 (represented by a '1' in the 2⁴ position) and 1 (represented by a '1' in the 2⁰ position). The other positions (2³, 2², 2¹) have a value of 0 because we didn't subtract them. This gives us the binary representation: 10001.
Verification and Understanding the Result: 10001₂
Let's verify our result by expanding the binary number 10001₂ (the subscript '₂' indicates a binary number):
(1 × 2⁴) + (0 × 2³) + (0 × 2²) + (0 × 2¹) + (1 × 2⁰) = 16 + 0 + 0 + 0 + 1 = 17₁₀ (the subscript '₁₀' indicates a decimal number)
This confirms that our conversion is correct. The binary number 10001 represents the decimal value 17 through the weighted sum of its bits.
Beyond the Basics: Binary Representation and Computer Architecture
The representation of 17 as 10001 highlights a key aspect of how computers work. Computers store and process information using sequences of bits, representing everything from numbers and text to images and videos. These bits are physically represented by electronic signals (high voltage representing 1 and low voltage representing 0) within the computer's circuitry. The way these bits are grouped and interpreted determines the meaning of the data.
For example, a single byte (8 bits) can represent 2⁸ = 256 different values. This capacity is fundamental to encoding characters, colors, and various other data types within computer systems. The architecture of the CPU (Central Processing Unit) is designed to efficiently perform operations on these binary representations. This includes performing arithmetic operations (addition, subtraction, multiplication, division), logical operations (AND, OR, NOT), and data manipulation.
Applications of Binary Numbers: A Glimpse into the Digital World
The seemingly simple concept of binary numbers underpins a vast array of technologies that we use daily. Here are a few examples:
- Computer Memory: RAM (Random Access Memory) and ROM (Read-Only Memory) store data in binary format. Every piece of information – from operating system instructions to your favorite video game – is ultimately a sequence of 0s and 1s.
- Digital Images: Images are represented digitally by assigning binary codes to each pixel, defining its color and intensity. Higher resolution images require more bits to represent the finer details.
- Audio and Video: Sound and video data are also encoded in binary. Digital audio files (like MP3s) and video files (like MP4s) are essentially long sequences of bits representing sound waves and image frames.
- Network Communication: All data transmitted over networks – the internet, for example – is encoded in binary. Protocols like TCP/IP rely on the consistent and reliable transmission of binary data packets.
Frequently Asked Questions (FAQs)
Q: Why do computers use binary instead of decimal?
A: Computers use binary because it's easier and more reliable to build electronic circuits that represent two distinct states (0 and 1) than circuits representing ten distinct states (0-9). The inherent simplicity and robustness of binary make it ideal for digital electronics.
Q: Can binary numbers represent negative numbers?
A: Yes, there are several methods for representing negative numbers in binary, such as two's complement and sign-magnitude. These methods utilize the most significant bit (leftmost bit) to indicate the sign (0 for positive, 1 for negative) and modify the representation of the magnitude accordingly.
Q: What about other number systems like hexadecimal and octal?
A: Hexadecimal (base-16) and octal (base-8) are often used as shorthand representations of binary numbers. They are more concise than binary, making them easier to read and write, but they are still ultimately based on the binary system. Hexadecimal uses digits 0-9 and letters A-F (representing 10-15), while octal uses digits 0-7. These systems offer a convenient way to represent large binary numbers more compactly.
Q: How are floating-point numbers represented in binary?
A: Floating-point numbers (like 3.14159) are represented in binary using a standard like IEEE 754. This standard uses a specific format to store the sign, mantissa (significant digits), and exponent of the number in binary. This allows for the representation of both very large and very small numbers.
Q: Is learning binary important for everyone?
A: While a deep understanding of binary is primarily crucial for computer scientists, software engineers, and electrical engineers, having a basic understanding of its principles is beneficial for anyone in today's increasingly digital world. It helps demystify how computers and digital devices function, providing a fundamental understanding of the underlying technology.
Conclusion: The Significance of Binary in the Digital Age
The conversion of 17 to its binary equivalent, 10001, is far more than a simple mathematical exercise. It's a window into the fundamental language of computers and the digital world. By grasping the principles of binary representation, we gain a deeper appreciation for how computers process information, store data, and ultimately power the technology that shapes our modern lives. From the smallest microcontrollers to the most powerful supercomputers, the ubiquitous 0s and 1s of binary code are the building blocks of the digital age. This foundational knowledge empowers us to better understand, engage with, and even contribute to the ever-evolving landscape of computing.
Latest Posts
Latest Posts
-
20 Off 14 00
Sep 16, 2025
-
6 Of 300
Sep 16, 2025
-
Charge For Zinc
Sep 16, 2025
-
64 Square Rooted
Sep 16, 2025
-
2 9 Cos 17
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 17 In Binary . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.