2.9 Cos 17
interactiveleap
Sep 16, 2025 · 6 min read
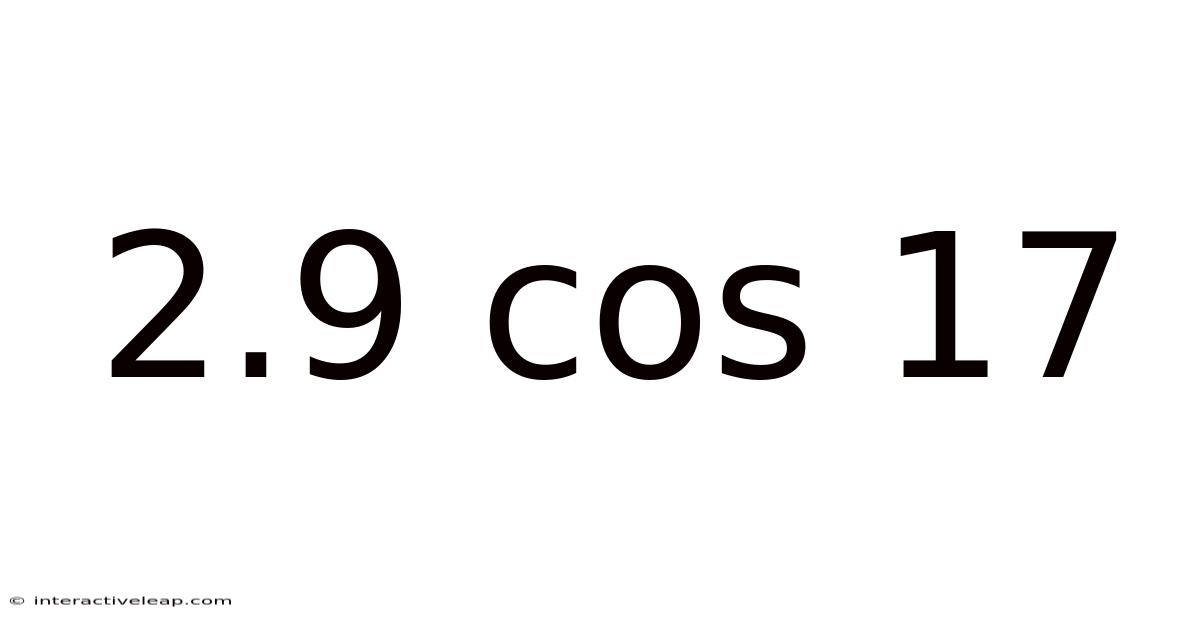
Table of Contents
Decoding 2.9 cos 17: A Deep Dive into Trigonometry and its Applications
This article delves into the meaning and calculation of the expression "2.9 cos 17," explaining the underlying trigonometric concepts and demonstrating its relevance in various fields. We'll explore the fundamentals of trigonometry, the use of calculators and software for computation, and real-world applications where such calculations are crucial. Understanding this seemingly simple expression opens doors to a world of complex problem-solving in engineering, physics, and computer science.
Understanding the Basics: Trigonometry and the Cosine Function
At the heart of "2.9 cos 17" lies trigonometry, the branch of mathematics dealing with the relationships between angles and sides of triangles. The expression involves the cosine function, one of the three primary trigonometric functions (sine, cosine, and tangent).
The cosine of an angle in a right-angled triangle is defined as the ratio of the length of the adjacent side to the length of the hypotenuse. However, the cosine function's domain extends beyond right-angled triangles. In a broader context, it can be defined using the unit circle in coordinate geometry, where the cosine of an angle represents the x-coordinate of a point on the circle.
Key Concepts:
-
Angle Measurement: The "17" in "2.9 cos 17" represents an angle. Unless otherwise specified, this angle is assumed to be measured in degrees. Radians are another common unit for angle measurement, particularly in advanced mathematical contexts. It's crucial to ensure your calculator is set to the correct angle mode (degrees or radians).
-
Cosine Function: The cosine function, denoted as cos(θ), where θ is the angle, produces a value between -1 and 1. The value depends solely on the angle provided. For example, cos(0°) = 1, cos(90°) = 0, and cos(180°) = -1. The cosine function is periodic, meaning its values repeat every 360° (or 2π radians).
-
Scalar Multiplication: The "2.9" in "2.9 cos 17" represents scalar multiplication. This simply means multiplying the result of the cosine function by the constant 2.9. This scaling factor changes the magnitude of the final result but doesn't alter the underlying trigonometric relationship.
Calculating 2.9 cos 17: Methods and Tools
Calculating "2.9 cos 17" requires a scientific calculator or mathematical software. Here's how to perform the calculation:
1. Using a Scientific Calculator:
- Ensure your calculator is set to degree mode.
- Enter "17" and press the "cos" button. This will give you the cosine of 17 degrees.
- Multiply the result by 2.9.
The result, rounded to several decimal places, is approximately 2.776.
2. Using Mathematical Software (e.g., MATLAB, Python):
Most mathematical software packages have built-in trigonometric functions. For example, in Python:
import math
result = 2.9 * math.cos(math.radians(17))
print(result)
Note that the math.radians() function converts the angle from degrees to radians, as Python's trigonometric functions typically operate in radians.
The Significance of Precision: Rounding and Error
When dealing with trigonometric calculations, the level of precision is important. The accuracy of the final answer depends on the precision of the input angle and the calculator or software used. Rounding errors can accumulate, particularly in complex calculations involving multiple trigonometric functions. While 2.776 is a reasonable approximation, higher precision may be required for certain applications. For instance, engineering projects often require calculations to several decimal places to ensure accuracy and safety.
Real-World Applications: Where 2.9 cos 17 Might Appear
While the expression "2.9 cos 17" might seem abstract, it represents a fundamental type of calculation found in many fields:
1. Physics and Engineering:
Trigonometry is essential in physics and engineering for analyzing vectors and forces. Consider a scenario involving a force vector with a magnitude of 2.9 units acting at an angle of 17 degrees to the horizontal. The horizontal component of this force would be calculated as 2.9 cos 17. This concept is crucial in:
- Mechanics: Calculating the components of forces acting on objects.
- Electronics: Analyzing alternating current (AC) circuits.
- Civil Engineering: Determining structural forces and stability.
- Projectile Motion: Calculating the horizontal displacement of a projectile.
2. Computer Graphics and Game Development:
Trigonometric functions are fundamental in computer graphics and game development for:
- Transformations: Rotating, scaling, and translating objects on screen.
- Animation: Creating smooth and realistic movements.
- Lighting and Shading: Calculating the intensity of light hitting surfaces.
- Collision Detection: Determining whether objects are colliding.
3. Surveying and Navigation:
Trigonometry plays a vital role in determining distances, heights, and positions. Calculations similar to "2.9 cos 17" are used in:
- Surveying land: Measuring distances and angles.
- GPS Navigation: Calculating positions based on satellite signals.
- Mapping and Cartography: Creating accurate maps and charts.
4. Signal Processing:
Trigonometric functions are fundamental to signal processing techniques, including:
- Fourier Analysis: Decomposing complex signals into simpler sinusoidal components.
- Digital Signal Processing (DSP): Filtering and manipulating digital signals.
Beyond the Basics: Expanding the Understanding
The expression "2.9 cos 17" serves as a gateway to a much richer understanding of trigonometry and its applications. While we focused on the cosine function, the sine and tangent functions are equally important and used extensively in similar applications. Furthermore, more advanced trigonometric concepts like inverse functions (arcsin, arccos, arctan), identities, and laws of sines and cosines are crucial for solving more complex problems.
Frequently Asked Questions (FAQ)
Q: What if the angle were in radians instead of degrees?
A: If the angle were in radians, you would need to ensure your calculator is set to radian mode before performing the calculation. Alternatively, you could convert the angle from radians to degrees using the conversion factor (180°/π).
Q: Can this calculation be done without a calculator?
A: Precisely calculating cos 17° without a calculator is difficult. However, you could use trigonometric identities and approximations to get an estimate. This is generally not practical for most real-world applications.
Q: What are some common errors to avoid when using trigonometric functions?
A: Common errors include: using the incorrect angle mode (degrees vs. radians), incorrect input of the angle value, and neglecting the sign of trigonometric functions in different quadrants.
Conclusion: The Power of a Simple Expression
The seemingly simple expression "2.9 cos 17" encapsulates the power and versatility of trigonometry. It’s a foundational element in a wide array of scientific and technological fields. Understanding this calculation, along with the underlying principles of trigonometry, opens doors to a deeper appreciation of how mathematics shapes our world and solves complex problems. From the physics of motion to the artistry of computer graphics, the influence of trigonometric functions is undeniable. This article serves as a starting point for further exploration into this fascinating and essential branch of mathematics. Further investigation into advanced trigonometric concepts and their applications is highly recommended for those seeking a more comprehensive understanding.
Latest Posts
Latest Posts
-
10 Of 190
Sep 16, 2025
-
82 7kg In Stone
Sep 16, 2025
-
Esd Wrist Strap
Sep 16, 2025
-
64 1kg In Lbs
Sep 16, 2025
-
A Hostile Environment
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2.9 Cos 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.