7/15 X 360
interactiveleap
Sep 16, 2025 · 5 min read
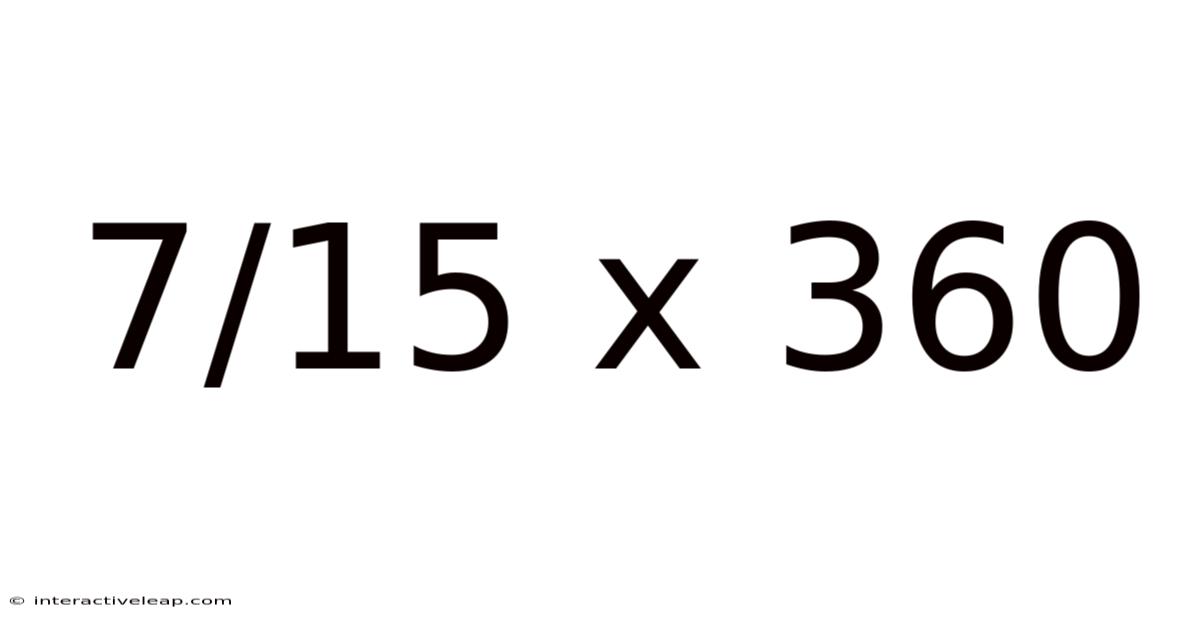
Table of Contents
Decoding 7/15 x 360: A Deep Dive into Fraction Multiplication and its Applications
This article explores the seemingly simple calculation of 7/15 x 360, delving far beyond the immediate answer. We will unravel the process of multiplying fractions by whole numbers, explaining the underlying mathematical principles, showcasing practical applications, and addressing common misconceptions. This comprehensive guide will equip you with a thorough understanding of this fundamental arithmetic operation, making you confident in tackling similar problems and appreciating the broader context of fractions in mathematics and real-world scenarios.
Introduction: Understanding Fraction Multiplication
At its core, the problem 7/15 x 360 involves multiplying a fraction (7/15) by a whole number (360). This operation represents a fundamental concept in mathematics with widespread applications in various fields. Understanding fraction multiplication is crucial for mastering more advanced mathematical concepts and solving real-world problems involving proportions, ratios, and percentages.
Before diving into the calculation, let's review the basics of fraction multiplication. When multiplying fractions, we multiply the numerators (top numbers) together and the denominators (bottom numbers) together. For example, (a/b) x (c/d) = (a x c) / (b x d). When multiplying a fraction by a whole number, we can rewrite the whole number as a fraction with a denominator of 1. This allows us to apply the same rule of multiplying numerators and denominators. Therefore, (a/b) x c = (a/b) x (c/1) = (a x c) / (b x 1).
Step-by-Step Calculation of 7/15 x 360
Now, let's tackle the problem at hand: 7/15 x 360.
-
Rewrite the whole number as a fraction: We rewrite 360 as 360/1. Our problem now becomes (7/15) x (360/1).
-
Multiply the numerators: Multiply the numerators: 7 x 360 = 2520.
-
Multiply the denominators: Multiply the denominators: 15 x 1 = 15.
-
Form the resulting fraction: This gives us the fraction 2520/15.
-
Simplify the fraction: This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 2520 and 15 is 15. Dividing both the numerator and the denominator by 15, we get: 2520 ÷ 15 = 168 and 15 ÷ 15 = 1.
-
Final Answer: Therefore, 7/15 x 360 = 168.
Alternative Calculation Methods: Simplifying Before Multiplication
We can often simplify the calculation by canceling common factors before multiplying. This method reduces the numbers involved, making the calculation easier and less prone to errors.
Let's revisit (7/15) x (360/1). Notice that 360 can be divided by 15. Performing this division simplifies the process significantly.
-
Simplify before multiplying: We can simplify the fraction by dividing both 360 (the numerator of 360/1) and 15 (the denominator of 7/15) by their greatest common divisor, which is 15. This results in:
(7/1) x (24/1)
-
Multiply the simplified fractions: Now, multiplying the numerators and denominators becomes considerably simpler: 7 x 24 = 168. The denominator remains 1.
-
Final Answer: The final answer, as before, is 168.
This approach demonstrates that strategic simplification can dramatically ease complex calculations.
Explanation of the Mathematical Principles Involved
This calculation hinges on several key mathematical principles:
- Fraction Multiplication: The fundamental rule of multiplying numerators and denominators.
- Equivalent Fractions: The process of simplifying the fraction 2520/15 relies on the concept of equivalent fractions. We find a common factor (15) and divide both the numerator and the denominator by that factor, resulting in a simpler, equivalent fraction (168/1).
- Greatest Common Divisor (GCD): Finding the GCD allows us to simplify fractions to their lowest terms, making them easier to work with and providing a more concise representation of the value.
- Commutative Property of Multiplication: The order in which we multiply the numbers doesn't affect the result. This is crucial when simplifying before multiplying; we can rearrange the terms to make the cancellation easier.
Practical Applications of Fraction Multiplication
Fraction multiplication finds extensive use in various real-world scenarios:
-
Calculating Percentages: Finding a percentage of a quantity is a direct application of fraction multiplication. For example, finding 7/15 of 360 could represent finding 46.67% (7/15 expressed as a percentage) of 360.
-
Scaling and Proportions: Many recipes and construction plans involve scaling ingredients or dimensions proportionally. If a recipe requires 7/15 of a cup of sugar for a certain yield, scaling up requires multiplying the fraction by the desired increase factor.
-
Measurement Conversions: Converting units of measurement (like inches to centimeters or pounds to kilograms) often involves multiplication by a fractional conversion factor.
-
Financial Calculations: Dividing profits or expenses proportionally among partners or shareholders involves fraction multiplication.
-
Data Analysis: Calculating proportions or percentages within datasets frequently employs fraction multiplication.
Frequently Asked Questions (FAQs)
Q: Can I use a calculator to solve 7/15 x 360?
A: Yes, absolutely. Most calculators can handle fraction multiplication directly. However, understanding the manual calculation process is essential for building a solid foundation in mathematics and for situations where a calculator might not be available.
Q: What if the fraction and whole number are larger or more complex?
A: The same principles apply. Rewrite the whole number as a fraction, multiply the numerators and denominators, and simplify the resulting fraction. Always look for opportunities to simplify before multiplying to reduce calculation complexity.
Q: What if the fraction is an improper fraction (numerator is larger than the denominator)?
A: The process remains the same. Multiply the numerators and denominators, and then simplify the result. An improper fraction often simplifies to a whole number or a mixed number (whole number and a fraction).
Q: Why is simplification important?
A: Simplification makes the fraction easier to understand and use. It provides a more concise representation of the value and can significantly reduce the complexity of subsequent calculations involving the fraction.
Conclusion: Mastering Fraction Multiplication
The seemingly simple calculation of 7/15 x 360 provides a gateway to understanding the broader world of fractions and their applications. By mastering the techniques of fraction multiplication and simplification, you equip yourself with a valuable skill applicable across various mathematical and real-world problems. Remember to utilize simplification strategies to enhance efficiency and accuracy. Through consistent practice and a deeper understanding of the underlying principles, you can confidently navigate the world of fractions and utilize this essential arithmetic tool effectively. The ability to perform these calculations efficiently will pave the way for success in more advanced mathematical concepts and practical applications.
Latest Posts
Latest Posts
-
Radar Excel Chart
Sep 16, 2025
-
80 Of 8
Sep 16, 2025
-
1 74cm In Feet
Sep 16, 2025
-
4 Of 80000
Sep 16, 2025
-
125g Into Ounces
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 7/15 X 360 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.