20 Of 18.00
interactiveleap
Sep 16, 2025 · 6 min read
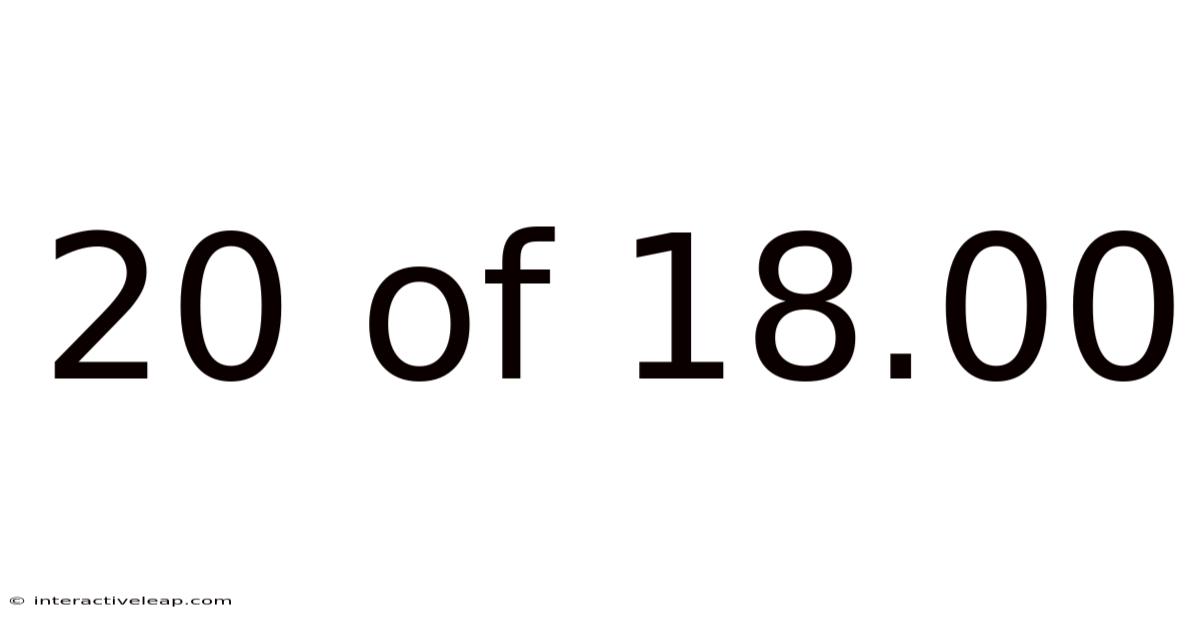
Table of Contents
Decoding 20 of 18.00: A Deep Dive into Odds, Probability, and Real-World Applications
The seemingly simple expression "20 of 18.00" might initially seem perplexing. It's not a standard mathematical equation, but rather a representation of odds, often encountered in gambling, sports betting, and even risk assessment. This article will dissect the meaning of "20 of 18.00," exploring its underlying principles, calculating implied probability, and examining its practical applications across diverse fields. Understanding this concept unlocks a deeper understanding of probability and its role in decision-making.
Understanding the Basics: Odds vs. Probability
Before diving into "20 of 18.00," let's clarify the fundamental difference between odds and probability. While both relate to the likelihood of an event, they express this likelihood in different ways.
-
Probability: Probability represents the likelihood of an event occurring as a fraction between 0 and 1 (or as a percentage between 0% and 100%). A probability of 0.5 (or 50%) means the event is equally likely to occur as not to occur.
-
Odds: Odds express the likelihood of an event as a ratio of favorable outcomes to unfavorable outcomes. For example, odds of 2:1 mean there are two favorable outcomes for every one unfavorable outcome.
The key difference lies in the focus: probability focuses on the likelihood of success, while odds focus on the ratio of success to failure. They are, however, mathematically related and can be easily converted from one to the other.
Deciphering "20 of 18.00": A Fractional Representation of Odds
The expression "20 of 18.00" represents odds in a slightly unusual fractional format. It's essentially stating that for every 20 units wagered, a potential return of 18.00 units is expected if the event occurs. This format is sometimes used in contexts where the initial stake isn't explicitly separated from the potential profit. Therefore, we can represent this more conventionally as odds of 18:20, or simplified to 9:10.
This means that for every 10 units risked, a potential profit of 9 units is anticipated. This is not a guaranteed win, however. This represents the offered odds, often set by a bookmaker or institution considering factors like the perceived likelihood of the event and potential profit margins.
Calculating Implied Probability from Odds
The odds provided (9:10) can be converted into an implied probability. The formula is as follows:
Implied Probability = Favorable Outcomes / (Favorable Outcomes + Unfavorable Outcomes)
In our case:
Implied Probability = 9 / (9 + 10) = 9/19 ≈ 0.474 or 47.4%
This means the bookmaker assessing "20 of 18.00" odds believes there's approximately a 47.4% chance of the event occurring. The remaining 52.6% represents the bookmaker's margin or "overround." This overround is how bookmakers make a profit; they consistently set odds that slightly underestimate the true probability of events.
Real-World Applications and Interpretations
The concept of "20 of 18.00" or similar odd representations finds application in various fields:
-
Sports Betting: This is the most common context. Bookmakers use odds to determine potential payouts for various sports events. Understanding implied probability helps bettors assess whether the offered odds reflect the true likelihood of an event and whether a bet offers value.
-
Financial Markets: Odds-like representations are used in options trading and other derivative markets. Implied volatility, for example, can be viewed as a measure of the market's perception of the likelihood of price movements.
-
Risk Assessment: In insurance and risk management, odds are used to quantify the likelihood of various events (e.g., accidents, natural disasters). This helps in setting premiums and developing risk mitigation strategies.
-
Gambling: Casinos and lotteries use odds to structure games and determine payouts. Understanding the odds allows players to assess the potential returns relative to the risk involved.
-
Data Science and Machine Learning: Probability and odds are central to many machine learning algorithms used for prediction and classification. Models often output probabilities, which can be converted into odds to provide a more intuitive interpretation.
The Importance of Considering the "Overround"
It's crucial to remember that the odds offered by bookmakers or institutions rarely reflect the true probability of an event. The "overround" built into the odds ensures profitability for the entity offering them. A higher overround implies a larger profit margin for the bookmaker and potentially a less favorable bet for the player.
For example, if you were to bet on every possible outcome of a horse race using these odds and the true probabilities were perfectly reflected, you would lose money on average. This is because the sum of the implied probabilities (considering all possible outcomes) will exceed 100% due to the overround. Understanding the overround is key to making informed decisions.
Advanced Considerations: Dealing with Multiple Events
When dealing with multiple events, the calculation of probabilities becomes more complex. We need to consider the relationships between events (are they independent, mutually exclusive, etc.) For instance, the probability of two independent events both occurring is the product of their individual probabilities. If we are dealing with "20 of 18.00" odds for multiple events, the calculation of overall implied probability will require a detailed understanding of the dependencies between those events.
FAQ: Frequently Asked Questions
Q1: What if the odds are expressed differently, say as a decimal?
A1: Decimal odds represent the total return for a 1 unit stake. For example, decimal odds of 2.0 mean a 1 unit stake would return 2 units (1 unit profit + 1 unit stake). To convert decimal odds to implied probability, use the formula: Implied Probability = 1 / Decimal Odds.
Q2: How can I identify value bets using these odds?
A2: A value bet is one where the implied probability is lower than your own assessment of the true probability. If you believe the true probability of an event is higher than the implied probability derived from the offered odds, then the bet is considered to have value.
Q3: Are there limitations to using implied probability?
A3: Yes, implied probability is only as good as the model or assumptions used to determine the underlying odds. Inaccurate models or unforeseen circumstances can lead to inaccurate implied probabilities. Additionally, implied probability doesn’t account for factors like emotional biases in decision-making.
Conclusion: Unlocking the Power of "20 of 18.00"
The seemingly simple phrase "20 of 18.00" unveils a world of probability, odds, and their applications in diverse fields. By understanding the relationship between odds and probability, calculating implied probabilities, and recognizing the implications of the overround, we can make more informed decisions in scenarios involving risk and uncertainty. While the specific context matters, the underlying principles remain consistent, allowing for insightful analysis across various applications from sports betting to financial modeling. This detailed understanding empowers individuals to navigate these scenarios more effectively, making sound judgments based on a solid grasp of statistical concepts. It's not just about numbers; it's about understanding the power of probability in shaping our world.
Latest Posts
Latest Posts
-
Radar Excel Chart
Sep 16, 2025
-
80 Of 8
Sep 16, 2025
-
1 74cm In Feet
Sep 16, 2025
-
4 Of 80000
Sep 16, 2025
-
125g Into Ounces
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 18.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.