1.5 X 7
interactiveleap
Sep 21, 2025 · 6 min read
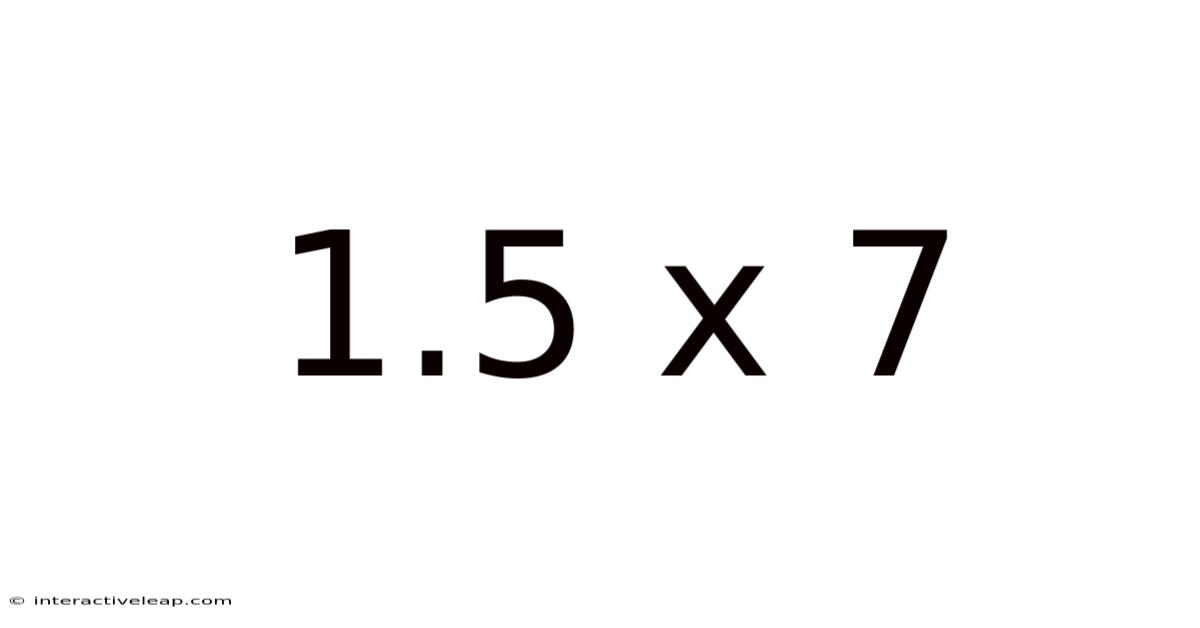
Table of Contents
Decoding 1.5 x 7: Exploring the Mathematical Concept and its Real-World Applications
This article delves into the seemingly simple mathematical expression "1.5 x 7," exploring its fundamental calculation, its relevance within broader mathematical concepts, and its surprising applications in various real-world scenarios. We'll move beyond the basic arithmetic to uncover the deeper understanding and practical implications of this seemingly straightforward equation. Understanding this simple multiplication problem can unlock a deeper appreciation for mathematics and its pervasive influence on our daily lives.
Understanding the Fundamentals: Calculating 1.5 x 7
At its core, "1.5 x 7" represents a multiplication problem. It asks: "What is the result of multiplying 1.5 (one and a half) by 7?" The most straightforward approach involves converting 1.5 into a fraction: 3/2. This transforms the problem into (3/2) x 7. Multiplying the numerator (3) by 7 gives us 21, and the denominator (2) remains unchanged, resulting in the fraction 21/2.
To convert this improper fraction back into a decimal, we perform the division: 21 divided by 2 equals 10.5. Therefore, 1.5 x 7 = 10.5.
Alternatively, we can perform the multiplication directly using decimals:
- Multiply 1.5 by 7, ignoring the decimal point initially: 15 x 7 = 105
- Count the total number of digits after the decimal point in the original numbers (one digit in 1.5).
- Place the decimal point in the result (105) so that there is one digit after the decimal point: 10.5
Both methods yield the same answer, highlighting the flexibility and interconnectedness of mathematical operations.
Expanding the Concept: Beyond Basic Multiplication
While the calculation itself is elementary, understanding "1.5 x 7" allows us to explore more complex mathematical ideas. This seemingly simple equation opens doors to understanding:
-
Fractions and Decimals: The problem seamlessly integrates fractions and decimals, reinforcing the relationship between these two representations of numbers. Converting between fractions and decimals is a crucial skill in various mathematical contexts.
-
Multiplication as Repeated Addition: Multiplication can be visualized as repeated addition. 1.5 x 7 is equivalent to adding 1.5 seven times: 1.5 + 1.5 + 1.5 + 1.5 + 1.5 + 1.5 + 1.5 = 10.5. This provides a concrete understanding of the concept of multiplication.
-
Distributive Property: The distributive property states that a(b + c) = ab + ac. We could break down 1.5 into 1 + 0.5 and apply the distributive property: (1 + 0.5) x 7 = (1 x 7) + (0.5 x 7) = 7 + 3.5 = 10.5. This illustrates the flexibility and power of algebraic manipulation.
-
Proportions and Ratios: The equation can be used to solve problems involving proportions and ratios. For example, if one item costs 1.5 units of currency, the cost of 7 such items would be 1.5 x 7 = 10.5 units of currency.
-
Scaling and Linear Relationships: The multiplication reflects a linear relationship. If we think of 7 as a quantity and 1.5 as a scaling factor, the result 10.5 represents the scaled quantity. This principle is fundamental in many applications, including scaling images, adjusting recipes, and understanding growth rates.
Real-World Applications: Where 1.5 x 7 Matters
The seemingly simple calculation of 1.5 x 7 has surprisingly widespread applications in various real-world scenarios. Let's explore a few:
-
Shopping and Budgeting: Imagine buying 7 items, each costing $1.50. The total cost is 1.5 x 7 = $10.50. This simple calculation is fundamental to daily budgeting and financial planning.
-
Cooking and Baking: Recipes often require scaling up or down. If a recipe calls for 1.5 cups of flour and you want to make seven times the recipe, you need 1.5 x 7 = 10.5 cups of flour.
-
Construction and Measurement: In construction, precise measurements are crucial. If a particular task requires 1.5 meters of material and you need to repeat this 7 times, you'll need 10.5 meters of material.
-
Travel and Distance: If you travel at an average speed of 1.5 kilometers per minute for 7 minutes, you will cover 10.5 kilometers.
-
Data Analysis and Statistics: In data analysis, scaling and normalization of data are common practices. Multiplying data points by a constant factor, like 1.5, might be necessary for certain statistical analyses.
-
Graphic Design and Image Manipulation: When scaling images or graphics, the dimensions are often adjusted by a factor. If you need to scale the width of an image by 1.5 and it's originally 7 units wide, the new width will be 10.5 units.
-
Manufacturing and Production: In manufacturing, calculating the amount of raw materials needed for a certain number of products often involves such simple multiplications. If each product requires 1.5 units of a specific component and you need to produce 7 products, you'll need 10.5 units of that component.
-
Finance and Investment: Simple interest calculations often involve multiplying the principal amount by the interest rate and the time period. This basic multiplication forms the foundation of more complex financial calculations.
Exploring Further: Expanding the Scope
The equation 1.5 x 7 can serve as a springboard for exploring more advanced mathematical concepts. For instance:
-
Algebraic Expressions: We can represent the equation algebraically as 1.5x = y, where x = 7 and y = 10.5. This introduces the concept of variables and equations, fundamental to algebra.
-
Functions: The relationship between 1.5 and 7 can be represented as a function: f(x) = 1.5x. This function maps an input value (x) to an output value (y = 1.5x). Understanding functions is crucial for calculus and higher-level mathematics.
-
Geometry and Area: Imagine a rectangle with a width of 1.5 units and a length of 7 units. The area of this rectangle would be 1.5 x 7 = 10.5 square units. This extends the concept into geometric applications.
Frequently Asked Questions (FAQ)
Q: What are some alternative ways to calculate 1.5 x 7?
A: Besides the methods already described, you can use a calculator, break down 1.5 into 1 + 0.5 and multiply separately, or use long multiplication. The choice depends on the context and available tools.
Q: Why is it important to understand the concept behind the calculation, not just the answer?
A: Understanding the underlying principles allows you to apply the same logic to similar problems with different numbers, solve problems in various contexts, and develop a deeper understanding of mathematics.
Q: Can this concept be applied to negative numbers?
A: Yes, the same principles apply. For example, 1.5 x (-7) = -10.5. The rules of multiplying positive and negative numbers need to be considered.
Q: How does this simple equation relate to more complex mathematical concepts?
A: It forms the basis for understanding more advanced topics like algebra, calculus, and even linear algebra, showcasing the interconnectedness of mathematical concepts.
Conclusion: The Power of Simplicity
The seemingly simple equation "1.5 x 7" reveals a wealth of mathematical concepts and practical applications. From basic arithmetic to the intricacies of scaling and linear relationships, understanding this equation fosters a deeper appreciation for the interconnectedness of mathematical ideas and their pervasive influence on our daily lives. By exploring this simple equation, we uncover the power of mathematical understanding, its practical utility, and its potential to unlock a wider appreciation of the world around us. The seemingly insignificant calculation is, in fact, a powerful microcosm of the broader mathematical world, highlighting the value of understanding not just the answer but the underlying principles.
Latest Posts
Latest Posts
-
Rdm Meaning Gta
Sep 21, 2025
-
Antonyms For Reservoir
Sep 21, 2025
-
35 Of 15
Sep 21, 2025
-
18 5 6
Sep 21, 2025
-
55 Of 20
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1.5 X 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.