35 Of 15
interactiveleap
Sep 21, 2025 · 5 min read
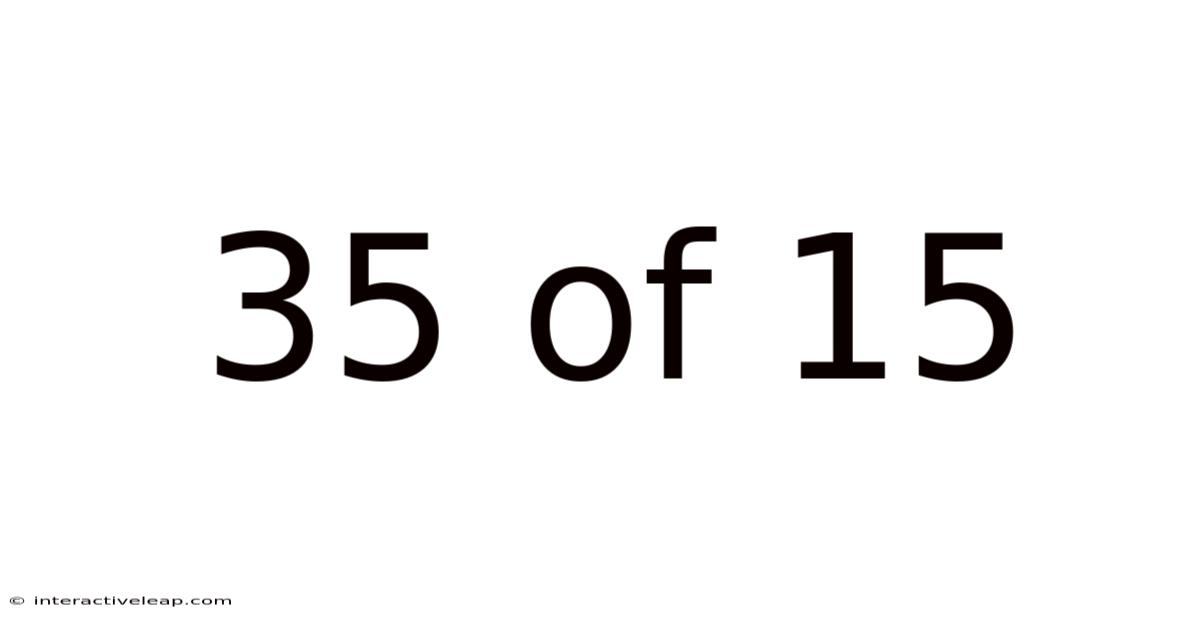
Table of Contents
Understanding the Fraction 35/15: A Deep Dive into Simplification, Decimals, and Real-World Applications
The fraction 35/15 might seem simple at first glance, but it holds a wealth of mathematical concepts that extend far beyond its basic form. This article will explore the intricacies of this fraction, guiding you through simplification, decimal conversion, real-world applications, and addressing common misconceptions. We'll delve into the underlying principles, ensuring a comprehensive understanding suitable for learners of all levels. This exploration will cover topics such as fraction simplification, decimal representation, improper fractions, and mixed numbers, providing a robust understanding of this seemingly simple fraction.
Understanding Fractions: A Quick Recap
Before we dive into the specifics of 35/15, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator represents how many of those parts are being considered.
For example, in the fraction 1/4, the denominator (4) indicates that the whole is divided into four equal parts, and the numerator (1) indicates that we are considering one of those parts.
Simplifying the Fraction 35/15
The fraction 35/15 is an improper fraction because the numerator (35) is larger than the denominator (15). Improper fractions are perfectly valid, but they can often be simplified or converted into a more manageable form. Simplification involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both numbers without leaving a remainder.
To find the GCD of 35 and 15, we can list the factors of each number:
- Factors of 35: 1, 5, 7, 35
- Factors of 15: 1, 3, 5, 15
The largest common factor is 5. Therefore, we divide both the numerator and the denominator by 5:
35 ÷ 5 = 7 15 ÷ 5 = 3
This simplifies 35/15 to 7/3. This simplified fraction is still an improper fraction, but it's in its simplest form.
Converting to a Mixed Number
An improper fraction can also be converted into a mixed number, which combines a whole number and a proper fraction. To do this, we perform division:
7 ÷ 3 = 2 with a remainder of 1
The quotient (2) becomes the whole number, and the remainder (1) becomes the numerator of the new fraction, while the denominator remains the same (3). Therefore, 7/3 is equivalent to 2 1/3.
Decimal Representation of 35/15
To express 35/15 as a decimal, we can divide the numerator by the denominator:
35 ÷ 15 = 2.333...
This decimal is a repeating decimal, indicated by the ellipsis (...). The digit 3 repeats infinitely. This can also be written as 2.3̅.
Real-World Applications of 35/15 and Related Concepts
Fractions are fundamental to numerous real-world applications. Let's explore some examples where understanding 35/15 and its related concepts are crucial:
-
Baking and Cooking: Recipes often require fractional measurements. If a recipe calls for 35 grams of sugar and you only have a scale that measures in 15-gram increments, you'd need to understand how to work with the fraction 35/15 to determine the correct amount.
-
Construction and Engineering: Accurate measurements are paramount. Fractions are used extensively in blueprints and calculations to ensure precise dimensions and structural integrity. Understanding how to simplify and convert fractions is vital for accuracy.
-
Finance and Budgeting: Managing personal finances frequently involves dealing with fractions, such as calculating percentages, proportions, and interest rates. Converting fractions to decimals facilitates easier calculations.
-
Data Analysis and Statistics: Fractions and decimals are essential tools in representing and analyzing data. Understanding proportions and ratios is crucial for interpreting statistical findings.
-
Measurement and Science: Many scientific measurements involve fractions and decimals. Understanding these concepts is vital in various scientific fields, including physics, chemistry, and biology.
Addressing Common Misconceptions
Several misconceptions surround fractions and their manipulation. Let’s clarify some of them:
-
Incorrect Simplification: Students might incorrectly simplify fractions by only dividing the numerator or denominator, without performing the same operation on both. Remember, both the numerator and denominator must be divided by the same common factor.
-
Decimal Approximation: While it's sometimes necessary to approximate a fraction as a decimal for practical purposes, remember that repeating decimals often represent precise values that are lost in approximation.
-
Improper Fractions vs. Mixed Numbers: Both improper fractions and mixed numbers represent the same value; the choice between the two depends on the context and the required form of the answer.
Frequently Asked Questions (FAQ)
Q1: Can I simplify 35/15 by dividing only the numerator by 5?
A1: No. To simplify a fraction, you must divide both the numerator and the denominator by the same common factor. Dividing only the numerator changes the value of the fraction.
Q2: What is the difference between an improper fraction and a mixed number?
A2: An improper fraction has a numerator larger than or equal to its denominator (e.g., 7/3). A mixed number combines a whole number and a proper fraction (e.g., 2 1/3). They represent the same quantity.
Q3: Why is it important to simplify fractions?
A3: Simplifying fractions makes them easier to work with in calculations and comparisons. It also helps to understand the underlying relationships between the numerator and denominator.
Q4: How can I convert a mixed number back into an improper fraction?
A4: To convert a mixed number to an improper fraction, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, 2 1/3 becomes (2 x 3 + 1) / 3 = 7/3.
Conclusion
The seemingly straightforward fraction 35/15 provides a valuable opportunity to explore several fundamental mathematical concepts. Through simplification, decimal conversion, and the understanding of improper fractions and mixed numbers, we gain a deeper appreciation for the versatility and practical application of fractions in various real-world scenarios. Mastering these concepts lays a strong foundation for more advanced mathematical studies and problem-solving. Remember that consistent practice and a clear understanding of the underlying principles are key to confidently working with fractions. Don't hesitate to review these concepts and apply them in diverse contexts to solidify your understanding.
Latest Posts
Latest Posts
-
40 Divided 6
Sep 21, 2025
-
Pc Psu Modular
Sep 21, 2025
-
16 8kg In Stone
Sep 21, 2025
-
3 2 M Cm
Sep 21, 2025
-
36 Of 125
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 35 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.