36 Of 125
interactiveleap
Sep 21, 2025 · 5 min read
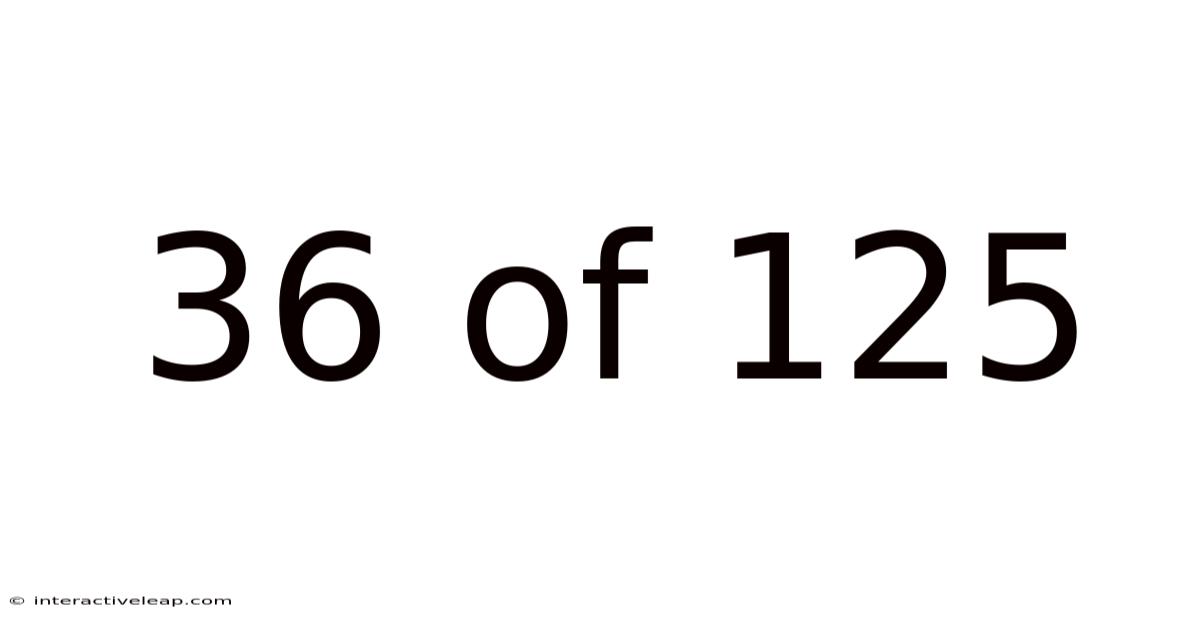
Table of Contents
Decoding the Enigma: 36 of 125 – A Deep Dive into Fraction Simplification and its Applications
The seemingly simple fraction, 36/125, holds within it a world of mathematical concepts, from basic fraction simplification to more advanced applications in various fields. This article will delve into the intricacies of this particular fraction, exploring its simplification, its decimal equivalent, and its significance in understanding fundamental mathematical principles. We will also touch upon practical applications and answer frequently asked questions about fraction simplification. This comprehensive guide will equip you with a deeper understanding of fractions and their role in problem-solving.
Introduction: Understanding Fractions and their Simplification
Fractions represent a part of a whole. They are expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). For example, in the fraction 36/125, 36 is the numerator and 125 is the denominator. Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. This makes the fraction easier to understand and work with. Simplifying fractions is a crucial skill in mathematics and forms the basis for many more complex calculations.
Step-by-Step Simplification of 36/125
The fraction 36/125 is already in its simplest form. To illustrate the process of simplification, let's consider how we'd approach it if it were reducible. The process involves finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
-
Finding the prime factorization: We start by finding the prime factorization of both 36 and 125. The prime factorization of a number is expressing it as a product of its prime factors (numbers divisible only by 1 and themselves).
- 36 = 2 x 2 x 3 x 3 = 2² x 3²
- 125 = 5 x 5 x 5 = 5³
-
Identifying common factors: After finding the prime factorizations, we look for common factors between the numerator and denominator. In this case, there are no common prime factors between 36 (2² x 3²) and 125 (5³).
-
Simplification: Since there are no common factors, the fraction is already in its simplest form. Therefore, 36/125 cannot be simplified further.
Converting 36/125 to a Decimal
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In this case:
36 ÷ 125 = 0.288
Therefore, the decimal equivalent of 36/125 is 0.288. This decimal representation is useful in many practical applications where decimal values are preferred.
The Significance of Understanding Fraction Simplification
The ability to simplify fractions is fundamental to success in mathematics. Here's why:
- Improved clarity: Simplified fractions are easier to understand and interpret than complex fractions. For example, understanding that 1/2 is equivalent to 50/100 makes comparing proportions much simpler.
- Efficiency in calculations: Simplifying fractions before performing other operations, such as addition, subtraction, multiplication, or division, reduces the complexity of the calculations and minimizes errors.
- Foundation for advanced concepts: Fraction simplification is a cornerstone for understanding more advanced mathematical concepts such as ratios, proportions, percentages, and algebraic expressions. A strong grasp of fractions is essential for tackling these more challenging topics.
Applications of Fractions in Real-World Scenarios
Fractions are not merely abstract mathematical concepts; they are essential tools used in numerous real-world applications. Here are a few examples:
- Cooking and baking: Recipes often utilize fractions to specify ingredient quantities, such as ½ cup of sugar or ⅓ teaspoon of salt. Accurate fraction understanding ensures correct measurements.
- Construction and engineering: Precise measurements are critical in construction and engineering, with fractions used extensively in blueprints and design calculations to ensure accuracy and structural integrity.
- Finance and economics: Fractions are fundamental in calculating interest rates, percentages, and shares of ownership in businesses. Accurate fraction calculation is crucial for sound financial management.
- Science and research: Fractions play a significant role in data analysis and scientific measurements. Experiments often involve ratios and proportions, requiring a thorough understanding of fraction manipulation.
Further Exploration: Working with Fractions
While 36/125 is already simplified, let's explore some related concepts to broaden our understanding of fractions:
- Adding and subtracting fractions: To add or subtract fractions, they must have a common denominator. If they don't, you must find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with that common denominator.
- Multiplying fractions: Multiplying fractions is straightforward. Multiply the numerators together and multiply the denominators together. Simplify the resulting fraction if possible.
- Dividing fractions: To divide fractions, invert the second fraction (reciprocal) and multiply. Again, simplify the result if necessary.
Frequently Asked Questions (FAQ)
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with. It also simplifies subsequent calculations, reducing errors and improving efficiency.
Q: What if I cannot find the GCD easily?
A: You can use the Euclidean algorithm to find the GCD of two numbers. This algorithm is a systematic method for finding the greatest common divisor of two integers.
Q: Are there any online tools to simplify fractions?
A: Yes, many online calculators and websites can simplify fractions instantly. These tools are useful for checking your work or for simplifying complex fractions quickly.
Q: How do I convert a decimal to a fraction?
A: To convert a terminating decimal to a fraction, write the decimal as a fraction with a denominator of 10, 100, 1000, etc., depending on the number of decimal places. Then, simplify the fraction to its lowest terms. For repeating decimals, the process is more complex and involves algebraic manipulation.
Conclusion: Mastering the Fundamentals of Fractions
Understanding fractions is a fundamental building block in mathematics and has far-reaching applications in numerous fields. While the fraction 36/125 might seem insignificant in isolation, its analysis underscores the importance of simplification, decimal conversion, and the broader significance of grasping fundamental mathematical principles. Mastering these concepts will not only enhance your mathematical skills but also provide a valuable toolset for tackling a wide array of real-world problems. The ability to confidently work with fractions opens doors to deeper understanding in various academic and professional pursuits. Continue to practice and explore the world of fractions to unlock its full potential.
Latest Posts
Latest Posts
-
2dl En Ml
Sep 21, 2025
-
12 Of 30
Sep 21, 2025
-
Dr John Seward
Sep 21, 2025
-
Wedding Hall Cost
Sep 21, 2025
-
115f To C
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 36 Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.