40 Divided 6
interactiveleap
Sep 21, 2025 · 6 min read
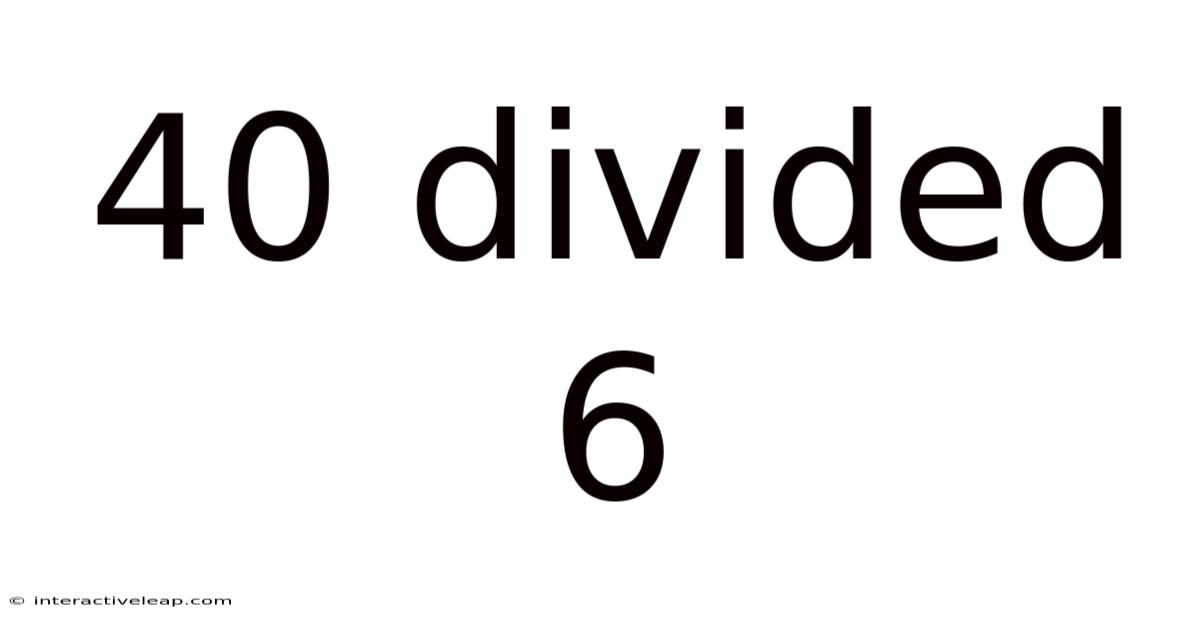
Table of Contents
Unveiling the Mystery: A Deep Dive into 40 Divided by 6
Introduction:
Have you ever wondered what happens when you divide 40 by 6? It's a seemingly simple arithmetic problem, yet it holds a wealth of mathematical concepts that extend far beyond a simple answer. This article will explore the division of 40 by 6 in detail, covering various approaches, interpretations, and applications. We’ll move beyond the basic answer, delving into the concepts of quotients, remainders, fractions, decimals, and real-world applications. Understanding this seemingly simple division problem lays a foundation for more complex mathematical concepts. We'll also explore the related concepts of factors, multiples, and the divisibility rules, showing how they all connect.
The Basic Calculation: Quotient and Remainder
The most straightforward approach to solving 40 divided by 6 is performing long division. This method reveals both the quotient and the remainder.
Let's break down the process:
- Divide: How many times does 6 go into 40? It goes in 6 times (6 x 6 = 36).
- Multiply: Multiply the quotient (6) by the divisor (6): 6 x 6 = 36.
- Subtract: Subtract the product (36) from the dividend (40): 40 - 36 = 4.
- Remainder: The result (4) is the remainder.
Therefore, 40 divided by 6 is 6 with a remainder of 4. This is often expressed as 6 R 4. This simple calculation forms the basis for understanding more complex aspects of this division.
Representing the Result as a Fraction
The remainder isn't the end of the story. We can express the result more precisely using fractions. The remainder (4) becomes the numerator, and the divisor (6) becomes the denominator. This gives us the fraction 4/6.
This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 4 and 6 is 2. Dividing both the numerator and the denominator by 2 simplifies the fraction to 2/3.
Therefore, 40 divided by 6 can also be represented as the mixed number 6 2/3. This represents the whole number quotient (6) and the fractional part (2/3) of the division.
Decimal Representation
Another way to represent the result is using decimals. To convert the fraction 2/3 to a decimal, we perform long division again:
2 ÷ 3 = 0.66666...
This is a repeating decimal, denoted as 0.<u>6</u>. Therefore, 40 divided by 6 can be expressed as 6.666... or 6.<u>6</u>. The repeating decimal nature of the result signifies that the division never ends perfectly, unlike many other divisions with whole number results.
Understanding Factors and Multiples
The concept of factors and multiples provides another perspective on this problem. Factors are numbers that divide evenly into a given number without leaving a remainder. Multiples are numbers obtained by multiplying a given number by any whole number.
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
- Factors of 6: 1, 2, 3, 6
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48...
Notice that 6 is not a factor of 40 because it doesn't divide evenly into 40. The closest multiple of 6 to 40 is 36 (6 x 6), which leaves a remainder of 4. This reinforces the result we obtained through long division.
Divisibility Rules
Divisibility rules are shortcuts to determine if a number is divisible by another number without performing the actual division. While there's no specific divisibility rule for 6 that instantly reveals whether 40 is divisible by 6, we can use the rules for 2 and 3.
- Divisibility rule for 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, 8). 40 is divisible by 2.
- Divisibility rule for 3: A number is divisible by 3 if the sum of its digits is divisible by 3. The sum of the digits in 40 (4 + 0 = 4) is not divisible by 3.
Since 40 is divisible by 2 but not by 3, it's not divisible by 6 (as 6 = 2 x 3). This highlights the interconnectedness of divisibility rules and prime factorization.
Real-World Applications
The division of 40 by 6 has practical applications in various scenarios:
- Sharing resources: Imagine you have 40 candies to share equally among 6 friends. Each friend would get 6 candies, and you'd have 4 candies left over.
- Measurement and conversions: Consider converting 40 inches into feet. Since there are 12 inches in a foot, the calculation would involve dividing 40 by 12 (not 6 in this case), illustrating the concept in a measurement context.
- Proportions and ratios: If a recipe calls for 6 parts of ingredient A and you have 40 parts of total ingredients, the proportion of ingredient A would be represented by 40/6, which simplifies to 20/3 or 6 2/3.
These examples show how the concept of dividing 40 by 6, with its quotient and remainder, has real-world relevance beyond abstract mathematical exercises.
Exploring Further: Prime Factorization
The prime factorization of a number is expressing it as a product of its prime factors (numbers divisible only by 1 and themselves). This can offer further insight into divisibility.
- Prime factorization of 40: 2 x 2 x 2 x 5 = 2³ x 5
- Prime factorization of 6: 2 x 3
Because the prime factorization of 6 includes a 3, and the prime factorization of 40 does not, this again confirms that 40 is not divisible by 6.
Conclusion:
The seemingly simple problem of 40 divided by 6 unfolds into a rich exploration of various mathematical concepts. From the basic quotient and remainder to the representation as a fraction and decimal, the problem demonstrates the interplay between whole numbers, fractions, and decimals. Furthermore, exploring factors, multiples, divisibility rules, and prime factorization provides deeper insights into the nature of numbers and their relationships. This comprehensive analysis shows that even a basic arithmetic problem can offer a pathway to a deeper understanding of mathematical principles and their applications in the real world. The seemingly simple answer hides a wealth of mathematical knowledge waiting to be discovered.
Frequently Asked Questions (FAQ):
-
Q: What is the exact decimal value of 40/6? A: There is no exact decimal value, as it's a repeating decimal: 6.666... or 6.<u>6</u>.
-
Q: Can I use a calculator to solve this? A: Yes, a calculator will give you the decimal representation (6.666...). However, understanding the long division process and the concept of the remainder is crucial for a complete understanding.
-
Q: Why is the remainder important? A: The remainder provides crucial information when dealing with real-world problems involving discrete quantities (like sharing candies) or when the result needs to be expressed as a fraction or mixed number.
-
Q: Are there other ways to solve this problem besides long division? A: While long division is the most common method, you can also use other methods such as repeated subtraction or visual models (like dividing objects into groups). However, long division offers the most efficient and direct approach.
-
Q: How does this relate to more advanced mathematics? A: Understanding division, remainders, and fractions forms the foundation for more advanced concepts like modular arithmetic, algebra, and calculus. The ability to handle these basic concepts is essential for success in higher-level mathematics.
Latest Posts
Latest Posts
-
1 5 In Decimal
Sep 21, 2025
-
0 1 Into Fraction
Sep 21, 2025
-
Pus Cow Milk
Sep 21, 2025
-
2dl En Ml
Sep 21, 2025
-
12 Of 30
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 40 Divided 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.