55 Of 20
interactiveleap
Sep 21, 2025 · 5 min read
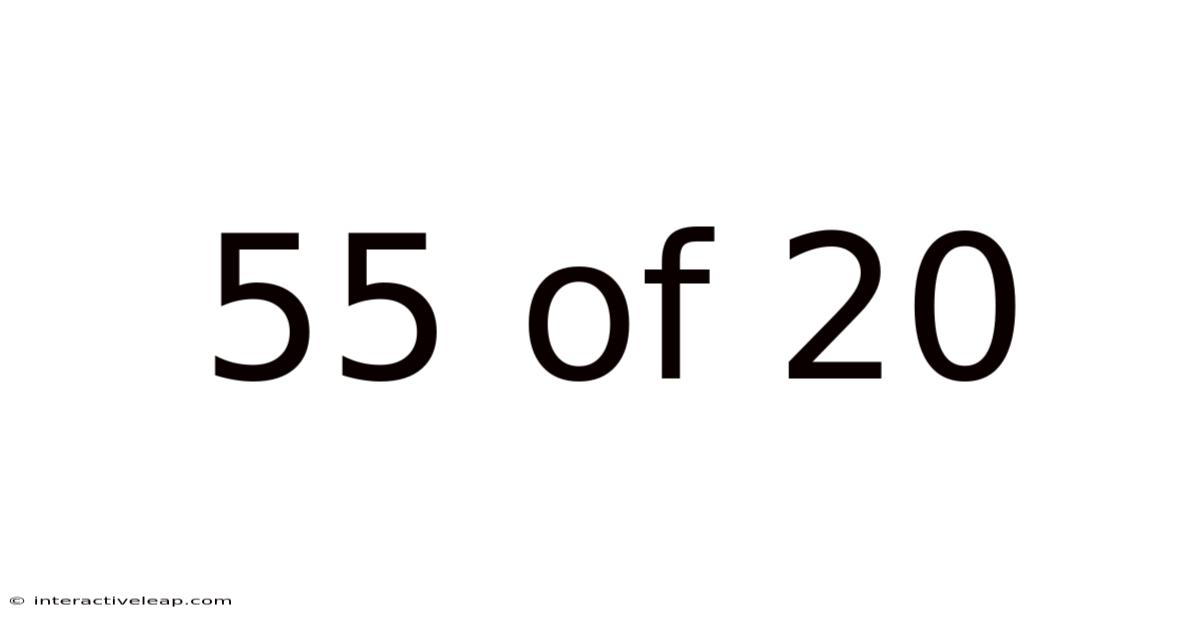
Table of Contents
Decoding the Fraction 55/20: A Comprehensive Guide
Understanding fractions is fundamental to mathematics, and mastering them unlocks a world of problem-solving abilities. This article delves deep into the fraction 55/20, exploring its simplification, conversion to decimals and percentages, real-world applications, and related concepts. Whether you're a student struggling with fractions or an adult looking to refresh your math skills, this guide provides a comprehensive and engaging exploration of 55/20.
Introduction: What is 55/20?
The fraction 55/20 represents the ratio of 55 to 20. It signifies that we have 55 parts out of a possible 20 parts. This immediately suggests that the fraction is improper, meaning the numerator (55) is larger than the denominator (20). Improper fractions are often more readily understood when converted into mixed numbers or decimals. This article will guide you through these conversions and more. We'll cover simplifying the fraction, finding its decimal equivalent, expressing it as a percentage, and finally, exploring some real-world scenarios where understanding 55/20 becomes crucial.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before converting 55/20 to other forms, it's crucial to simplify it. Simplifying a fraction means reducing it to its lowest terms. This is achieved by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both 55 and 20 without leaving a remainder.
Let's find the GCD of 55 and 20 using the prime factorization method:
- Prime factorization of 55: 5 x 11
- Prime factorization of 20: 2 x 2 x 5
The only common prime factor is 5. Therefore, the GCD of 55 and 20 is 5.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
55 ÷ 5 = 11 20 ÷ 5 = 4
Therefore, the simplified form of 55/20 is 11/4.
Converting to a Mixed Number
An improper fraction like 11/4 can be converted into a mixed number, which combines a whole number and a proper fraction. To do this, we perform division:
11 ÷ 4 = 2 with a remainder of 3.
This means that 11/4 is equivalent to 2 ¾. This representation is often easier to visualize and understand in practical applications.
Converting to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. We can use either the simplified fraction (11/4) or the original fraction (55/20):
- Using 11/4: 11 ÷ 4 = 2.75
- Using 55/20: 55 ÷ 20 = 2.75
In both cases, the decimal equivalent of 55/20 is 2.75.
Converting to a Percentage
To convert a decimal to a percentage, we multiply by 100 and add the percent sign (%).
2.75 x 100% = 275%
This indicates that 55/20 represents 275% of a whole. This might seem counterintuitive at first, as percentages are usually less than or equal to 100%, but remember that 55/20 is an improper fraction, representing more than one whole.
Real-World Applications of 55/20
Understanding fractions like 55/20 is crucial in various real-world scenarios:
-
Measurement and Proportion: Imagine you're measuring ingredients for a recipe. If a recipe calls for 20 ounces of flour and you have 55 ounces, you have 55/20 or 275% of the required amount. This understanding allows you to adjust other ingredients proportionally.
-
Finance and Budgeting: If you budgeted $20 for transportation and spent $55, you have exceeded your budget by 55/20 or 275% – a clear indication of overspending.
-
Data Analysis: In statistical analysis, fractions are often used to represent proportions or ratios within datasets. For instance, if 55 out of 20 surveyed individuals prefer a certain product, the fraction 55/20 represents a significant preference.
-
Construction and Engineering: Precise measurements are paramount in construction and engineering. Understanding and manipulating fractions is essential for accurate calculations and avoiding errors.
Further Exploration: Working with Fractions
Understanding 55/20 provides a solid foundation for working with more complex fractions. Here are some related concepts to explore:
-
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. For instance, adding 55/20 and another fraction would require finding a common denominator before performing the operation.
-
Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators together and the denominators together. Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying.
-
Equivalent Fractions: Equivalent fractions represent the same value but have different numerators and denominators. For instance, 55/20, 11/4, and 2.75 are all equivalent representations.
-
Comparing Fractions: To compare fractions, find a common denominator and compare the numerators. The fraction with the larger numerator is the larger fraction.
-
Fractions and Decimals: The seamless conversion between fractions and decimals is a fundamental skill in mathematics and real-world problem-solving.
Frequently Asked Questions (FAQ)
Q: Why is simplifying a fraction important?
A: Simplifying a fraction makes it easier to understand and work with. It reduces the numbers to their smallest possible values, avoiding unnecessary complexity in calculations.
Q: Can I convert any fraction to a decimal?
A: Yes, any fraction can be converted to a decimal by dividing the numerator by the denominator.
Q: What does it mean when a percentage is greater than 100%?
A: A percentage greater than 100% indicates that the value exceeds the whole. In the case of 55/20 (275%), it represents 2.75 times the whole.
Q: Are there any other methods to find the GCD besides prime factorization?
A: Yes, the Euclidean algorithm is another efficient method for finding the greatest common divisor of two numbers.
Conclusion: Mastering Fractions – A Stepping Stone to Success
Mastering fractions, even complex ones like 55/20, is crucial for success in mathematics and numerous real-world applications. By understanding the steps involved in simplification, conversion to decimals and percentages, and the practical applications, you can build a solid foundation for more advanced mathematical concepts. Remember, the key is practice. The more you work with fractions, the more comfortable and confident you will become in manipulating and understanding them. This thorough understanding will undoubtedly enhance your problem-solving skills and open doors to further mathematical exploration.
Latest Posts
Latest Posts
-
140gms In Ounces
Sep 21, 2025
-
50 Of 40
Sep 21, 2025
-
Beatles Monopoly Board
Sep 21, 2025
-
Opposite Of Diligent
Sep 21, 2025
-
1 8 As Fraction
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 55 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.