18 5 6
interactiveleap
Sep 21, 2025 · 6 min read
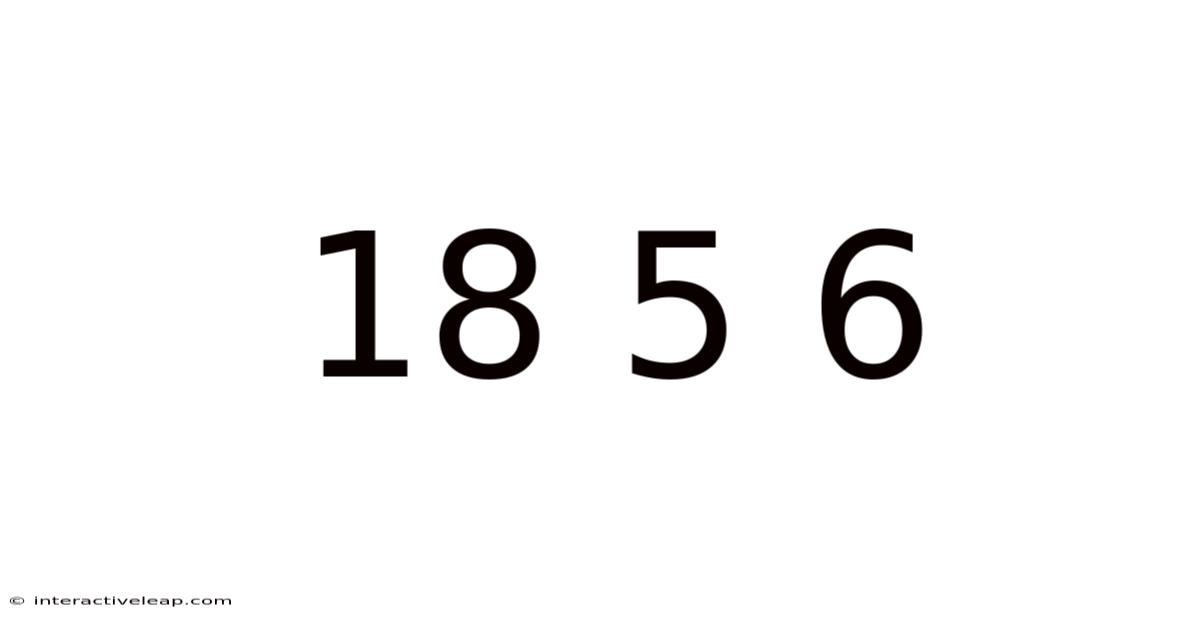
Table of Contents
Decoding 18, 5, and 6: A Journey Through Number Theory, Combinatorics, and Geometry
The seemingly simple sequence "18, 5, 6" might not initially scream "exciting mathematical exploration," but a closer look reveals a wealth of connections spanning various branches of mathematics. This article delves into the fascinating relationships between these three numbers, exploring their properties within number theory, combinatorics, and even hinting at geometric interpretations. We will move beyond simple arithmetic and uncover deeper mathematical structures and concepts. This journey will be accessible to those with a basic mathematical background, providing both foundational knowledge and stimulating explorations for those with more advanced understanding.
I. Number Theory Perspectives: Divisibility, Factors, and Prime Factorization
Let's begin with the foundational branch of mathematics: number theory. Each number—18, 5, and 6—holds unique properties concerning divisibility and factors.
-
18: This is a composite number, meaning it's divisible by numbers other than 1 and itself. Its factors are 1, 2, 3, 6, 9, and 18. Its prime factorization is 2 x 3². Notice the presence of both 2 and 3 as prime factors – this will become relevant later.
-
5: This is a prime number, meaning its only divisors are 1 and itself. This is a fundamental property in number theory, distinguishing it from composite numbers.
-
6: Another composite number, its factors include 1, 2, 3, and 6. Its prime factorization is 2 x 3. Observe that it shares prime factors with 18.
The interplay between the prime factorizations of 18 and 6 is noteworthy. They both contain the prime factors 2 and 3. This shared factorization hints at potential relationships in other mathematical contexts, as we shall see. The fact that 5 is a prime number, distinct from the prime factors of 18 and 6, sets it apart and adds another layer of complexity to any analysis that includes all three numbers.
Greatest Common Divisor (GCD) and Least Common Multiple (LCM): Analyzing the GCD and LCM of these numbers provides further insights. The GCD of 18 and 6 is 6, indicating that 6 is the largest number that divides both 18 and 6. The LCM of 18 and 6 is 18, signifying the smallest number that is a multiple of both 18 and 6. Including 5 in these calculations would yield a GCD of 1 (as 5 shares no common factors with 18 or 6) and an LCM of 18 x 5 = 90.
II. Combinatorics: Exploring Permutations and Combinations
The numbers 18, 5, and 6 can be explored through the lens of combinatorics, which deals with counting and arrangements.
-
Permutations: If we consider these numbers as distinct objects, the number of permutations (arrangements) of these three numbers is 3! (3 factorial) = 3 x 2 x 1 = 6. This means there are six distinct ways to arrange the numbers 18, 5, and 6.
-
Combinations: If we are interested in selecting subsets of these numbers, the combinations are as follows:
- We can choose one number in 3 ways (18, 5, or 6).
- We can choose two numbers in 3 ways (18 & 5, 18 & 6, or 5 & 6).
- We can choose all three numbers in 1 way.
This simple example demonstrates the basic principles of combinatorics. Imagine extending this to larger sets of numbers or considering more complex selection criteria – the field rapidly expands into intricate and powerful mathematical tools used in probability, statistics, and computer science.
III. Geometric Interpretations: A Glimpse into Geometry
While less direct, the numbers 18, 5, and 6 can spark geometric inquiries.
-
Area and Perimeter: We can consider these numbers as representing lengths or areas. For example, 6 could represent the side length of a square (area = 36), while 18 could represent its perimeter. Exploring the relationship between area and perimeter using different geometric shapes creates interesting problems.
-
Volume: Extending to three dimensions, these numbers could be related to the dimensions of a rectangular prism. Finding the volume and surface area with different combinations of these numbers provides a geometric context.
-
Angles: While less obvious, the numbers could represent angles in degrees or radians, opening up possibilities within trigonometry and geometric constructions.
IV. Advanced Mathematical Concepts: A Hint of Deeper Connections
Moving beyond basic arithmetic and geometry, we can hint at deeper mathematical connections.
-
Modular Arithmetic: The numbers 18, 5, and 6 can be used in modular arithmetic. For example, considering these numbers modulo 3 (the remainder when divided by 3), we have 18 ≡ 0 (mod 3), 5 ≡ 2 (mod 3), and 6 ≡ 0 (mod 3). This reveals a relationship based on divisibility by 3. Exploring modulo operations with other numbers reveals further patterns.
-
Number Bases: We can represent these numbers in different bases (like binary, ternary, etc.). This highlights the concept of representing numbers in various systems and the inherent flexibility of numerical representation.
-
Abstract Algebra: Although beyond the scope of this introductory exploration, these numbers could find connections within abstract algebra through the concept of groups, rings, and fields. These structures define abstract mathematical objects and their operations, providing frameworks for analyzing number systems beyond the familiar integers.
V. Expanding the Exploration: Further Investigations
This article has only scratched the surface of the mathematical richness embedded within the seemingly simple sequence "18, 5, 6." Numerous avenues for further exploration exist:
-
Diophantine Equations: Creating and solving Diophantine equations (equations where solutions are restricted to integers) involving these numbers can lead to challenging and rewarding mathematical puzzles.
-
Continued Fractions: Expressing these numbers as continued fractions can unveil relationships based on rational approximations and infinite series.
-
Number Patterns and Sequences: Investigating whether these numbers belong to or generate interesting number patterns and sequences can lead to the discovery of new mathematical relationships.
VI. Conclusion: The Unfolding Beauty of Mathematics
The exploration of the numbers 18, 5, and 6 demonstrates the interconnectedness of different mathematical branches. Starting with simple observations about divisibility and factors, we ventured into combinatorics, geometry, and hinted at advanced concepts in abstract algebra. The seemingly mundane sequence becomes a gateway to a rich and rewarding mathematical landscape. The beauty of mathematics lies in its ability to connect seemingly disparate concepts, revealing deeper structures and patterns that enrich our understanding of the world around us. The exploration never truly ends; every question answered sparks a multitude of new questions, inviting further inquiry and expanding our mathematical horizons. The journey of mathematical discovery is a continuous process of exploration, revealing the elegance and profound interconnectedness within the seemingly simple. Remember that the power of mathematical thinking lies not just in finding answers but in asking the right questions. So, continue exploring – the mathematical universe awaits!
Latest Posts
Latest Posts
-
16 8kg In Stone
Sep 21, 2025
-
3 2 M Cm
Sep 21, 2025
-
36 Of 125
Sep 21, 2025
-
140gms In Ounces
Sep 21, 2025
-
50 Of 40
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 18 5 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.