X 3x 2
interactiveleap
Sep 16, 2025 · 6 min read
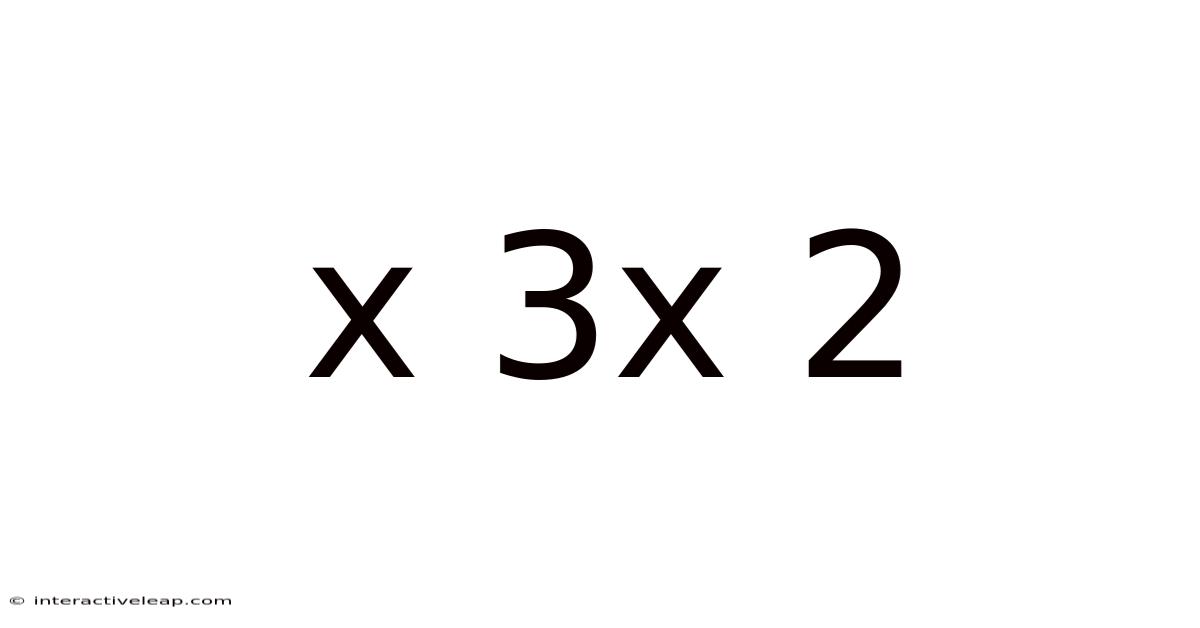
Table of Contents
Decoding x³ - 3x²: A Deep Dive into Cubic Functions and Their Applications
This article explores the cubic function x³ - 3x², delving into its properties, graphing techniques, applications, and real-world relevance. Understanding this seemingly simple function unveils fundamental concepts within algebra, calculus, and beyond. We'll cover everything from basic factorization to advanced calculus concepts, ensuring a comprehensive understanding for learners of all levels. Prepare to unlock the secrets hidden within this intriguing cubic expression!
Understanding the Basics: Factorization and Roots
The cubic function f(x) = x³ - 3x² can be factored to reveal crucial insights. The most apparent common factor is x². Factoring this out, we get:
f(x) = x²(x - 3)
This factored form immediately reveals the roots (or zeros) of the function. A root is a value of x for which f(x) = 0. In this case, we have two roots:
- x = 0: This is a root of multiplicity 2, meaning the graph touches the x-axis at x = 0 but doesn't cross it.
- x = 3: This is a root of multiplicity 1, meaning the graph crosses the x-axis at x = 3.
Understanding the multiplicity of roots is vital for sketching the graph accurately.
Graphing the Function: Visualizing the Cubic Curve
Now that we've identified the roots, let's consider how to graph f(x) = x³ - 3x².
-
x-intercepts: As determined above, the x-intercepts are at x = 0 and x = 3.
-
y-intercept: To find the y-intercept, we set x = 0. This gives us f(0) = 0³ - 3(0)² = 0. Therefore, the y-intercept is at (0, 0).
-
Behavior at Infinity: As x approaches positive infinity (x → ∞), f(x) also approaches positive infinity (f(x) → ∞). Conversely, as x approaches negative infinity (x → -∞), f(x) approaches negative infinity (f(x) → -∞). This indicates the overall trend of the cubic function.
-
Critical Points: To find the critical points (local maxima and minima), we need to find the first derivative and set it equal to zero. The first derivative is:
f'(x) = 3x² - 6x
Setting f'(x) = 0, we get:
3x² - 6x = 0 3x(x - 2) = 0
This gives us two critical points: x = 0 and x = 2.
- Second Derivative Test: To determine whether these critical points are maxima or minima, we use the second derivative:
f''(x) = 6x - 6
- At x = 0, f''(0) = -6, indicating a local maximum.
- At x = 2, f''(2) = 6, indicating a local minimum.
By considering these points and the overall behavior of the function, we can sketch a reasonably accurate graph. The graph will have a local maximum at (0,0) and a local minimum at (2,-4). It will pass through the x-axis at x=0 and x=3.
Exploring the Function's Properties: Concavity and Inflection Points
The second derivative, f''(x) = 6x - 6, also helps us understand the concavity of the function. The function is concave down where f''(x) < 0 and concave up where f''(x) > 0.
- f''(x) < 0 when 6x - 6 < 0, which simplifies to x < 1. Therefore, the function is concave down for x < 1.
- f''(x) > 0 when 6x - 6 > 0, which simplifies to x > 1. Therefore, the function is concave up for x > 1.
The inflection point occurs where the concavity changes. In this case, the inflection point is at x = 1. We can find the y-coordinate by substituting x = 1 into the original function: f(1) = 1³ - 3(1)² = -2. Thus, the inflection point is (1, -2).
Applications in Real-World Scenarios
Cubic functions, while seemingly abstract, have numerous real-world applications:
-
Modeling Physical Phenomena: Cubic functions can model various physical phenomena, such as the trajectory of a projectile under the influence of gravity (taking air resistance into account). The height of the projectile over time could be represented by a cubic equation.
-
Engineering and Design: Cubic curves are used in engineering design, particularly in creating smooth, aesthetically pleasing curves for structures like bridges and architectural elements.
-
Economics and Business: Cubic functions can be used to model cost functions, revenue functions, or profit functions in business scenarios. The optimal production level might be determined by finding the minimum or maximum of a cubic function representing profit.
-
Data Analysis and Curve Fitting: Cubic functions, like other polynomial functions, can be used to fit data points to create a smooth curve representing trends or relationships. This is useful in various fields, from statistics to scientific research.
-
Computer Graphics and Animation: Cubic curves, such as Bézier curves, are fundamental in computer graphics and animation for creating smooth and realistic curves for shapes, character movements, and camera paths.
Advanced Concepts: Calculus and Beyond
Let's explore some more advanced concepts related to x³ - 3x²:
- Integration: The definite integral of x³ - 3x² provides the area under the curve between two specified points. The indefinite integral (antiderivative) is:
∫(x³ - 3x²)dx = (1/4)x⁴ - x³ + C, where C is the constant of integration.
-
Derivatives and Optimization: As shown earlier, the first and second derivatives are crucial for finding critical points (maxima and minima) and inflection points. These are essential in optimization problems, such as finding the maximum profit or minimum cost in business applications.
-
Taylor and Maclaurin Series: More advanced calculus techniques, such as Taylor and Maclaurin series, can be used to approximate the function x³ - 3x² using an infinite sum of terms. This can be useful for numerical calculations or approximations.
Frequently Asked Questions (FAQ)
Q: What is the domain of the function x³ - 3x²?
A: The domain of a polynomial function is all real numbers (-∞, ∞).
Q: How many turning points does the function have?
A: The function has two turning points: a local maximum and a local minimum.
Q: Can this function be expressed in different forms?
A: Yes, while the factored form x²(x-3) is useful for finding roots, the expanded form x³ - 3x² is also important. Other forms, such as a Taylor series expansion, are possible but are typically used in more advanced mathematical contexts.
Q: What are the applications of the derivative of this function?
A: The derivative helps determine the slope of the tangent line at any point on the curve and is crucial for finding critical points (maxima and minima) used in optimization problems.
Conclusion: Unlocking the Power of Cubic Functions
The seemingly simple cubic function x³ - 3x² offers a rich tapestry of mathematical concepts, from basic factorization and graphing to advanced calculus techniques and real-world applications. By understanding its roots, critical points, concavity, and behavior at infinity, we can gain a deep appreciation of its properties and its role in modeling various phenomena. This comprehensive exploration provides a foundation for tackling more complex cubic functions and other polynomial expressions, paving the way for further exploration in higher-level mathematics and related fields. Remember, the key to mastering mathematics lies in understanding the fundamentals and applying them to real-world problems. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
Wishes Were Horses
Sep 16, 2025
-
21 Of 230
Sep 16, 2025
-
87 9kg In Stone
Sep 16, 2025
-
4000 60
Sep 16, 2025
-
5000 X 50
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 3x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.