4000 / 60
interactiveleap
Sep 16, 2025 · 6 min read
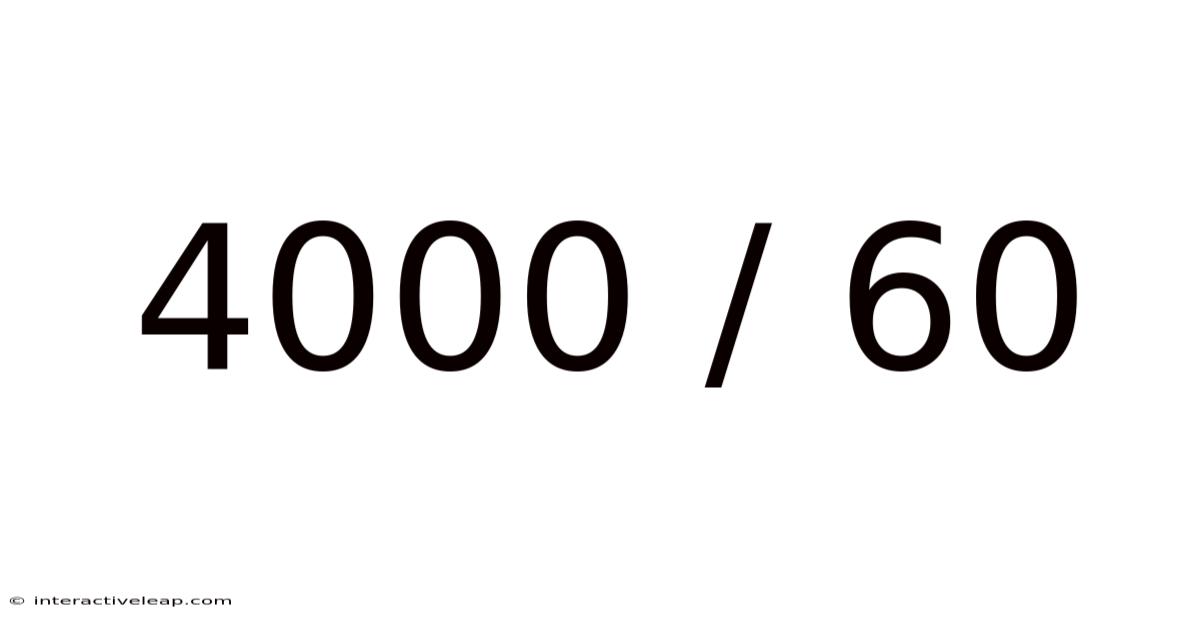
Table of Contents
Decoding 4000/60: Understanding Ratios, Fractions, and Their Applications
The expression "4000/60" might seem intimidating at first glance, but it's simply a ratio or fraction representing a relationship between two numbers. This article will explore the meaning of 4000/60, delve into the process of simplifying fractions, discuss its practical applications, and address frequently asked questions. Understanding ratios and fractions is crucial for various fields, from basic mathematics to advanced engineering and finance. Let's break it down.
Introduction: What Does 4000/60 Represent?
4000/60 represents a ratio of 4000 to 60. In simpler terms, it's a fraction where 4000 is the numerator (the top number) and 60 is the denominator (the bottom number). This ratio can be interpreted in various contexts: it could represent the relationship between a total amount and a smaller part, a rate, or a proportion. For example, it could describe the number of items produced versus the time taken, the number of successful attempts versus total attempts, or even the comparison between two different quantities. The key is understanding the context in which this ratio is used to interpret its meaning accurately.
Simplifying the Fraction: Finding the Simplest Form
Before delving into applications, it's crucial to simplify the fraction 4000/60. Simplifying a fraction means reducing it to its lowest terms – expressing it with the smallest possible whole numbers while retaining its value. We achieve this by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
The GCD of 4000 and 60 can be found using various methods, including prime factorization or the Euclidean algorithm. Let’s use prime factorization:
- Prime factorization of 4000: 2⁵ × 5³
- Prime factorization of 60: 2² × 3 × 5
The common factors are 2² and 5. Therefore, the GCD is 2² × 5 = 20.
Now, we divide both the numerator and denominator by 20:
4000 ÷ 20 = 200 60 ÷ 20 = 3
Therefore, the simplified fraction is 200/3. This is the simplest form of 4000/60, representing the same ratio but in a more manageable format.
Converting to Decimal and Percentage: Different Representations
While the fraction 200/3 is useful, converting it to a decimal or a percentage can offer additional clarity and ease of comparison.
To convert the fraction to a decimal, we perform the division:
200 ÷ 3 ≈ 66.67
Therefore, 4000/60 is approximately 66.67 as a decimal.
To express it as a percentage, we multiply the decimal by 100:
66.67 × 100 = 66.67%
These different representations – fraction, decimal, and percentage – provide flexible ways to understand and utilize the ratio. The best representation depends on the specific context and the intended use.
Practical Applications: Real-World Scenarios
The ratio 4000/60, or its simplified form 200/3, finds applications in numerous real-world situations:
-
Production Rate: Imagine a factory producing 4000 units in 60 hours. The ratio 4000/60 represents the production rate – approximately 66.67 units per hour. This information is critical for production planning, resource allocation, and performance evaluation.
-
Success Rate: If 4000 out of 60 attempts are successful, the ratio indicates a success rate of approximately 66.67%. This is valuable in various contexts, such as analyzing the effectiveness of a marketing campaign, assessing the accuracy of a test, or determining the reliability of a system.
-
Financial Ratios: In finance, ratios are extensively used to analyze a company's performance. For example, the ratio could represent the relationship between revenue and expenses, or assets and liabilities. Understanding these ratios is critical for making informed financial decisions.
-
Engineering and Physics: Ratios play a crucial role in many engineering and physics calculations, such as determining the scale of a model, calculating the strength of materials, or analyzing the efficiency of a system. The ratio 4000/60 might represent the relationship between different physical quantities.
-
Recipe Scaling: Even in everyday cooking, ratios are essential. If a recipe calls for a specific ratio of ingredients, understanding how to scale that ratio up or down is crucial for adjusting the recipe to serve more or fewer people.
Further Exploration: Proportions and Similar Triangles
Understanding the ratio 4000/60 extends beyond simple calculations. It forms the basis of concepts like proportions and similar triangles. A proportion is an equation stating that two ratios are equal. For example, if we have another ratio, say x/y, and it's proportional to 4000/60, we can set up a proportion:
x/y = 4000/60 = 200/3
This allows us to solve for x or y if we know the value of the other variable. This concept is heavily used in various problem-solving scenarios.
Similarly, in geometry, the concept of similar triangles relies on proportional relationships between corresponding sides. If two triangles are similar, the ratios of their corresponding sides are equal. This property is essential for solving problems involving scale drawings, mapmaking, and other geometric applications.
Frequently Asked Questions (FAQ)
Q1: What is the simplest way to simplify 4000/60?
A1: The simplest way is to find the greatest common divisor (GCD) of 4000 and 60, which is 20. Dividing both the numerator and denominator by 20 gives the simplified fraction 200/3.
Q2: Can 200/3 be converted to a mixed number?
A2: Yes, 200/3 can be expressed as a mixed number. Performing the division, we get 66 with a remainder of 2. Therefore, the mixed number representation is 66 ⅔.
Q3: What are some real-world examples where this type of ratio is used?
A3: Real-world examples include calculating production rates, determining success rates, analyzing financial ratios, solving engineering problems, and scaling recipes.
Q4: How do I solve problems involving proportions using this ratio?
A4: Set up a proportion by equating the given ratio (4000/60 or 200/3) with another ratio containing an unknown variable. Then, cross-multiply and solve for the unknown variable.
Q5: Why is simplifying a fraction important?
A5: Simplifying a fraction makes it easier to understand, compare, and use in calculations. It represents the same ratio in a more concise and manageable form.
Conclusion: Mastering Ratios and Fractions
The seemingly simple ratio 4000/60 opens doors to a vast world of mathematical concepts and real-world applications. Understanding how to simplify fractions, convert them to decimals and percentages, and apply them to solve problems is crucial for success in various fields. This exploration of 4000/60 provides a foundational understanding of ratios and fractions, empowering you to tackle more complex mathematical challenges with confidence. Remember that mastering these fundamental concepts lays the groundwork for more advanced mathematical studies and problem-solving skills across diverse disciplines.
Latest Posts
Latest Posts
-
William Grant Composer
Sep 16, 2025
-
15 Of 22
Sep 16, 2025
-
Jello Swimming Pool
Sep 16, 2025
-
Collective Noun Bear
Sep 16, 2025
-
47 1kg In Stone
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 4000 / 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.