5000 X 50
interactiveleap
Sep 16, 2025 · 5 min read
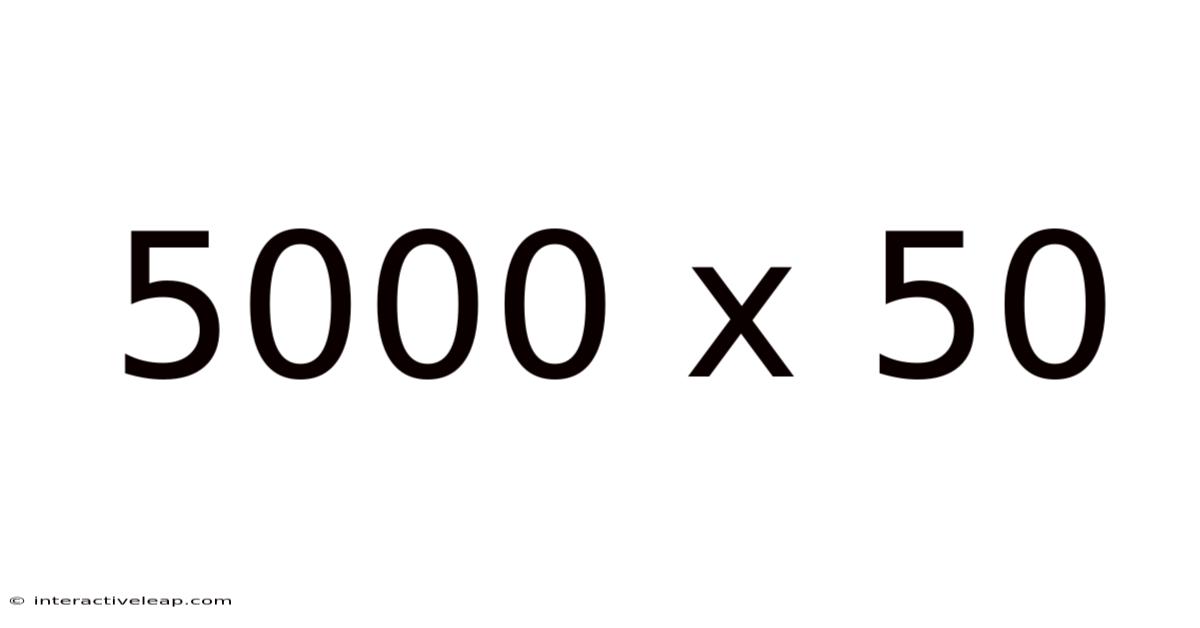
Table of Contents
Decoding 5000 x 50: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem 5000 x 50, delving far beyond the immediate answer to uncover the underlying mathematical principles, practical applications, and broader implications of this calculation. We’ll examine different methods of solving this problem, discuss its relevance in various fields, and address common misconceptions surrounding multiplication. This comprehensive guide will be beneficial for students, educators, and anyone interested in a deeper understanding of arithmetic and its real-world relevance.
I. Understanding the Basics: Multiplication as Repeated Addition
At its core, multiplication is a shortcut for repeated addition. 5000 x 50 means adding 5000 to itself 50 times. While this approach is feasible for smaller numbers, it becomes incredibly time-consuming for larger values like this. This is where the efficiency of multiplication shines. The problem 5000 x 50 represents a fundamental concept in mathematics, forming the basis for more complex calculations and applications across numerous disciplines.
II. Methods for Solving 5000 x 50
Several approaches can efficiently solve 5000 x 50:
-
Standard Multiplication: This involves the traditional method taught in schools, using place value and carrying over digits. We can break it down as follows:
5000 x 50 ------- 0000 (5000 x 0) 250000 (5000 x 5) ------- 250000 -
Distributive Property: This property allows us to break down the multiplication into smaller, more manageable parts. We can rewrite 50 as (5 x 10) and then distribute:
5000 x (5 x 10) = (5000 x 5) x 10 = 25000 x 10 = 250000
-
Mental Math Techniques: With practice, we can perform this calculation mentally. Recognizing that 50 is half of 100 simplifies the process:
5000 x 50 = 5000 x (100/2) = (5000 x 100) / 2 = 500000 / 2 = 250000
-
Using Scientific Notation: For very large or very small numbers, scientific notation streamlines calculations. We can rewrite 5000 as 5 x 10³ and 50 as 5 x 10¹. Then:
(5 x 10³) x (5 x 10¹) = 25 x 10⁴ = 250000
III. The Significance of Place Value
Understanding place value is crucial for accurately performing multiplication, especially with larger numbers. In 5000, each digit represents a different power of 10:
- 5 represents 5 thousands (5 x 1000)
- 0 represents 0 hundreds (0 x 100)
- 0 represents 0 tens (0 x 10)
- 0 represents 0 ones (0 x 1)
Similarly, in 50, we have:
- 5 represents 5 tens (5 x 10)
- 0 represents 0 ones (0 x 1)
The correct placement of digits during the multiplication process ensures the accurate representation of the final product.
IV. Real-World Applications of 5000 x 50 (and its Principles)
While 5000 x 50 might seem abstract, its underlying principles are constantly applied in numerous real-world scenarios:
- Business and Finance: Calculating total revenue from selling 5000 units of a product at $50 each.
- Engineering and Construction: Determining the total area of a rectangular plot of land measuring 5000 meters by 50 meters.
- Data Analysis: Calculating the total number of items based on 50 groups of 5000 items each.
- Scientific Calculations: Many scientific formulas involve multiplication, often with much larger numbers than 5000 x 50. The fundamental principles remain the same.
- Everyday Life: Even simple tasks like calculating the total cost of 50 items at $50 each utilize the same multiplication concepts.
V. Extending the Concept: Exploring Larger Multiplications
The principles involved in solving 5000 x 50 can be readily extended to more complex multiplications. Consider the following examples:
- 5000 x 500: This expands the problem, requiring a deeper understanding of place value and multiplication. The solution follows the same principles, resulting in 2,500,000.
- 5000 x 5000: This example further highlights the significance of place value and the efficiency of different multiplication methods. The answer is 25,000,000.
- Multiplying by multiples of 10: Understanding that multiplying by 10, 100, or 1000 simply involves adding zeros is a crucial skill for efficient calculation.
VI. Addressing Common Misconceptions
Several common errors can occur when performing multiplication, especially with larger numbers:
- Incorrect Place Value: Failing to align digits correctly during the multiplication process leads to inaccurate results.
- Errors in Carrying Over: Incorrectly carrying over digits from one column to the next can significantly alter the final answer.
- Misunderstanding Zeroes: Not understanding the role of zeroes in place value can cause significant errors, especially in multiplications involving multiples of 10.
VII. The Importance of Practice and Understanding
Mastering multiplication isn't just about memorizing multiplication tables; it's about understanding the underlying principles and applying them to various situations. Consistent practice, utilizing different methods, and actively seeking to understand the "why" behind each step are key to building proficiency.
VIII. Connecting Multiplication to Other Mathematical Concepts
Multiplication is intimately connected to other core mathematical concepts:
- Division: Division is the inverse operation of multiplication. Understanding this relationship is crucial for solving a wide range of problems. For example, 250000 / 50 = 5000.
- Exponents: Repeated multiplication can be expressed using exponents. For example, 10 x 10 x 10 can be written as 10³.
- Algebra: Multiplication forms the basis of many algebraic expressions and equations.
IX. Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to solve 5000 x 50?
A: The easiest method depends on individual preference and familiarity. The distributive property (5000 x 5 x 10) or mental math (halving 500000) are often efficient.
-
Q: Why is it important to learn multiplication?
A: Multiplication is a fundamental building block for higher-level mathematics and is crucial for solving problems in various fields, from finance to science.
-
Q: Are there any online resources to help me practice multiplication?
A: Numerous online platforms and educational websites offer interactive exercises and tutorials to practice multiplication skills.
-
Q: What if I make a mistake during multiplication?
A: Carefully review your steps, focusing on place value and carrying over. Using alternative methods to verify your answer can be beneficial.
X. Conclusion: Beyond the Numbers
Solving 5000 x 50 delivers more than just a numerical answer (250,000); it provides a gateway to understanding fundamental mathematical principles applicable across numerous disciplines and everyday situations. The seemingly simple calculation opens doors to a deeper comprehension of arithmetic, emphasizing the importance of place value, the efficiency of various calculation methods, and the power of mathematical thinking in solving real-world problems. Mastering these principles empowers us not only to solve mathematical problems but to approach challenges in various aspects of life with greater clarity and efficiency. By understanding the "why" behind the calculation, we unlock a deeper appreciation for the elegance and utility of mathematics.
Latest Posts
Latest Posts
-
William Grant Composer
Sep 16, 2025
-
15 Of 22
Sep 16, 2025
-
Jello Swimming Pool
Sep 16, 2025
-
Collective Noun Bear
Sep 16, 2025
-
47 1kg In Stone
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 5000 X 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.