88 X 4
interactiveleap
Sep 13, 2025 · 6 min read
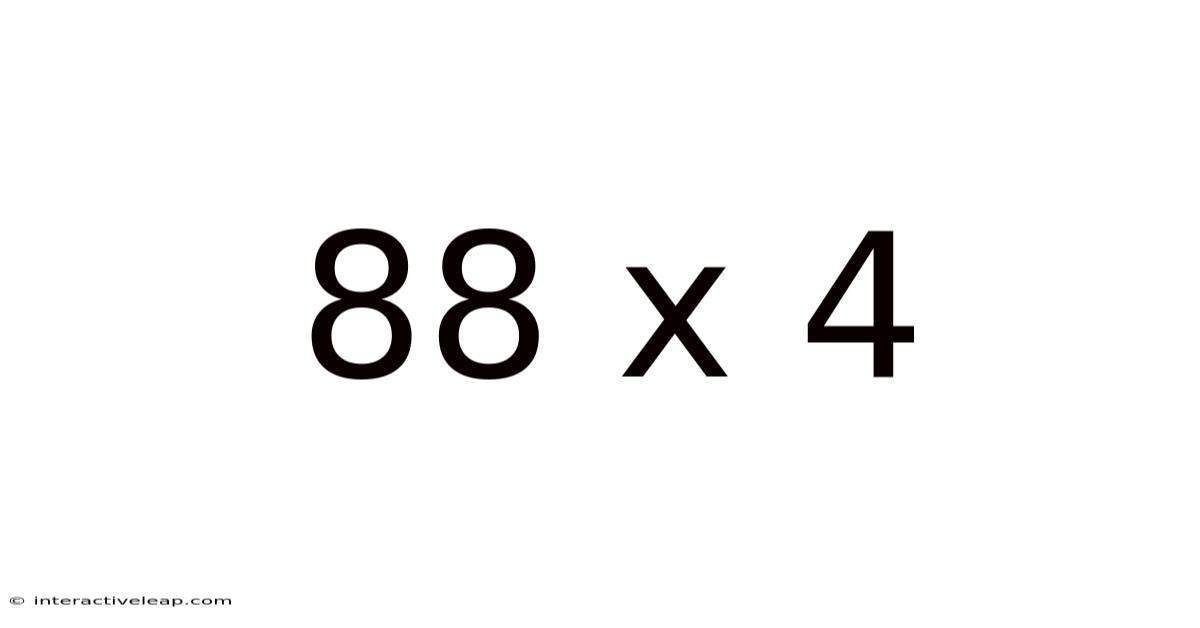
Table of Contents
Decoding 88 x 4: A Deep Dive into Multiplication and Beyond
This article explores the seemingly simple multiplication problem, 88 x 4, delving far beyond the immediate answer to uncover the underlying mathematical principles, explore various methods of solving it, and connect it to broader concepts in mathematics and beyond. Understanding this seemingly basic calculation offers a gateway to appreciating the elegance and power of mathematics. We'll examine different approaches, from basic multiplication to advanced techniques, making this exploration accessible to learners of all levels.
Introduction: More Than Just a Number
At first glance, 88 x 4 appears straightforward. A quick calculation reveals the answer: 352. However, this simple problem provides a fertile ground for exploring fundamental mathematical concepts and problem-solving strategies. This exploration will go beyond simply finding the solution; we will unpack the "why" behind the calculation, looking at its implications in various mathematical fields and even real-world applications. We’ll cover different methods of solving this problem, discuss the properties of numbers involved, and examine its relevance in more complex mathematical contexts.
Method 1: Standard Multiplication
The most common approach is standard long multiplication. This method involves breaking down the numbers and performing multiple smaller multiplications:
- Step 1: Multiply 88 by 4. Start with the ones column: 4 x 8 = 32. Write down the 2 and carry-over the 3.
- Step 2: Multiply 8 (in the tens column) by 4, and add the carried-over 3: (4 x 8) + 3 = 35. Write down 35.
- Step 3: The result is 352.
This method is foundational in arithmetic and is easily understood by most. Its simplicity makes it a cornerstone of early mathematical learning.
Method 2: Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this property to break down 88 x 4:
- Step 1: Rewrite 88 as 80 + 8.
- Step 2: Apply the distributive property: 4(80 + 8) = (4 x 80) + (4 x 8)
- Step 3: Calculate each part: (320) + (32) = 352
This method showcases a deeper understanding of mathematical properties and provides a more flexible approach to multiplication. It's particularly useful for larger numbers where mental calculation becomes more challenging.
Method 3: Doubling and Halving
This technique leverages the commutative property of multiplication (a x b = b x a). We can halve one number and double the other to simplify the calculation:
- Step 1: Halve 88: 88 / 2 = 44
- Step 2: Double 4: 4 x 2 = 8
- Step 3: Multiply the halved and doubled numbers: 44 x 8. This can be further simplified by doubling again: 22 x 16, then 11 x 32.
- Step 4: 11 x 32 = (10 x 32) + (1 x 32) = 320 + 32 = 352
While this method might seem more complex at first, it demonstrates the power of manipulating numbers to simplify calculations. This is particularly helpful with larger numbers or when dealing with mental mathematics.
Method 4: Using Arrays
Visual learners can benefit from representing multiplication using arrays. An array is a rectangular arrangement of objects where the number of rows and columns represent the factors being multiplied. For 88 x 4, we would have:
- 88 rows and 4 columns. While drawing this array might be impractical, we can visualize it. The total number of objects in the array represents the product.
This visual representation aids in understanding the concept of multiplication as repeated addition.
Understanding the Numbers: Factors and Multiples
The numbers involved, 88 and 4, have specific properties worth exploring.
- Factors: The factors of 88 are 1, 2, 4, 8, 11, 22, 44, and 88. The factors of 4 are 1, 2, and 4. Notice that 4 is a factor of 88, indicating that the multiplication will result in a whole number.
- Multiples: Multiples of 88 are numbers obtained by multiplying 88 by integers (e.g., 176, 264, 352...). 352 is a multiple of both 88 and 4.
- Prime Factorization: Breaking down numbers into their prime factors (numbers only divisible by 1 and themselves) provides deeper insights. The prime factorization of 88 is 2 x 2 x 2 x 11 (2³ x 11), and the prime factorization of 4 is 2 x 2 (2²). This shows the common factors between the two numbers.
Understanding the factor and multiple relationships provides a richer understanding of the numbers involved in the calculation.
Connecting to Broader Mathematical Concepts
The seemingly simple calculation 88 x 4 opens doors to more advanced mathematical concepts:
- Algebra: We can represent this calculation algebraically as x = 88 x 4. Solving for x gives us the answer. This simple equation introduces the fundamental concept of variables and equations.
- Geometry: The calculation can be visualized geometrically. Imagine a rectangle with sides measuring 88 units and 4 units. The area of this rectangle represents the product (352 square units). This connection bridges arithmetic with geometry.
- Number Theory: Exploring the properties of 88 and 4, such as their factors, multiples, and prime factorization, delves into the realm of number theory, a branch of mathematics focused on the properties of numbers.
- Real-world Applications: This calculation has practical applications in various fields. Imagine calculating the total cost of 88 items priced at $4 each, or the total distance covered in 4 hours at a speed of 88 miles per hour.
Frequently Asked Questions (FAQs)
-
Q: What is the quickest way to calculate 88 x 4?
- A: The quickest method often depends on individual preference and mathematical proficiency. Mental math using the distributive property (4 x (80 + 8)) or doubling and halving can be efficient.
-
Q: Why is it important to learn different methods of multiplication?
- A: Learning diverse methods enhances understanding, builds mathematical flexibility, and prepares individuals for more complex calculations. Different methods cater to different learning styles and problem-solving approaches.
-
Q: How can I improve my multiplication skills?
- A: Consistent practice, using various methods, working with different numbers, and understanding the underlying principles are crucial for enhancing multiplication skills.
Conclusion: The Power of Simple Calculations
The seemingly simple equation, 88 x 4, provides a gateway to exploring the vast world of mathematics. By investigating different solution methods, understanding the properties of numbers, and connecting the calculation to broader mathematical concepts, we unveil the richness and power embedded within even the most basic arithmetic. This exploration encourages a deeper appreciation for the elegance and practicality of mathematics, reminding us that even the simplest calculations hold significant depth and can illuminate fundamental mathematical principles. The journey from simply finding the answer (352) to understanding the "why" behind the calculation fosters critical thinking, problem-solving skills, and a stronger foundation for future mathematical learning. This deeper understanding moves beyond rote memorization, cultivating a genuine appreciation for the beauty and utility of mathematics in our daily lives.
Latest Posts
Latest Posts
-
3 4 Cos 13
Sep 13, 2025
-
30 Of 400
Sep 13, 2025
-
186cm In Ft
Sep 13, 2025
-
85g To Oz
Sep 13, 2025
-
34 X 12
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 88 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.