34 X 12
interactiveleap
Sep 13, 2025 · 5 min read
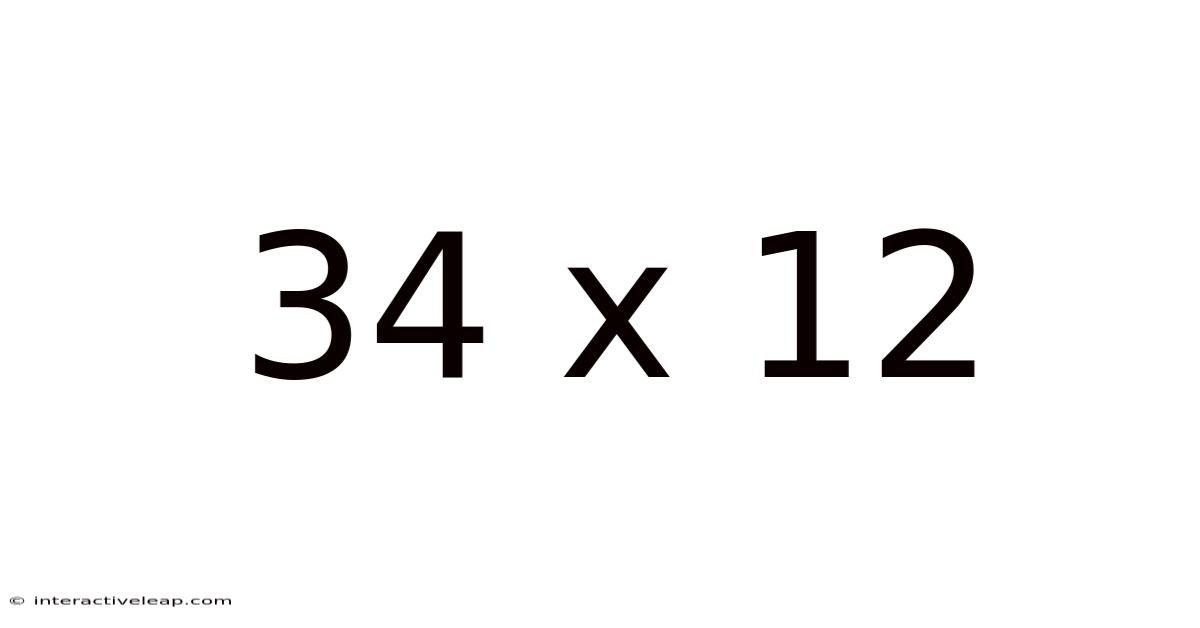
Table of Contents
Exploring the Multiplication Problem: 34 x 12 – A Deep Dive into Methods and Applications
This article delves into the seemingly simple multiplication problem, 34 x 12. While the answer might seem readily accessible with a calculator, exploring various methods of solving this problem reveals fundamental mathematical concepts and provides a foundation for understanding more complex calculations. We will explore different approaches, from basic multiplication to more advanced techniques, examining their practical applications and underlying principles. This in-depth analysis will be beneficial for students of all levels, reinforcing core mathematical skills and offering a deeper appreciation for the beauty and utility of numbers.
Introduction: The Power of Multiplication
Multiplication, at its core, represents repeated addition. The problem 34 x 12 means adding 34 twelve times, or adding 12 thirty-four times. While this approach is theoretically sound, it's not the most efficient method, especially for larger numbers. Therefore, understanding various multiplication techniques is crucial for efficiency and accuracy. This article will explore several methods to solve 34 x 12, highlighting their strengths and weaknesses.
Method 1: Standard Multiplication Algorithm
This is the most commonly taught method in schools. It involves breaking down the numbers into tens and units, performing multiplication for each place value, and then summing the results.
-
Step 1: Multiply 34 by the units digit of 12 (which is 2):
2 x 4 = 8 (units) 2 x 30 = 60 (tens)
-
Step 2: Multiply 34 by the tens digit of 12 (which is 1), remembering to add a zero as a placeholder in the units column:
10 x 4 = 40 (tens) 10 x 30 = 300 (hundreds)
-
Step 3: Add the results from Step 1 and Step 2:
68 (from Step 1)
- 340 (from Step 2)
408
Therefore, 34 x 12 = 408.
This method is systematic and easy to understand, forming the basis for multiplication of larger numbers. The understanding of place value is critical for successful application of this algorithm.
Method 2: Distributive Property
The distributive property of multiplication states that a(b + c) = ab + ac. We can use this property to simplify the calculation:
- Rewrite 12 as 10 + 2: 34 x (10 + 2)
- Apply the distributive property: (34 x 10) + (34 x 2)
- Calculate: 340 + 68 = 408
This method demonstrates a fundamental algebraic principle and provides an alternative approach to standard multiplication, highlighting the interconnectedness of arithmetic and algebra.
Method 3: Lattice Multiplication
Lattice multiplication, an ancient method, provides a visual approach to multiplication. It involves creating a grid, breaking down the numbers, and then performing simpler multiplications within the grid.
- Create a grid: A 2x2 grid is needed since both numbers have two digits.
- Fill the grid: Write the digits of 34 along the top and 12 along the right side.
- Multiply: Multiply each digit combination and write the result in the corresponding cell, splitting the tens and units digits diagonally.
- Sum the diagonals: Add the numbers along the diagonals, carrying over when necessary. The sum of the diagonals represents the final answer.
[Illustrative Diagram of Lattice Multiplication would go here. Due to the text-based nature of this response, I cannot create a visual diagram. However, a simple search for "lattice multiplication" will provide numerous visual examples.]
Lattice multiplication can be helpful for visualizing the process and is particularly useful for multiplying larger numbers.
Method 4: Mental Math Techniques
While not always as efficient for complex problems, understanding mental math techniques can improve speed and calculation ability. For 34 x 12, one approach is:
- Double and halve: Double 12 (to 24) and halve 34 (to 17). Now, multiply 17 x 24. This might still seem complex, but breaking it down further can simplify things.
- Breaking it down: 17 x 24 can be calculated as (17 x 20) + (17 x 4) = 340 + 68 = 408.
This method showcases flexibility in adapting to different approaches based on the specific numbers involved.
The Significance of Understanding Different Methods
Understanding multiple methods for solving 34 x 12 offers several advantages:
- Improved Number Sense: It enhances a deeper understanding of numerical relationships and operations.
- Problem-Solving Skills: It cultivates critical thinking and the ability to choose the most efficient method for a given problem.
- Foundation for Advanced Math: It builds a strong foundation for more complex mathematical concepts like algebra, calculus, and beyond. Understanding the distributive property, for example, is fundamental in algebra.
- Increased Confidence: Mastering different methods boosts confidence in tackling mathematical problems.
Applications of Multiplication: Beyond the Classroom
The seemingly simple problem of 34 x 12 has far-reaching applications in various real-world scenarios:
- Calculating Costs: Imagine buying 34 items that cost $12 each. The total cost is directly calculated using 34 x 12.
- Area Calculation: If you have a rectangular area measuring 34 units by 12 units, the total area is 34 x 12 square units.
- Data Analysis: Many data analysis tasks involve performing calculations similar to 34 x 12, whether it's determining totals, averages, or other statistical measures.
- Everyday Budgeting: Budgeting involves numerous multiplication calculations to track expenses, savings, and investment returns.
Frequently Asked Questions (FAQ)
-
Q: Is there only one correct way to solve 34 x 12?
- A: No, there are multiple correct methods, each with its own advantages and disadvantages. The best method depends on individual preference and the context of the problem.
-
Q: Why is it important to learn different multiplication methods?
- A: Learning multiple methods enhances understanding, improves problem-solving skills, and provides flexibility in approaching different problems.
-
Q: How can I improve my multiplication skills?
- A: Regular practice, utilizing different methods, and focusing on understanding the underlying principles are crucial for improvement.
-
Q: Are there online resources to help with multiplication practice?
- A: Yes, numerous online websites and educational apps offer interactive multiplication practice exercises.
Conclusion: Mastering Multiplication – A Journey of Understanding
The seemingly simple multiplication problem 34 x 12 serves as a gateway to a deeper understanding of fundamental mathematical concepts. By exploring various methods and appreciating their applications, we move beyond rote memorization to develop a robust mathematical foundation. The ability to approach this problem – and similar problems – using multiple techniques highlights not only computational skills but also critical thinking and problem-solving abilities. This versatility is invaluable, extending far beyond the classroom and into numerous aspects of daily life. Remember, the journey of mastering mathematics is a continuous process of exploration, understanding, and application. Embrace the different approaches, practice regularly, and enjoy the rewarding experience of unlocking the power of numbers.
Latest Posts
Latest Posts
-
139lbs In Kg
Sep 13, 2025
-
Nanogram To Gram
Sep 13, 2025
-
4 Of 500
Sep 13, 2025
-
Square Feet Sign
Sep 13, 2025
-
109kg To Pounds
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 34 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.