30/ Of 400
interactiveleap
Sep 13, 2025 · 5 min read
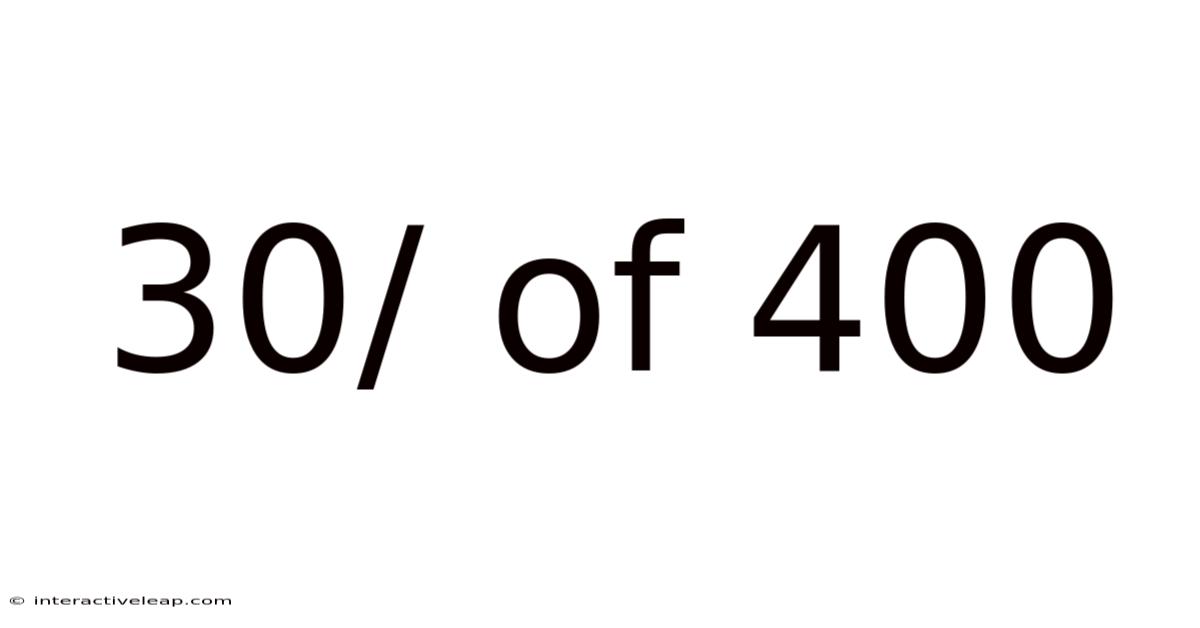
Table of Contents
Understanding 30/400: Fractions, Percentages, and Real-World Applications
What does 30/400 mean? This simple fraction might seem insignificant at first glance, but understanding how to interpret and manipulate it unlocks a world of practical applications in various fields, from basic arithmetic to advanced statistical analysis. This article will delve deep into the meaning of 30/400, exploring its representation as a fraction, decimal, and percentage, alongside numerous real-world examples to illustrate its relevance. We'll also cover simplifying fractions and address frequently asked questions to ensure a comprehensive understanding of this seemingly simple concept.
Breaking Down 30/400: The Basics
The fraction 30/400 represents 30 parts out of a total of 400 parts. This is a fundamental concept in understanding fractions. The number on top (30) is called the numerator, and the number on the bottom (400) is called the denominator. The denominator indicates the total number of equal parts, while the numerator indicates how many of those parts are being considered.
Simplifying the Fraction: Finding the Lowest Terms
Before delving into more complex representations, it's crucial to simplify the fraction 30/400. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 30 and 400 is 10.
Dividing both the numerator and denominator by 10, we get:
30 ÷ 10 = 3 400 ÷ 10 = 40
Therefore, the simplified fraction is 3/40. This simplified form is easier to work with and provides a clearer understanding of the proportion represented.
Converting to a Decimal: Understanding Proportions
To convert the fraction 3/40 to a decimal, we perform the division: 3 ÷ 40 = 0.075. This decimal representation (0.075) shows the proportional value of 30 out of 400 as a number between 0 and 1. This decimal form is particularly useful for calculations and comparisons in various applications, especially when dealing with percentages or data analysis.
Converting to a Percentage: Expressing Proportion as a Rate
Percentages provide a readily understandable way to express proportions. To convert the decimal 0.075 to a percentage, we multiply by 100:
0.075 x 100 = 7.5%
Therefore, 30/400 is equivalent to 7.5%. This means that 30 represents 7.5% of 400. This percentage representation is widely used in various contexts, such as expressing test scores, discounts, growth rates, and more.
Real-World Applications of 30/400 (or 3/40 or 7.5%)
The application of understanding 30/400 extends far beyond simple arithmetic. Here are some examples illustrating its practical use:
-
Test Scores: Imagine a test with 400 total points. A score of 30 points translates to a 7.5% score. This allows for easy comparison with other scores and provides a clear picture of performance.
-
Sales and Discounts: A store offering a 7.5% discount on an item priced at $400 would reduce the price by $30. Understanding this percentage is crucial for calculating the final price.
-
Surveys and Statistics: If 30 out of 400 respondents answered "yes" to a survey question, the 7.5% positive response rate provides valuable data for analysis and interpretation.
-
Financial Analysis: In finance, understanding proportions is critical for interpreting financial statements. For instance, if a company's debt is $30 million out of a total asset value of $400 million, the debt-to-asset ratio would be 7.5%, providing insights into the company’s financial health.
-
Project Management: In project management, tracking progress often involves assessing the completion of tasks. If 30 out of 400 tasks are completed, this represents 7.5% progress. This data informs further planning and resource allocation.
-
Manufacturing and Quality Control: In manufacturing, 30 defective units out of 400 produced would indicate a 7.5% defect rate. This information helps identify quality control issues and improve production processes.
Further Exploration: Working with Proportions
The concept of 30/400, simplified to 3/40 and represented as 7.5%, opens doors to solving various proportion problems. For example:
-
Finding a Part: If 7.5% of a quantity is 30, what is the total quantity? This is solved by setting up a proportion: 7.5/100 = 30/x. Solving for x (the total quantity) gives 400.
-
Finding a Percentage: What percentage is 15 out of 400? This can be calculated as (15/400) x 100 = 3.75%.
Frequently Asked Questions (FAQ)
Q: Can 30/400 be simplified further than 3/40?
A: No, 3/40 is the simplest form because 3 and 40 share no common factors other than 1.
Q: What if the numbers are larger, making simplification more challenging?
A: For larger numbers, find the prime factorization of both the numerator and denominator. Then, cancel out any common prime factors. This method ensures you arrive at the simplest form efficiently.
Q: Are there any online tools to simplify fractions?
A: Yes, numerous online calculators are available that can simplify fractions instantly. However, understanding the process manually is crucial for developing a strong foundational understanding of mathematics.
Q: What if I have a fraction where the numerator is larger than the denominator (an improper fraction)?
A: An improper fraction (e.g., 400/30) can be converted into a mixed number (e.g., 13 and 1/3) or a decimal (e.g., 13.333...). This often simplifies calculations and makes the value easier to interpret.
Q: How important is understanding fractions, decimals, and percentages in everyday life?
A: These concepts are fundamental to everyday life, from managing personal finances to understanding statistical data and making informed decisions in various aspects of life.
Conclusion: Mastering the Fundamentals
Understanding the meaning and applications of 30/400, whether expressed as a fraction, decimal, or percentage, demonstrates the power of fundamental mathematical concepts. The ability to simplify fractions, convert between different representations, and apply these concepts to real-world scenarios is a valuable skill that extends far beyond the classroom. By mastering these fundamental principles, you equip yourself with tools for effective problem-solving and enhanced comprehension of numerical data in diverse fields. The seemingly simple fraction 30/400 serves as a gateway to understanding more complex mathematical ideas and their relevance to our daily lives.
Latest Posts
Latest Posts
-
121mm In Inches
Sep 13, 2025
-
1600m In Miles
Sep 13, 2025
-
Mali Vrs Ghana
Sep 13, 2025
-
139lbs In Kg
Sep 13, 2025
-
Nanogram To Gram
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 30/ Of 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.