85 Of 500
interactiveleap
Sep 25, 2025 · 5 min read
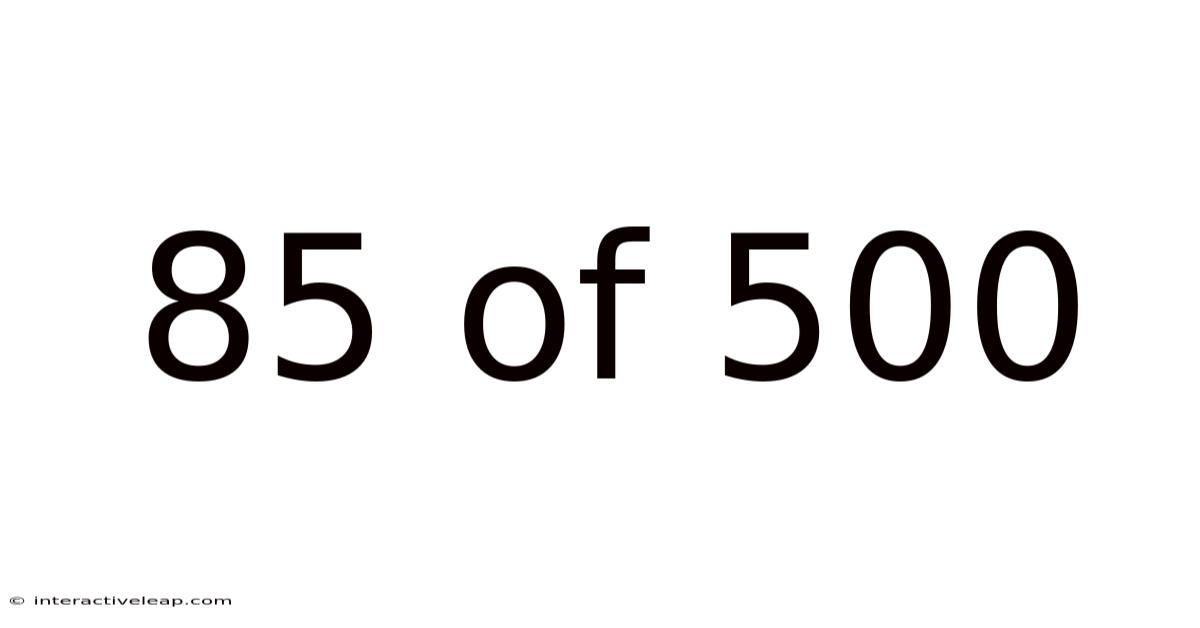
Table of Contents
Decoding 85 out of 500: Understanding Percentages, Proportions, and Applications
Understanding fractions, percentages, and proportions is fundamental to many areas of life, from calculating your grades to understanding financial reports. This article delves deep into the meaning of "85 out of 500," explaining how to calculate the percentage, its practical applications, and answering frequently asked questions. We'll explore the broader mathematical concepts involved, ensuring you gain a comprehensive understanding beyond just a simple numerical answer.
Introduction: What Does 85 out of 500 Mean?
The phrase "85 out of 500" represents a fraction or a ratio. It signifies that 85 items or units are selected or achieved from a total of 500 possible items or units. This type of representation is common in many contexts, including academic scores, survey results, manufacturing quality control, and various statistical analyses. Understanding how to express this ratio as a percentage and interpret its meaning is crucial for making informed decisions and comprehending data. This article will guide you through the process, providing clear explanations and real-world examples.
1. Calculating the Percentage:
The most common way to represent "85 out of 500" is as a percentage. A percentage expresses a fraction as a portion of 100. To calculate the percentage, follow these steps:
-
Step 1: Formulate the Fraction: Express "85 out of 500" as a fraction: 85/500.
-
Step 2: Convert to Decimal: Divide the numerator (85) by the denominator (500): 85 ÷ 500 = 0.17
-
Step 3: Convert Decimal to Percentage: Multiply the decimal by 100 and add the percentage symbol (%): 0.17 x 100 = 17%
Therefore, 85 out of 500 is equal to 17%.
2. Understanding Proportions and Ratios:
The concept of "85 out of 500" is inherently linked to proportions and ratios. A ratio compares two quantities, while a proportion states that two ratios are equal.
-
Ratio: The ratio of successful attempts to total attempts is 85:500 (or simplified to 17:100). This shows the relative size of the two quantities.
-
Proportion: We can use this ratio to solve problems involving proportions. For example, if there were 1000 attempts, we can set up a proportion to find the expected number of successful attempts:
85/500 = x/1000
Solving for x (cross-multiplying): 500x = 85000
x = 170
This means we would expect 170 successful attempts out of 1000, maintaining the same proportion.
3. Practical Applications:
The concept of "85 out of 500" has diverse practical applications across many fields:
-
Academic Performance: If 85 out of 500 students passed an exam, the pass rate is 17%. This allows educators to assess the effectiveness of teaching methods and identify areas needing improvement.
-
Quality Control: In a manufacturing setting, if 85 out of 500 products are defective, the defect rate is 17%. This information is crucial for identifying production bottlenecks and improving product quality.
-
Market Research: If 85 out of 500 respondents in a survey prefer a particular product, the preference rate is 17%. This data can guide marketing strategies and product development.
-
Statistical Analysis: In statistical analysis, this data point can be used in various calculations, like calculating confidence intervals or performing hypothesis tests. This helps draw conclusions about larger populations based on sample data.
-
Finance: In financial analysis, this ratio could represent the percentage of successful investments or the percentage of loans repaid. This information is crucial for evaluating investment strategies and credit risk.
-
Health and Medicine: In clinical trials or epidemiological studies, this could represent the success rate of a treatment or the prevalence of a disease within a specific population. This information is crucial for informing healthcare decisions and improving public health.
4. Advanced Concepts and Further Exploration:
Understanding "85 out of 500" opens doors to more complex mathematical and statistical concepts:
-
Standard Deviation and Normal Distribution: If we know the standard deviation of the data set (the 500 attempts), we can determine how unusual a score of 85 is. This involves exploring concepts like the normal distribution and z-scores.
-
Confidence Intervals: Using statistical methods, we can calculate a confidence interval around the 17% success rate. This gives a range within which the true population percentage is likely to fall.
-
Hypothesis Testing: We can use this data to test hypotheses about the underlying population. For instance, we might test the hypothesis that the true success rate is different from 20%.
-
Regression Analysis: If we have other relevant variables (e.g., study time for academic performance, manufacturing process variables for quality control), we could use regression analysis to model the relationship between these variables and the outcome (85 out of 500).
5. Frequently Asked Questions (FAQs):
-
Q: How do I express 85 out of 500 as a decimal?
- A: Divide 85 by 500: 85/500 = 0.17
-
Q: Can I simplify the fraction 85/500?
- A: Yes, both the numerator and denominator are divisible by 5. Simplifying gives you 17/100, which is equivalent to 17%.
-
Q: What if I have a different number of successful attempts and total attempts?
- A: The same principles apply. Simply replace 85 and 500 with your specific numbers and follow the steps to calculate the percentage.
-
Q: Why is understanding percentages important?
- A: Percentages allow us to easily compare proportions, make informed decisions based on data, and communicate information effectively across various fields.
-
Q: How can I improve my understanding of proportions and ratios?
- A: Practice solving various problems involving proportions and ratios. Work through examples from textbooks or online resources.
6. Conclusion: Beyond the Numbers
Understanding the meaning and implications of "85 out of 500" goes beyond simply calculating a percentage. It involves grasping the underlying principles of fractions, ratios, proportions, and their diverse applications across numerous fields. By mastering these concepts, you gain valuable tools for interpreting data, solving problems, and making informed decisions in various aspects of your life, from academics and professional endeavors to personal finance and everyday situations. The ability to interpret and analyze such data empowers you to understand trends, make predictions, and contribute meaningfully to any context you encounter. Remember that the number itself (17% in this case) is just the starting point for deeper analysis and understanding. The context in which this data is presented dictates the meaningful interpretations that can be drawn from it. Always consider the context and what the number truly represents.
Latest Posts
Latest Posts
-
20 Of 390
Sep 25, 2025
-
135kg In Lbs
Sep 25, 2025
-
Juice Wrld Artwork
Sep 25, 2025
-
0 09 To Percentage
Sep 25, 2025
-
Ocean Parkway Brooklyn
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 85 Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.