0.09 To Percentage
interactiveleap
Sep 25, 2025 · 5 min read
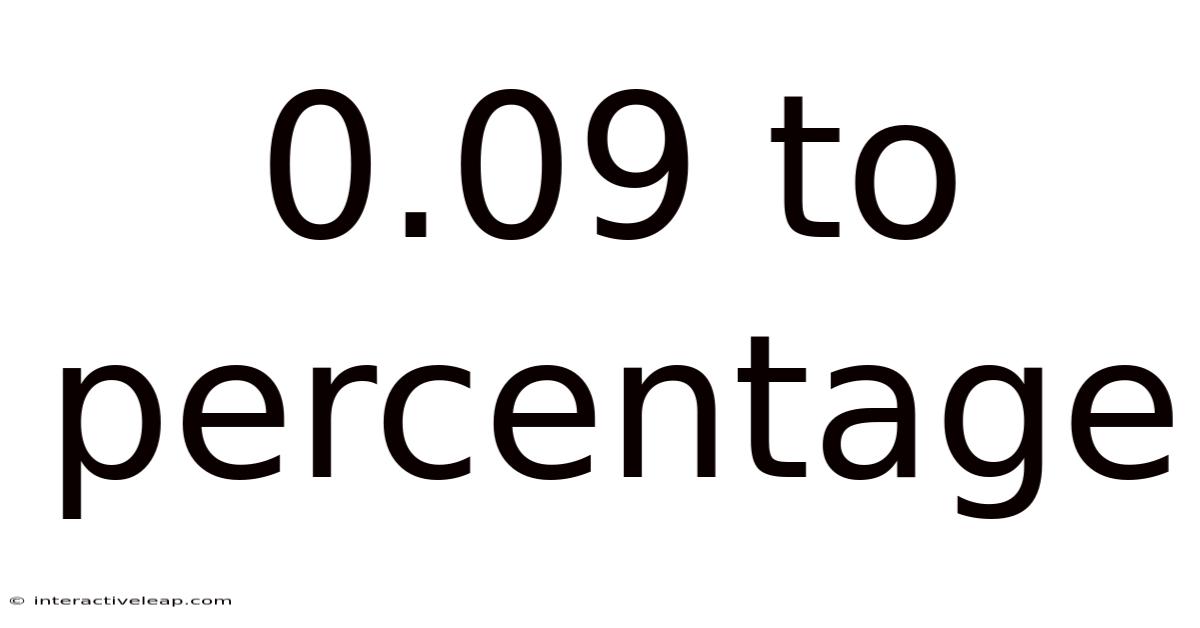
Table of Contents
From 0.09 to Percentage: A Comprehensive Guide
Converting decimals to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday calculations. This comprehensive guide will walk you through the process of converting the decimal 0.09 to a percentage, explaining the underlying principles and providing practical examples to solidify your understanding. We'll also delve into the broader context of decimal-to-percentage conversions, equipping you with the knowledge to tackle similar problems with confidence. Understanding this seemingly simple conversion is crucial for anyone seeking to improve their numerical literacy and problem-solving abilities.
Understanding Decimals and Percentages
Before we dive into the conversion, let's refresh our understanding of decimals and percentages. A decimal is a way of representing a number that is not a whole number. It uses a decimal point to separate the whole number part from the fractional part. For example, 0.09 represents nine hundredths.
A percentage, denoted by the symbol %, represents a fraction of 100. It indicates how many parts of a whole there are if the whole is divided into 100 equal parts. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Converting 0.09 to a Percentage
The conversion from a decimal to a percentage involves a simple multiplication. To convert a decimal to a percentage, you multiply the decimal by 100 and then add the percentage symbol (%).
Here's how to convert 0.09 to a percentage:
- Multiply by 100: 0.09 x 100 = 9
- Add the percentage symbol: 9%
Therefore, 0.09 is equal to 9%.
The Underlying Mathematical Principle
The reason we multiply by 100 is rooted in the definition of percentage. A percentage is essentially a fraction with a denominator of 100. When we have a decimal like 0.09, it can be expressed as a fraction: 9/100. To express this fraction as a percentage, we simply state the numerator (9) and add the percentage symbol, resulting in 9%. Multiplying by 100 is a shortcut that achieves the same result. It essentially scales the decimal up to represent it as parts per hundred.
Practical Applications and Examples
The conversion of decimals to percentages is ubiquitous in various real-world scenarios. Let's explore a few examples:
-
Finance: Interest rates are often expressed as percentages. If a bank offers an annual interest rate of 0.09, it's equivalent to a 9% interest rate. Understanding this conversion allows you to compare different financial offers effectively.
-
Statistics: Data representation frequently involves percentages. If a survey shows that 0.09 of respondents prefer a particular product, this translates to 9% preference. This percentage provides a clear and concise way to understand the data.
-
Discounts: Sales often advertise discounts as percentages. A 0.09 discount on an item is equivalent to a 9% discount. This allows consumers to quickly calculate the price reduction.
-
Test Scores: If you scored 0.09 on a test (assuming a maximum score of 1), your score is equivalent to 9%.
-
Probability: In probability calculations, 0.09 represents a probability of 9%. This means that there's a 9% chance of a specific event occurring.
Working with Larger and Smaller Decimals
The process remains the same for decimals larger or smaller than 0.09. Let's consider a few more examples:
- Converting 0.5 to a percentage: 0.5 x 100 = 50%.
- Converting 1.25 to a percentage: 1.25 x 100 = 125%. Note that percentages can be greater than 100%.
- Converting 0.005 to a percentage: 0.005 x 100 = 0.5%.
- Converting 2.7 to a percentage: 2.7 x 100 = 270%
Converting Percentages to Decimals (Reverse Operation)
The reverse operation, converting a percentage to a decimal, is equally important. To convert a percentage to a decimal, you divide the percentage by 100 and remove the percentage symbol.
For example, to convert 9% to a decimal:
- Divide by 100: 9 / 100 = 0.09
This confirms our earlier conversion.
Dealing with Percentages Greater than 100%
As mentioned earlier, percentages can be greater than 100%. This simply indicates that the value is more than the whole. For example, if a quantity increases by 120%, it means it has increased to 220% of its original value (100% + 120% = 220%). The corresponding decimal would be 2.2 (220/100 = 2.2).
Frequently Asked Questions (FAQ)
Q1: Why do we use percentages?
A1: Percentages provide a standardized way to represent proportions and fractions. They make it easier to compare different quantities and understand relative changes or proportions. They are universally understood and simplify the communication of numerical data.
Q2: What if I have a decimal with more than two places after the decimal point?
A2: The process remains the same. Simply multiply the decimal by 100 and add the percentage symbol. For example, 0.095 x 100 = 9.5%, and 0.1234 x 100 = 12.34%.
Q3: Can I use a calculator to perform this conversion?
A3: Absolutely! Most calculators have a percentage function that simplifies this conversion. Simply enter the decimal, press the multiplication key, enter 100, and press the equals key. The result will be the percentage equivalent.
Q4: What are some common mistakes to avoid when converting decimals to percentages?
A4: The most common mistake is forgetting to multiply by 100. Another mistake is misplacing the decimal point when performing the multiplication. Always double-check your calculations to ensure accuracy.
Conclusion
Converting decimals to percentages, such as transforming 0.09 to 9%, is a fundamental mathematical skill with practical applications across diverse fields. Understanding the underlying principles, along with practice, will empower you to confidently perform these conversions and interpret numerical data effectively. Remember the simple steps: multiply the decimal by 100 and add the percentage symbol. This seemingly small skill significantly enhances your numerical literacy and problem-solving capabilities in everyday life and professional contexts. The ability to seamlessly translate between decimals and percentages is a cornerstone of numerical fluency, crucial for navigating a data-rich world.
Latest Posts
Latest Posts
-
85 25 Off
Sep 25, 2025
-
Adjectives For Sand
Sep 25, 2025
-
15 Off 48
Sep 25, 2025
-
10 Of 950
Sep 25, 2025
-
84 7kg To Lbs
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 0.09 To Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.