20 Of 390
interactiveleap
Sep 25, 2025 · 5 min read
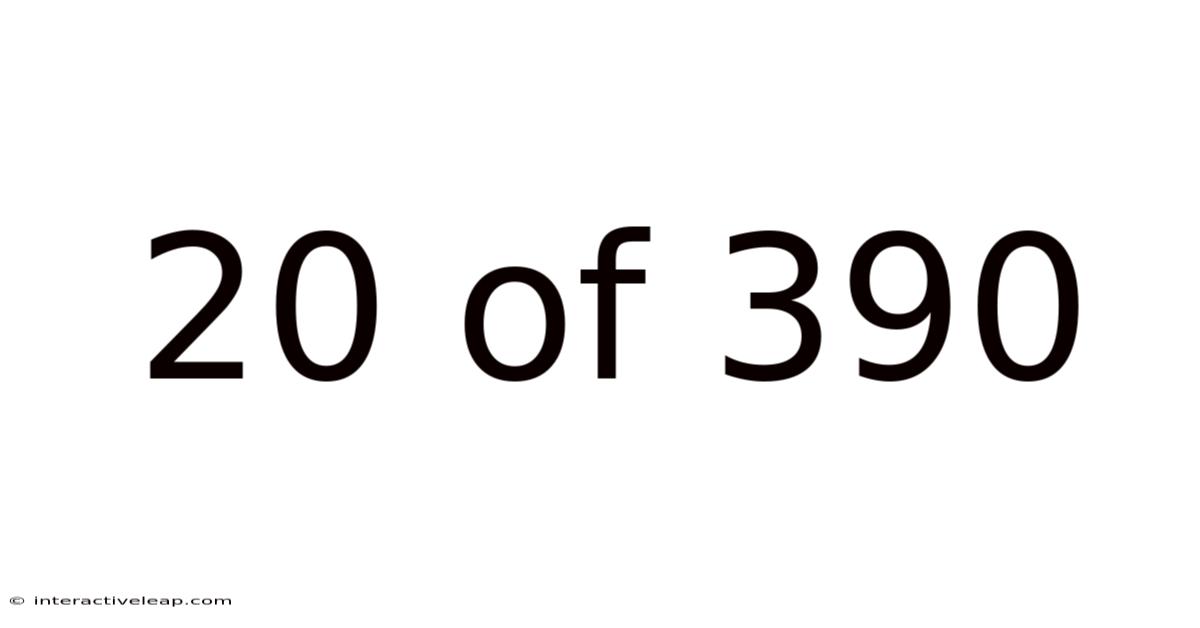
Table of Contents
Decoding 20 of 390: Understanding Fractions, Ratios, and Proportions
The seemingly simple phrase "20 of 390" hides a wealth of mathematical concepts. At first glance, it might seem like just a simple statement of quantity. However, understanding its deeper meaning unlocks the world of fractions, ratios, and proportions – fundamental concepts crucial in various fields, from everyday life to advanced scientific calculations. This article will delve deep into what "20 of 390" represents, exploring its implications and practical applications. We'll uncover how to simplify this expression, analyze its proportional relationships, and understand its significance in different contexts.
Introduction: Understanding the Fundamentals
"20 of 390" describes a part-to-whole relationship. It tells us that there are 20 items out of a total of 390 items. This instantly translates into a fraction, a mathematical representation of a part of a whole. In this case, the fraction is 20/390. Understanding fractions is the cornerstone of comprehending ratios and proportions.
A fraction consists of two parts: the numerator (the top number, representing the part) and the denominator (the bottom number, representing the whole). In our example, 20 is the numerator, and 390 is the denominator.
A ratio compares two quantities. While a fraction represents a part of a whole, a ratio can compare any two numbers, not necessarily a part to a whole. "20 of 390" can also be expressed as a ratio of 20:390 (20 to 390). This ratio indicates the relative size of 20 compared to 390.
A proportion is a statement of equality between two ratios. For example, if we had another ratio, say 2:39, we could determine if it's proportional to 20:390 by checking if the ratios are equivalent. This involves cross-multiplication and checking if the products are equal.
Simplifying the Fraction: Finding the Simplest Form
The fraction 20/390 is not in its simplest form. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 20 and 390 is 10.
Dividing both the numerator and the denominator by 10, we get:
20 ÷ 10 = 2 390 ÷ 10 = 39
Therefore, the simplest form of the fraction 20/390 is 2/39. This simplified fraction retains the same proportional relationship as the original fraction but is easier to work with and understand. This simplification process is crucial for various mathematical calculations and simplifies the interpretation of the data.
Calculating the Percentage: Expressing the Part as a Percentage of the Whole
Converting the fraction to a percentage provides another way to represent the part-to-whole relationship. To convert a fraction to a percentage, we multiply the fraction by 100%.
(2/39) * 100% ≈ 5.13%
This means that 20 out of 390 represents approximately 5.13% of the total. Expressing the data as a percentage is useful for comparison and understanding the relative magnitude of the part compared to the whole. Percentages are widely used in various fields, including finance, statistics, and everyday life.
Real-World Applications: Examples of 20 of 390 in Different Contexts
The interpretation and application of "20 of 390" heavily depend on the context. Here are a few examples:
-
Inventory Management: Imagine a warehouse with 390 items. If 20 of them are damaged, the fraction 2/39 represents the proportion of damaged goods. This information is vital for inventory control and loss assessment.
-
Survey Results: In a survey of 390 people, if 20 responded positively to a particular question, the fraction 2/39 represents the proportion of positive responses. This is crucial for analyzing survey results and drawing meaningful conclusions.
-
Statistical Analysis: In a sample of 390 observations, if 20 exhibit a particular characteristic, the fraction 2/39 represents the sample proportion. This forms the basis for statistical inferences about the larger population.
-
Quality Control: In a batch of 390 manufactured parts, if 20 are defective, the fraction 2/39 represents the defect rate. This information is vital for quality control and process improvement.
-
Probability: If you randomly select one item from a set of 390 items, where 20 have a specific attribute, the probability of selecting an item with that attribute is 2/39.
Understanding Proportions: Scaling Up and Down
Proportions are fundamental in scaling up or down quantities. If we know that 20 out of 390 items have a certain characteristic, we can use proportions to determine how many items would have that characteristic in a larger or smaller set.
For instance, if we had 780 items (double the original amount), we could set up a proportion:
20/390 = x/780
Solving for x (using cross-multiplication):
390x = 20 * 780 x = (20 * 780) / 390 x = 40
This shows that in a set of 780 items, we would expect 40 items to have the same characteristic, maintaining the same proportion.
Further Exploration: Advanced Applications
The concept extends beyond simple calculations. Advanced applications include:
-
Financial Modeling: Calculating interest rates, returns on investment, and risk assessments often involve proportional reasoning.
-
Engineering and Physics: Scaling designs, calculating forces, and analyzing mechanical systems rely heavily on proportions.
-
Computer Science: Algorithm design and data structures often utilize proportional relationships for efficiency and optimization.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between a fraction and a ratio?
- A: While both compare quantities, a fraction always represents a part of a whole, while a ratio can compare any two quantities.
-
Q: How do I convert a fraction to a decimal?
- A: Divide the numerator by the denominator. For 2/39, this is approximately 0.0513.
-
Q: What is the significance of simplifying a fraction?
- A: Simplifying makes the fraction easier to understand, compare, and use in calculations.
-
Q: How can I use proportions to solve real-world problems?
- A: Set up an equation with two equivalent ratios, and solve for the unknown variable using cross-multiplication.
Conclusion: The Importance of Understanding Proportional Relationships
"20 of 390" is more than just a statement of quantity; it's a gateway to understanding fundamental mathematical concepts. Mastering fractions, ratios, and proportions is crucial for success in various fields. By understanding the relationships between these concepts and their practical applications, we can analyze data, solve problems, and make informed decisions in countless situations. The ability to simplify fractions, convert them to percentages, and understand proportional relationships is a valuable skill applicable throughout life, from everyday tasks to complex scientific endeavors. The seemingly simple phrase holds the key to a deeper understanding of the world around us, highlighting the power of mathematics in everyday life.
Latest Posts
Latest Posts
-
85 25 Off
Sep 25, 2025
-
Adjectives For Sand
Sep 25, 2025
-
15 Off 48
Sep 25, 2025
-
10 Of 950
Sep 25, 2025
-
84 7kg To Lbs
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 20 Of 390 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.