72 X 3
interactiveleap
Sep 21, 2025 · 5 min read
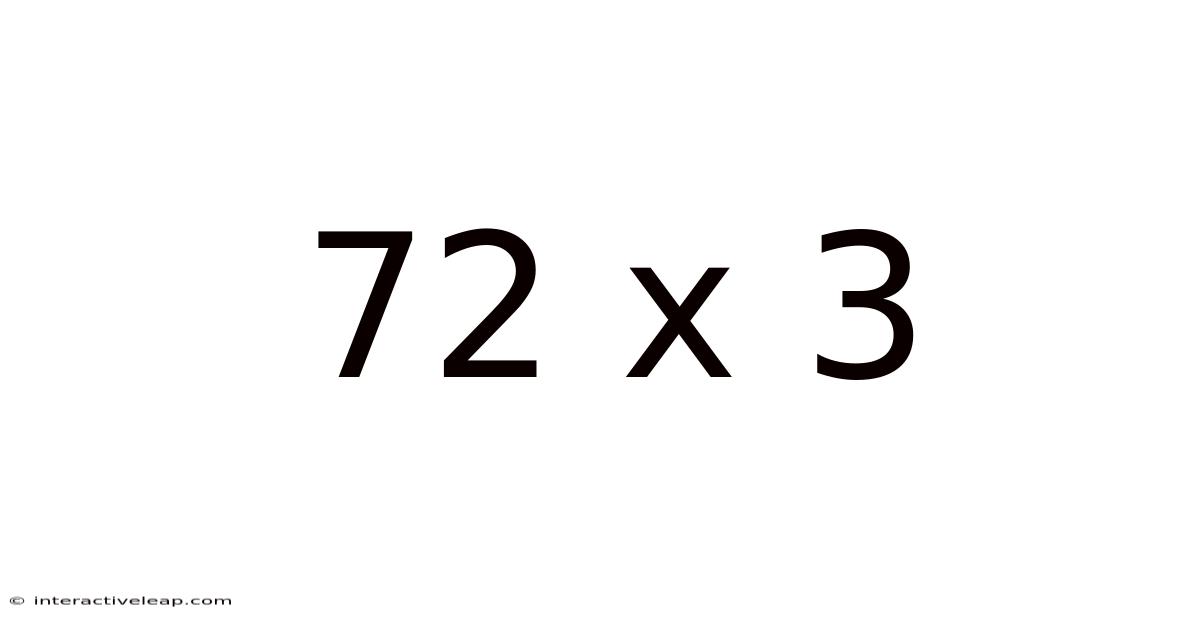
Table of Contents
Unpacking 72 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 72 x 3, far beyond the immediate answer. We'll delve into the fundamental concepts of multiplication, explore different methods for solving this problem, uncover its practical applications in various fields, and even touch upon the fascinating history of multiplication itself. This comprehensive guide is designed for learners of all levels, from elementary school students grasping the basics to adults seeking a deeper understanding of mathematical principles.
Understanding Multiplication: The Building Blocks
Multiplication is a fundamental arithmetic operation representing repeated addition. When we say 72 x 3, we're essentially saying "add 72 to itself three times." This seemingly simple concept forms the basis of countless mathematical operations and real-world applications. Understanding this core principle is crucial before we delve into the various methods of solving 72 x 3.
- Repeated Addition: 72 + 72 + 72 = 216
- Arrays: Imagine a rectangular array with 72 rows and 3 columns. The total number of items in the array represents 72 x 3. Visualizing this can be helpful, particularly for beginners.
- Scaling: Multiplication can be viewed as scaling. If you have 72 apples, and you triple that amount, you'll have 72 x 3 = 216 apples. This scaling concept is frequently used in various real-world scenarios.
Methods for Solving 72 x 3
Several methods can efficiently solve 72 x 3. Let's examine some common approaches:
1. Standard Multiplication Algorithm
This is the most common method taught in schools. It involves multiplying each digit of 72 by 3, starting with the ones place and carrying over any tens to the next place value:
72
x 3
------
216
- Ones place: 3 x 2 = 6
- Tens place: 3 x 7 = 21. The 21 is placed as 2 tens and 1 one, resulting in 216.
2. Distributive Property
The distributive property states that a(b + c) = ab + ac. We can apply this to break down 72 into smaller, easier-to-handle numbers:
72 x 3 = (70 + 2) x 3 = (70 x 3) + (2 x 3) = 210 + 6 = 216
This method is particularly useful for mental calculations and demonstrates a deeper understanding of mathematical principles.
3. Lattice Multiplication
Lattice multiplication is a visual method that can be helpful for larger numbers and for understanding the place value system. It involves creating a grid and performing individual multiplications within each cell:
[Imagine a 2x2 grid here. The top would have 7 and 2. The side would have 3. The inner squares would show 21 (7x3) and 6 (2x3). The diagonals would be added to get 216.]
While this method might seem more complex at first, it can improve understanding of the underlying principles of multiplication.
4. Using a Calculator
For quick calculations, a calculator provides a convenient and accurate solution. However, it's essential to understand the underlying mathematical concepts even when using a calculator.
Real-World Applications of 72 x 3 (and Multiplication in General)
The seemingly simple problem 72 x 3 has countless practical applications. Understanding multiplication is crucial in various fields:
- Everyday Finances: Calculating the total cost of three items priced at $72 each.
- Construction and Engineering: Determining the amount of material needed for a project (e.g., three sections of a 72-meter fence).
- Cooking and Baking: Scaling recipes – tripling a recipe that calls for 72 grams of flour.
- Science: Calculating quantities in experiments and analyzing data (e.g., three sets of 72 data points).
- Business: Calculating revenue, profit, and other financial aspects.
Exploring the History of Multiplication
Multiplication has a rich history, evolving over centuries alongside the development of mathematics. Early civilizations used various methods for multiplication, including:
- Egyptian Multiplication: A method relying on doubling and adding.
- Babylonian Multiplication: Used a sexagesimal system (base-60).
- Greek Multiplication: Employed geometric methods.
- Roman Multiplication: Based on Roman numerals and involved complex procedures.
The development of modern multiplication algorithms, including the standard algorithm, contributed significantly to simplifying calculations and advancing mathematical understanding.
Beyond 72 x 3: Expanding Mathematical Understanding
The problem 72 x 3 provides a springboard for exploring broader mathematical concepts:
- Factors and Multiples: Understanding the factors of 72 and the multiples of 3 helps to grasp the relationships between numbers.
- Prime Factorization: Breaking down 72 into its prime factors (2³ x 3²) provides insight into its structure.
- Algebra: Generalizing the concept to expressions like axb, where 'a' and 'b' represent variables, introduces the fundamental principles of algebra.
Frequently Asked Questions (FAQ)
- What is the answer to 72 x 3? The answer is 216.
- What are some alternative ways to calculate 72 x 3? We explored several methods including the standard algorithm, distributive property, lattice multiplication, and using a calculator.
- Why is learning multiplication important? Multiplication is a fundamental operation used in numerous aspects of life, from everyday calculations to complex scientific and engineering tasks.
- How can I improve my multiplication skills? Practice is key! Regular practice, using various methods and working through different problem types, will significantly improve your multiplication skills.
Conclusion: Mastering Multiplication and its Applications
The seemingly straightforward problem, 72 x 3, unveils a world of mathematical concepts and real-world applications. By exploring different methods of calculation, understanding the history of multiplication, and grasping the broader mathematical principles it embodies, we gain a deeper appreciation for this fundamental arithmetic operation. The ability to perform multiplication efficiently and accurately is a valuable skill applicable across diverse fields and essential for navigating the complexities of the modern world. This journey beyond the simple calculation of 72 x 3 reveals the power and beauty of mathematics, encouraging continued exploration and discovery in the fascinating world of numbers.
Latest Posts
Latest Posts
-
Wallaby Way Sydney
Sep 21, 2025
-
40 Of 175
Sep 21, 2025
-
Amp To Mamp
Sep 21, 2025
-
1 79 In Feet
Sep 21, 2025
-
Four Vowel Words
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 72 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.