40 Of 175
interactiveleap
Sep 21, 2025 · 6 min read
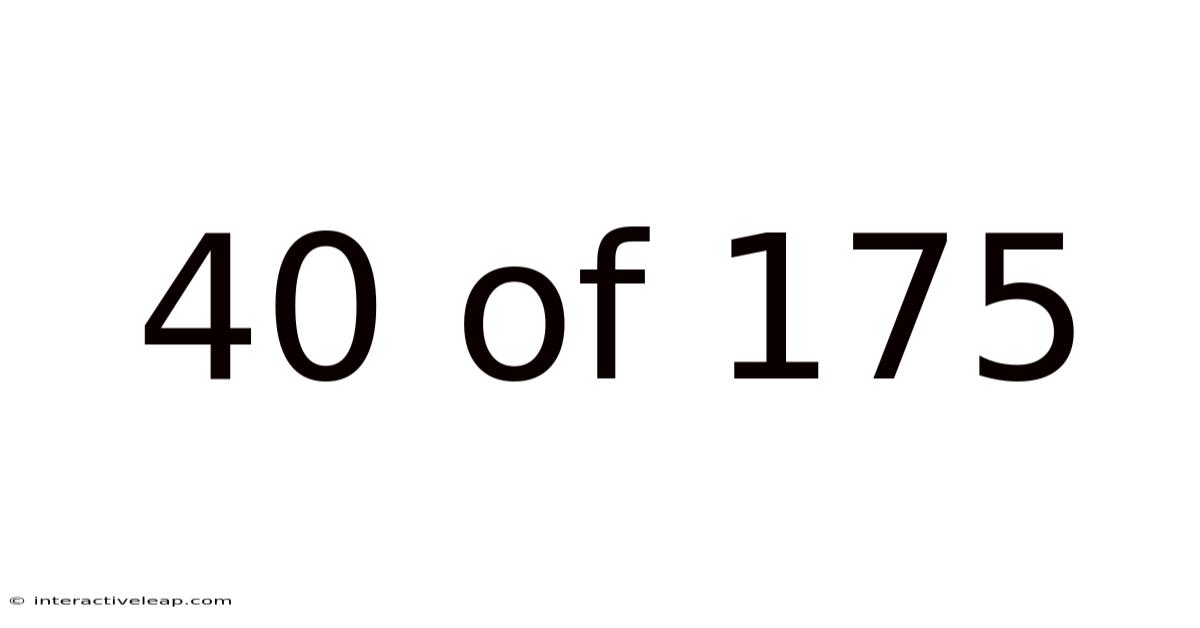
Table of Contents
Decoding 40 of 175: Understanding Fractions and Their Applications
The seemingly simple fraction "40 of 175" presents a common mathematical challenge, especially for those who struggle with understanding fractions and percentages. This article delves deep into the meaning of this fraction, exploring various methods for solving it, explaining its underlying mathematical principles, and highlighting its practical applications in everyday life. We'll uncover how to simplify, calculate, and interpret this fraction, empowering you with a stronger grasp of fundamental mathematical concepts. By the end, you'll be able to confidently tackle similar fractional problems and appreciate their relevance beyond the classroom.
Understanding the Fundamentals: What Does "40 of 175" Mean?
The expression "40 of 175" represents a part-to-whole relationship. It signifies 40 out of a total of 175 units. Think of it like having 175 apples, and selecting 40 of them. This fractional representation can be written as 40/175, indicating 40 is the numerator (the part) and 175 is the denominator (the whole). Understanding this basic representation is crucial for all subsequent calculations and interpretations.
Method 1: Simplifying the Fraction
Before performing any complex calculations, simplifying the fraction is often the most efficient first step. This involves finding the greatest common divisor (GCD) of both the numerator (40) and the denominator (175). The GCD is the largest number that divides both numbers without leaving a remainder.
To find the GCD of 40 and 175, we can use the Euclidean algorithm or prime factorization. Let's use prime factorization:
- Prime factorization of 40: 2 x 2 x 2 x 5 = 2³ x 5
- Prime factorization of 175: 5 x 5 x 7 = 5² x 7
The common factor between 40 and 175 is 5. Dividing both the numerator and the denominator by 5 gives us:
40/5 = 8 175/5 = 35
Therefore, the simplified fraction is 8/35. This simplified form is easier to work with in subsequent calculations and provides a clearer representation of the proportion.
Method 2: Converting to a Percentage
Converting a fraction to a percentage provides a readily understandable representation of the proportion. To convert 40/175 (or its simplified form 8/35) to a percentage, we perform the following steps:
- Divide the numerator by the denominator: 40 ÷ 175 ≈ 0.2286
- Multiply the result by 100: 0.2286 x 100 ≈ 22.86%
Therefore, 40 out of 175 represents approximately 22.86%. This percentage clearly indicates that 40 represents roughly a quarter of 175.
Method 3: Converting to a Decimal
Converting the fraction to a decimal provides another way to visualize the proportion. This is simply done by dividing the numerator by the denominator:
40 ÷ 175 ≈ 0.2286
Thus, 40 of 175 is approximately 0.2286 as a decimal. This decimal representation is useful for comparison with other decimals or in calculations involving decimals.
Real-World Applications of Fractions: Beyond the Textbook
Fractions are not just abstract mathematical concepts; they are fundamental tools used across numerous real-world scenarios. Understanding "40 of 175" and similar fractions translates into practical skills applicable in:
-
Business and Finance: Calculating profit margins, market share, and financial ratios often involve fractional calculations. For instance, if a company sold 40 units out of a total of 175 produced, understanding this fraction helps determine the sales performance.
-
Data Analysis and Statistics: Representing proportions and percentages within larger datasets frequently uses fractions. For example, if a survey of 175 people showed 40 preferred a specific product, this fractional representation is crucial in data interpretation and decision-making.
-
Science and Engineering: Fractions are vital in many scientific measurements and calculations, including calculating concentrations, ratios, and proportions in various experiments and engineering designs. In chemistry, for instance, accurately measuring and mixing reagents often requires precise fractional calculations.
-
Cooking and Baking: Following recipes often involves working with fractions. Understanding the relationship between ingredients and adjusting recipes based on the number of servings requires a firm grasp of fractional calculations.
-
Everyday Life: From sharing items equally among friends to determining discounts and sales, fractions permeate our daily routines. The ability to quickly calculate and understand fractions significantly improves problem-solving skills in many everyday contexts.
Exploring Further: Understanding Ratios and Proportions
The concept of "40 of 175" is closely linked to ratios and proportions. A ratio expresses the quantitative relationship between two or more amounts. In this case, the ratio is 40:175, indicating the proportion between the part (40) and the whole (175). Proportions are statements of equality between two ratios, allowing us to solve for unknown quantities in similar situations.
For example, we could set up a proportion to solve for an unknown quantity:
If 40 out of 175 items are defective, how many defective items would we expect in a batch of 525 items?
We can set up the proportion:
40/175 = x/525
Solving for x gives us:
x = (40 x 525) / 175 = 120
Therefore, we would expect 120 defective items in a batch of 525 items. This illustrates the powerful application of proportions in solving real-world problems.
Frequently Asked Questions (FAQs)
Q: Can I use a calculator to solve 40/175?
A: Yes, absolutely! A calculator provides a quick and efficient way to divide the numerator by the denominator to obtain the decimal representation. However, understanding the simplification process and converting to percentages are equally important mathematical skills.
Q: What if the numbers were larger or more complex?
A: The same principles apply regardless of the size or complexity of the numbers. The process of finding the GCD, converting to percentages or decimals, and applying proportions remains consistent. Using prime factorization or the Euclidean algorithm for larger numbers might be necessary to simplify the fraction efficiently.
Q: Are there other ways to represent this proportion?
A: Yes. Besides the fraction, percentage, and decimal representation, the proportion could also be depicted visually using a pie chart or bar graph. Visual representation can enhance the understanding of the proportion, particularly for those who are visual learners.
Conclusion: Mastering Fractions for a Brighter Future
Understanding the fraction "40 of 175," its simplification, conversion into percentages and decimals, and its real-world applications are crucial for building a strong foundation in mathematics. This knowledge isn’t confined to the classroom; it’s a valuable skill that empowers individuals to navigate various aspects of life, from financial planning to scientific endeavors. By mastering the art of working with fractions, you equip yourself with a versatile tool for effective problem-solving and a clearer understanding of the world around you. The seemingly simple fraction 40/175 opens the door to a deeper appreciation of mathematical principles and their profound relevance in everyday life. Keep practicing, explore different methods, and confidently tackle any fractional challenge that comes your way!
Latest Posts
Latest Posts
-
Fraction Of 1 75
Sep 21, 2025
-
66f To Celsius
Sep 21, 2025
-
Pint To Milliliter
Sep 21, 2025
-
5 X 17
Sep 21, 2025
-
66 To Feet
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 175 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.